Binomial heap
Encyclopedia
In computer science
, a binomial heap is a heap
similar to a binary heap
but also supports quickly merging two heaps. This is achieved by using a special tree structure. It is important as an implementation of the mergeable heap abstract data type
(also called meldable heap), which is a priority queue
supporting merge operation.
trees (compare with a binary heap
, which has a shape of a single binary tree
). A binomial tree is defined recursively:
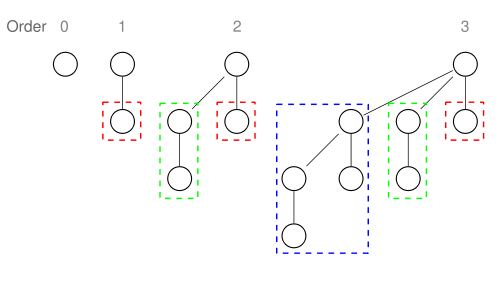A binomial tree of order k has 2k nodes, height k.
Because of its unique structure, a binomial tree of order k can be constructed from two trees of order k−1 trivially by attaching one of them as the leftmost child of root of the other one. This feature is central to the merge operation of a binomial heap, which is its major advantage over other conventional heaps.
The name comes from the shape: a binomial tree of order
has 
nodes at depth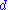 
. (See Binomial coefficient
.)
The first property ensures that the root of each binomial tree contains the smallest key in the tree, which applies to the entire heap.
The second property implies that a binomial heap with n nodes consists of at most log
n + 1 binomial trees. In fact, the number and orders of these trees are uniquely determined by the number of nodes n: each binomial tree corresponds to one digit in the binary
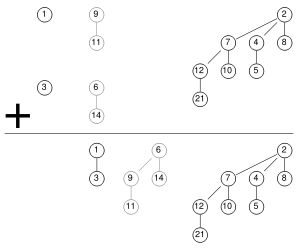
representation of number n. For example number 13 is 1101 in binary,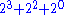
, and thus a binomial heap with 13 nodes will consist of three binomial trees of orders 3, 2, and 0 (see figure below).
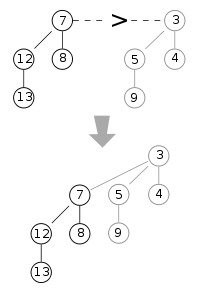
Example of a binomial heap containing 13 nodes with distinct keys.
The heap consists of three binomial trees with orders 0, 2, and 3.
, ordered by increasing order of the tree.
function mergeTree(p, q)
if p.root.key <= q.root.key
return p.addSubTree(q)
else
return q.addSubTree(p)
The operation of merging two heaps is perhaps the most interesting and can be used as a subroutine in most other operations. The lists of roots of both heaps are traversed simultaneously, similarly as in the merge algorithm
.
If only one of the heaps contains a tree of order j, this tree is moved to the merged heap. If both heaps contain a tree of order j, the two trees are merged to one tree of order j+1 so that the minimum-heap property is satisfied. Note that it may later be necessary to merge this tree with some other tree of order j+1 present in one of the heaps. In the course of the algorithm, we need to examine at most three trees of any order (two from the two heaps we merge and one composed of two smaller trees).
Because each binomial tree in a binomial heap corresponds to a bit in the binary representation of its size, there is an analogy between the merging of two heaps and the binary addition of the sizes of the two heaps, from right-to-left. Whenever a carry occurs during addition, this corresponds to a merging of two binomial trees during the merge.
Each tree has order at most log n and therefore the running time is O(log n).
function merge(p, q)
while not( p.end and q.end )
tree = mergeTree(p.currentTree, q.currentTree)
if not heap.currentTree.empty
tree = mergeTree(tree, heap.currentTree)
heap.addTree(tree)
else
heap.addTree(tree)
heap.next p.next q.next
By using a pointer to the binomial tree that contains the minimum element, the time for this operation can be reduced to O(1). The pointer must be updated when performing any operation other than Find minimum. This can be done in O(log n) without raising the running time of any operation.
function deleteMin(heap)
min = heap.trees.first
for each current in heap.trees
if current.root < min then min = current
for each tree in min.subTrees
tmp.addTree(tree)
heap.removeTree(min)
merge(heap, tmp)
(log n) time on a binomial heap with n elements:
Finding the element with minimum key can also be done in O(1) by using an additional pointer to the minimum.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a binomial heap is a heap
Heap (data structure)
In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if B is a child node of A, then key ≥ key. This implies that an element with the greatest key is always in the root node, and so such a heap is sometimes called a max-heap...
similar to a binary heap
Binary heap
A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of...
but also supports quickly merging two heaps. This is achieved by using a special tree structure. It is important as an implementation of the mergeable heap abstract data type
Abstract data type
In computing, an abstract data type is a mathematical model for a certain class of data structures that have similar behavior; or for certain data types of one or more programming languages that have similar semantics...
(also called meldable heap), which is a priority queue
Priority queue
A priority queue is an abstract data type in computer programming.It is exactly like a regular queue or stack data structure, but additionally, each element is associated with a "priority"....
supporting merge operation.
Binomial tree
A binomial heap is implemented as a collection of binomialBinomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
trees (compare with a binary heap
Binary heap
A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of...
, which has a shape of a single binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
). A binomial tree is defined recursively:
- A binomial tree of order 0 is a single node
- A binomial tree of order k has a root node whose children are roots of binomial trees of orders k−1, k−2, ..., 2, 1, 0 (in this order).
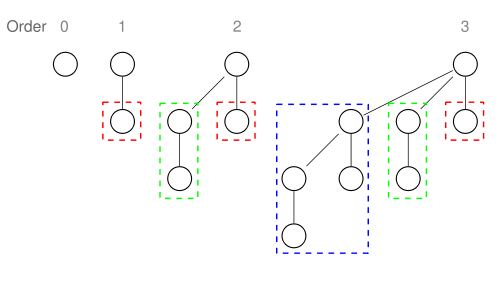
Because of its unique structure, a binomial tree of order k can be constructed from two trees of order k−1 trivially by attaching one of them as the leftmost child of root of the other one. This feature is central to the merge operation of a binomial heap, which is its major advantage over other conventional heaps.
The name comes from the shape: a binomial tree of order
has nodes at depth 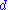. (See Binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.)
Structure of a binomial heap
A binomial heap is implemented as a set of binomial trees that satisfy the binomial heap properties:- Each binomial tree in a heap obeys the minimum-heap property: the key of a node is greater than or equal to the key of its parent.
- There can only be either one or zero binomial trees for each order, including zero order.
The first property ensures that the root of each binomial tree contains the smallest key in the tree, which applies to the entire heap.
The second property implies that a binomial heap with n nodes consists of at most log
Binary logarithm
In mathematics, the binary logarithm is the logarithm to the base 2. It is the inverse function of n ↦ 2n. The binary logarithm of n is the power to which the number 2 must be raised to obtain the value n. This makes the binary logarithm useful for anything involving powers of 2,...
n + 1 binomial trees. In fact, the number and orders of these trees are uniquely determined by the number of nodes n: each binomial tree corresponds to one digit in the binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
representation of number n. For example number 13 is 1101 in binary,
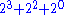, and thus a binomial heap with 13 nodes will consist of three binomial trees of orders 3, 2, and 0 (see figure below).Example of a binomial heap containing 13 nodes with distinct keys.
The heap consists of three binomial trees with orders 0, 2, and 3.
Implementation
Because no operation requires random access to the root nodes of the binomial trees, the roots of the binomial trees can be stored in a linked listLinked list
In computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...
, ordered by increasing order of the tree.
Merge
As mentioned above, the simplest and most important operation is the merging of two binomial trees of the same order within two binomial heaps. Due to the structure of binomial trees, they can be merged trivially. As their root node is the smallest element within the tree, by comparing the two keys, the smaller of them is the minimum key, and becomes the new root node. Then the other tree become a subtree of the combined tree. This operation is basic to the complete merging of two binomial heaps.function mergeTree(p, q)
if p.root.key <= q.root.key
return p.addSubTree(q)
else
return q.addSubTree(p)
Merge algorithm
Merge algorithms are a family of algorithms that run sequentially over multiple sorted lists, typically producing more sorted lists as output. This is well-suited for machines with tape drives...
.
If only one of the heaps contains a tree of order j, this tree is moved to the merged heap. If both heaps contain a tree of order j, the two trees are merged to one tree of order j+1 so that the minimum-heap property is satisfied. Note that it may later be necessary to merge this tree with some other tree of order j+1 present in one of the heaps. In the course of the algorithm, we need to examine at most three trees of any order (two from the two heaps we merge and one composed of two smaller trees).
Because each binomial tree in a binomial heap corresponds to a bit in the binary representation of its size, there is an analogy between the merging of two heaps and the binary addition of the sizes of the two heaps, from right-to-left. Whenever a carry occurs during addition, this corresponds to a merging of two binomial trees during the merge.
Each tree has order at most log n and therefore the running time is O(log n).
function merge(p, q)
while not( p.end and q.end )
tree = mergeTree(p.currentTree, q.currentTree)
if not heap.currentTree.empty
tree = mergeTree(tree, heap.currentTree)
heap.addTree(tree)
else
heap.addTree(tree)
heap.next p.next q.next
Insert
Inserting a new element to a heap can be done by simply creating a new heap containing only this element and then merging it with the original heap. Due to the merge, insert takes O(log n) time,however it has an amortized time of O(1) (i.e. constant).Find minimum
To find the minimum element of the heap, find the minimum among the roots of the binomial trees. This can again be done easily in O(log n) time, as there are just O(log n) trees and hence roots to examine.By using a pointer to the binomial tree that contains the minimum element, the time for this operation can be reduced to O(1). The pointer must be updated when performing any operation other than Find minimum. This can be done in O(log n) without raising the running time of any operation.
Delete minimum
To delete the minimum element from the heap, first find this element, remove it from its binomial tree, and obtain a list of its subtrees. Then transform this list of subtrees into a separate binomial heap by reordering them from smallest to largest order. Then merge this heap with the original heap. Since each tree has at most log n children, creating this new heap is O(log n). Merging heaps is O(log n), so the entire delete minimum operation is O(log n).function deleteMin(heap)
min = heap.trees.first
for each current in heap.trees
if current.root < min then min = current
for each tree in min.subTrees
tmp.addTree(tree)
heap.removeTree(min)
merge(heap, tmp)
Decrease key
After decreasing the key of an element, it may become smaller than the key of its parent, violating the minimum-heap property. If this is the case, exchange the element with its parent, and possibly also with its grandparent, and so on, until the minimum-heap property is no longer violated. Each binomial tree has height at most log n, so this takes O(log n) time.Delete
To delete an element from the heap, decrease its key to negative infinity (that is, some value lower than any element in the heap) and then delete the minimum in the heap.Performance
All of the following operations work in OBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(log n) time on a binomial heap with n elements:
- Insert a new element to the heap
- Find the element with minimum key
- Delete the element with minimum key from the heap
- Decrease key of a given element
- Delete given element from the heap
- Merge two given heaps to one heap
Finding the element with minimum key can also be done in O(1) by using an additional pointer to the minimum.
External links
- Java applet simulation of binomial heap
- Python implementation of binomial heap
- Two C implementations of binomial heap (a generic one and one optimized for integer keys)
- Haskell implementation of binomial heap
- Common Lisp implementation of binomial heap