
Dirichlet's theorem on arithmetic progressions
Encyclopedia
In number theory
, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime
integer
s a and d, there are infinitely many primes
of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are congruent
to a modulo
d. The numbers of the form a + nd form an arithmetic progression

and Dirichlet's theorem states that this sequence contains infinitely many prime numbers. The theorem extends Euclid's theorem
that there are infinitely many prime numbers. Stronger forms of Dirichlet's theorem state that, for any arithmetic progression, the sum of the reciprocals
of the prime numbers in the progression diverges, and that different arithmetic progressions with the same modulus have approximately the same proportions of primes. Equivalently, the primes are evenly distributed (asymptotically) among each congruence class modulo d.
Note that Dirichlet's theorem does not require the prime numbers in an arithmetic sequence to be consecutive. It is also known that there exist arbitrarily long finite arithmetic progressions consisting only of primes
, but this is a different result, known as the Green–Tao theorem.
s if it is a prime number (in the normal sense) that is congruent to 3 modulo 4.
The primes of the type 4n + 3 are
They correspond to the following values of n:
The strong form of Dirichlet's theorem implies that
is a divergent series
.
The following table lists several arithmetic progressions and the first few prime numbers in each of them.
, the same must be true for the primes in arithmetic progressions. One naturally then asks about the way the primes are shared between the various arithmetic progressions for a given value of d (there are d of those, essentially, if we don't distinguish two progressions sharing almost all
their terms). The answer is given in this form: the number of feasible progressions modulo d — those where a and d do not have a common factor > 1 — is given by Euler's totient function
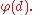
Further, the proportion of primes in each of those is
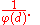
For example if d is a prime number q, each of the q − 1 progressions, other than

contains a proportion 1/(q − 1) of the primes.
When compared to each other, progressions with a quadratic nonresidue remainder have typically slightly more elements than those with a quadratic residue remainder (Chebyshev's bias
).
stated that every arithmetic progression beginning with 1 contains an infinite number of primes. The theorem in the above form was first conjectured by Legendre
in his attempted unsuccessful proofs of quadratic reciprocity
and proved by Dirichlet
in with Dirichlet L-series. The proof is modeled on Euler's earlier work relating the Riemann zeta function to the distribution of primes. The theorem represents the beginning of rigorous analytic number theory
.
gave an elementary proof
.
generalizes Dirichlet's theorem to higher-order polynomials. Whether or not even simple quadratic polynomials such as attain infinitely many prime values is an important open problem
attain infinitely many prime values is an important open problem
.
In algebraic number theory
, Dirichlet's theorem generalizes to Chebotarev's density theorem
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s a and d, there are infinitely many primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are congruent
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
to a modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
d. The numbers of the form a + nd form an arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...

and Dirichlet's theorem states that this sequence contains infinitely many prime numbers. The theorem extends Euclid's theorem
Euclid's theorem
Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. There are several well-known proofs of the theorem.-Euclid's proof:...
that there are infinitely many prime numbers. Stronger forms of Dirichlet's theorem state that, for any arithmetic progression, the sum of the reciprocals
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the prime numbers in the progression diverges, and that different arithmetic progressions with the same modulus have approximately the same proportions of primes. Equivalently, the primes are evenly distributed (asymptotically) among each congruence class modulo d.
Note that Dirichlet's theorem does not require the prime numbers in an arithmetic sequence to be consecutive. It is also known that there exist arbitrarily long finite arithmetic progressions consisting only of primes
Primes in arithmetic progression
In number theory, the phrase primes in arithmetic progression refers to at least three prime numbers that are consecutive terms in an arithmetic progression, for example the primes ....
, but this is a different result, known as the Green–Tao theorem.
Examples
An integer is a prime for the Gaussian integerGaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s if it is a prime number (in the normal sense) that is congruent to 3 modulo 4.
The primes of the type 4n + 3 are
- 3, 7, 11, 19, 23, 31, 43, 47, 59, 67, ….
They correspond to the following values of n:
- 0, 1, 2, 4, 5, 7, 10, 11, 14, 16, 17, 19, 20, 25, 26, 31, 32, 34, 37, 40, 41, 44, 47, 49, 52, 55, 56, 59, 62, 65, 67, 70, 76, 77, 82, 86, 89, 91, 94, 95, ….
The strong form of Dirichlet's theorem implies that

is a divergent series
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
.
The following table lists several arithmetic progressions and the first few prime numbers in each of them.
| Arithmetic progression | First 10 of infinitely many primes | OEIS On-Line Encyclopedia of Integer Sequences The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs... sequence |
|---|---|---|
| 2n + 1 | 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, … | |
| 4n + 1 | 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, … | |
| 4n + 3 | 3, 7, 11, 19, 23, 31, 43, 47, 59, 67, … | |
| 6n + 1 | 7, 13, 19, 31, 37, 43, 61, 67, 73, 79, … | |
| 6n + 5 | 5, 11, 17, 23, 29, 41, 47, 53, 59, 71, … | |
| 8n + 1 | 17, 41, 73, 89, 97, 113, 137, 193, 233, 241, … | |
| 8n + 3 | 3, 11, 19, 43, 59, 67, 83, 107, 131, 139, … | |
| 8n + 5 | 5, 13, 29, 37, 53, 61, 101, 109, 149, 157, … | |
| 8n + 7 | 7, 23, 31, 47, 71, 79, 103, 127, 151, 167, … | |
| 10n + 1 | 11, 31, 41, 61, 71, 101, 131, 151, 181, 191, … | |
| 10n + 3 | 3, 13, 23, 43, 53, 73, 83, 103, 113, 163, … | |
| 10n + 7 | 7, 17, 37, 47, 67, 97, 107, 127, 137, 157, … | |
| 10n + 9 | 19, 29, 59, 79, 89, 109, 139, 149, 179, 199, … |
Distribution
Since the primes thin out, on average, in accordance with the prime number theoremPrime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, the same must be true for the primes in arithmetic progressions. One naturally then asks about the way the primes are shared between the various arithmetic progressions for a given value of d (there are d of those, essentially, if we don't distinguish two progressions sharing almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
their terms). The answer is given in this form: the number of feasible progressions modulo d — those where a and d do not have a common factor > 1 — is given by Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
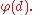
Further, the proportion of primes in each of those is
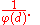
For example if d is a prime number q, each of the q − 1 progressions, other than

contains a proportion 1/(q − 1) of the primes.
When compared to each other, progressions with a quadratic nonresidue remainder have typically slightly more elements than those with a quadratic residue remainder (Chebyshev's bias
Chebyshev's bias
In prime number theory, Chebyshev's bias is the phenomenon that most of the time, there are more primes of the form 4k + 3 than of the form 4k + 1, up to the same limit. This phenomenon was first observed by Chebyshev in 1853....
).
History
EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
stated that every arithmetic progression beginning with 1 contains an infinite number of primes. The theorem in the above form was first conjectured by Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
in his attempted unsuccessful proofs of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
and proved by Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
in with Dirichlet L-series. The proof is modeled on Euler's earlier work relating the Riemann zeta function to the distribution of primes. The theorem represents the beginning of rigorous analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
.
gave an elementary proof
Elementary proof
In mathematics, an elementary proof is a mathematical proof that only uses basic techniques. More specifically, the term is used in number theory to refer to proofs that make no use of complex analysis. For some time it was thought that certain theorems, like the prime number theorem, could only be...
.
Generalizations
The Bunyakovsky conjectureBunyakovsky conjecture
The Bunyakovsky conjecture stated in 1857 by the Russian mathematician Viktor Bunyakovsky, claims that an irreducible polynomial of degree two or higher with integer coefficients generates for natural arguments either an infinite set of numbers with greatest common divisor exceeding unity, or...
generalizes Dirichlet's theorem to higher-order polynomials. Whether or not even simple quadratic polynomials such as
 attain infinitely many prime values is an important open problem
attain infinitely many prime values is an important open problemOpen problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
.
In algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, Dirichlet's theorem generalizes to Chebotarev's density theorem
Chebotarev's density theorem
Chebotarev's density theorem in algebraic number theory describes statistically the splitting of primes in a given Galois extension K of the field Q of rational numbers. Generally speaking, a prime integer will factor into several ideal primes in the ring of algebraic integers of K. There are only...
.
See also
- Linnik's theoremLinnik's theoremLinnik's theorem in analytic number theory answers a natural question after Dirichlet's theorem on arithmetic progressions. It asserts that, if we denote p the least prime in the arithmetic progressiona + nd,\...
(1944) - Bombieri–Vinogradov theoremBombieri–Vinogradov theoremIn mathematics, the Bombieri–Vinogradov theorem is a major result of analytic number theory, obtained in the mid-1960s. The first result of this kind was obtained by Barban in 1961 and the Bombieri–Vinogradov theorem is a refinement of Barban's result. The Bombieri-Vinogradov theorem is named...
- Brun–Titchmarsh theoremBrun–Titchmarsh theoremIn analytic number theory, the Brun–Titchmarsh theorem, named after Viggo Brun and Edward Charles Titchmarsh, is an upper bound on the distribution of prime numbers in arithmetic progression...
- Siegel–Walfisz theorem
- Dirichlet's approximation theoremDirichlet's approximation theoremIn number theory, Dirichlet's theorem on Diophantine approximation, also called Dirichlet's approximation theorem, states that for any real number α and any positive integer N, there exists integers p and q such that 1 ≤ q ≤ N and...
External links
- Scans of the original paper in German
- Dirichlet: There are infinitely many prime numbers in all arithmetic progressions with first term and difference coprime English translation of the original paper at the arXiv
- Dirichlet's Theorem by Jay Warendorff, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.

