
Differentiation under the integral sign
Encyclopedia
Differentiation under the integral sign is a useful operation in calculus
. Suppose that it is required to differentiate with respect to x the function
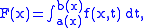
where the functions and
and 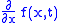 are both continuous in both
are both continuous in both  and
and  in some region of the
in some region of the 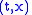 plane, including
plane, including 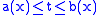 ,
, 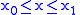 , and the functions
, and the functions 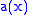 and
and  are both continuous and both have continuous derivatives for
are both continuous and both have continuous derivatives for  . Then for
. Then for 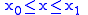 :
:
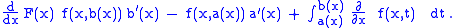
This formula is the general form of the Leibniz integral rule
and can be derived using the
fundamental theorem of calculus
. The fundamental theorem of calculus is just a particular case of the above formula, for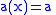 , a constant,
, a constant,  and
and 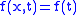 .
.
If both upper and lower limits are taken as constants, then the formula takes the shape of an operator equation:

where is the partial derivative
is the partial derivative
with respect to and
and 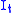 is the integral operator with respect to
is the integral operator with respect to  over a fixed interval
over a fixed interval
. That is, it is related to the symmetry of second derivatives
, but involving integrals as well as derivatives. This case is also known as the Leibniz integral rule
.
The following three basic theorems on the interchange of limits
are essentially equivalent:
as the Reynolds transport theorem
:

where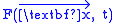 is a scalar function,
is a scalar function, 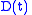 and
and 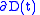 denote a time-varying connected region of
denote a time-varying connected region of 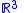 and its boundary, respectively,
and its boundary, respectively, 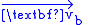 is the Eulerian velocity of the boundary (see Lagrangian and Eulerian coordinates
is the Eulerian velocity of the boundary (see Lagrangian and Eulerian coordinates
) and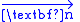 is unit outwards normal.
is unit outwards normal.
The general statement of the Leibniz integral rule requires concepts from differential geometry
, specifically differential forms, exterior derivative
s, wedge products and interior products. With those tools, the Leibniz integral rule in -dimensions is:
-dimensions is:
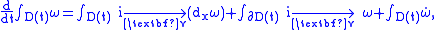
where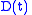 is a time-varying domain of integration,
is a time-varying domain of integration,  is a
is a  -form,
-form, 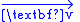 is the vector field of the velocity,
is the vector field of the velocity, 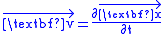 ,
, 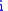 denotes the interior product,
denotes the interior product, 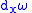 is the exterior derivative
is the exterior derivative
of with respect to the space variables only and
with respect to the space variables only and  is the time-derivative of
is the time-derivative of 
 and its lower limit
and its lower limit 
If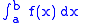 is a continuous function
is a continuous function
of or
or  , then, from the definition of the definite integral,
, then, from the definition of the definite integral, 
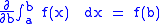 and
and 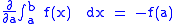
since, from proof of the fundamental theorem of calculus,
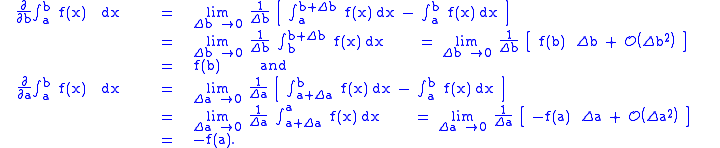
Suppose and
and  are constant, and that
are constant, and that 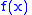 involves a parameter
involves a parameter  which is constant in the integration but may vary to form different integrals. Then, by the definition of a function,
which is constant in the integration but may vary to form different integrals. Then, by the definition of a function,
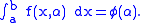
In general, this may be differentiated by differentiating under the integral sign; i.e.,
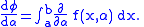
To prove this and, at the same time, to determine conditions under which the formula is true, we proceed as follows:
From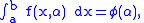
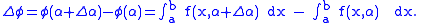
From the fact that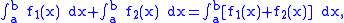 we have
we have
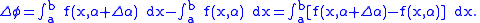
If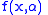 is a continuous function of
is a continuous function of  and
and 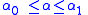 when
when 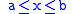 then for any
then for any  there exists
there exists 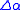 such that
such that
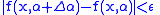 for all values of
for all values of 
(This follows from the Heine–Cantor theorem
that every continuous function on a compact set is uniformly continuous.)
Therefore, from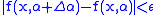 and
and 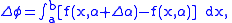
we get
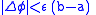
and the fact that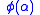 is, therefore, a continuous function.
is, therefore, a continuous function.
Similarly if exists and is continuous, then for all
exists and is continuous, then for all  there exists
there exists 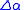 such that:
such that:
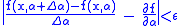 for all
for all 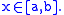
Therefore,
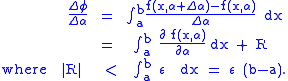
Now,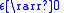 as
as 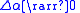 , therefore,
, therefore,
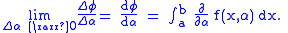
This is the formula we set out to prove.
Now, suppose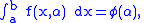 where
where  and
and  are functions of
are functions of  which take increments
which take increments 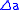 and
and 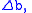 respectively, when
respectively, when  is increased by
is increased by  Then,
Then,

A form of the mean value theorem
,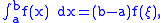 where
where 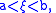 can be applied to the first and last integrals of the formula for
can be applied to the first and last integrals of the formula for 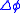 above, resulting in
above, resulting in
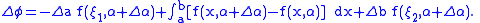
Dividing by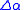 , letting
, letting 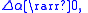 noticing
noticing  and
and 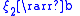 and using the result
and using the result 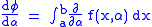 yields
yields

This is the general form of the Leibniz integral rule
.
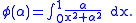
If

If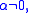

The function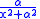 is not continuous at the point
is not continuous at the point 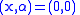 and the function
and the function 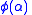 has a discontinuity at
has a discontinuity at  because
because 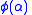 approaches
approaches 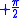 as
as 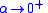 and approaches
and approaches 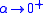 as
as 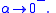
If we now differentiate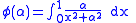 with respect to
with respect to  under the integral sign, we get
under the integral sign, we get
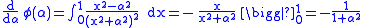 ,
,
which is, of course, true for all values of except
except 
Consider integrating
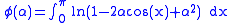
(for ).
).
Now,
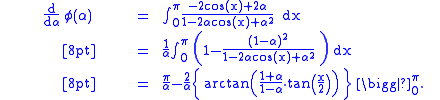
As varies from
varies from  to
to 
 varies through positive values from
varies through positive values from  to
to  when
when  and
and  varies through negative values from
varies through negative values from  to
to  when
when 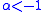 or
or 
Hence,
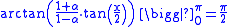 when
when 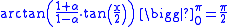
and
 when
when 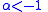 or
or 
Therefore,
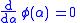 when
when 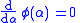 and
and
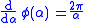 when
when  or
or 
Upon integrating both sides with respect to , we get
, we get  when
when 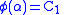 and
and 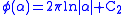 when
when 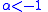 or
or 
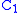 may be determined by setting
may be determined by setting  in
in
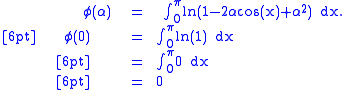
Thus, Hence,
Hence, 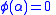 when
when 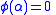
To determine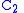 in the same manner, we should need to substitute in
in the same manner, we should need to substitute in  a value of
a value of  greater numerically than 1. This is somewhat inconvenient. Instead, we substitute
greater numerically than 1. This is somewhat inconvenient. Instead, we substitute 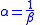 , where
, where 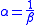 Then,
Then,
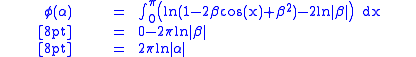
Therefore, (and
(and 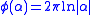 when
when 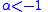 or
or  )
)
The definition of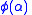 is now complete:
is now complete:
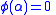 when
when 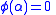 and
and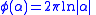 when
when 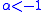 or
or 
The foregoing discussion, of course, does not apply when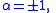 since the conditions for differentiability are not met.
since the conditions for differentiability are not met.
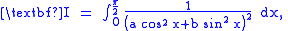
where both , by differentiating under the integral sign.
, by differentiating under the integral sign.
Let us first find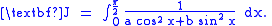
Dividing both the numerator and the denominator by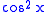 yields
yields
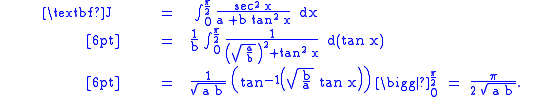
The limits of integration being independent of
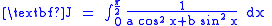 gives us
gives us
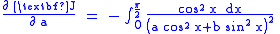
whereas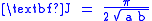 gives us
gives us
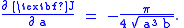
Equating these two relations then yields
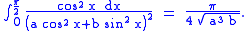
In a similar fashion, pursuing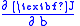 yields
yields
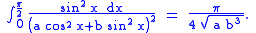
Adding the two results then produces

which is the value of the integral
Note that if we define
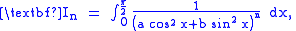
it can easily be shown that
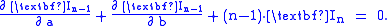
Given this partial-derivative-based recursive relation (i.e., integral reduction formula) can then be utilized to compute all of the values of
this partial-derivative-based recursive relation (i.e., integral reduction formula) can then be utilized to compute all of the values of 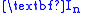 for
for  (
(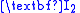 ,
,  ,
, 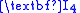 etc.).
etc.).
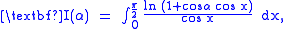
for
Differentiating under the integral with respect to we have
we have
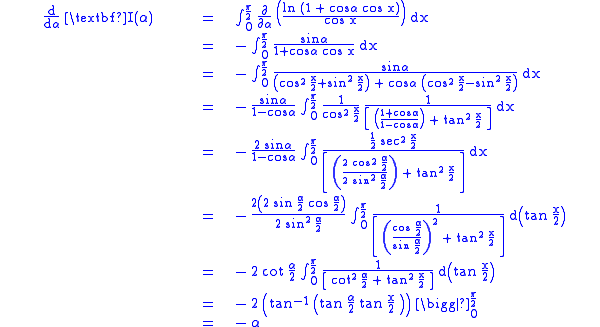
Now, when , we have, from
, we have, from 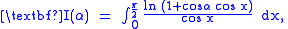
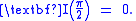
Hence,

which is the value of the integral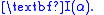
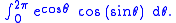
We introduce a new variable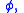 and rewrite the integral as
and rewrite the integral as
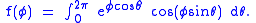
Note that for

Thus, we proceed
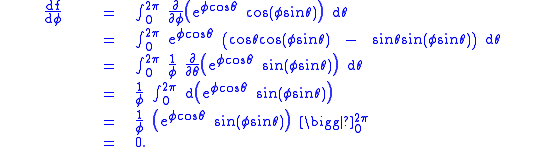
From the equation for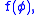 we can see
we can see 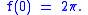 So, integrating both sides of
So, integrating both sides of  with respect to
with respect to  between the limits
between the limits  and
and 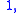 yields
yields
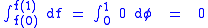



which is the value of the integral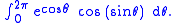
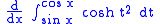 . In this example, we shall simply apply the above given formula, to get
. In this example, we shall simply apply the above given formula, to get
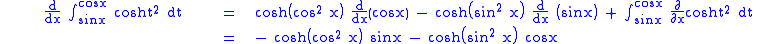
where the derivative with respect to x of hyperbolic cosine t squared is 0. This is a simple example on how to use this formula for variable limits.
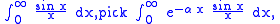

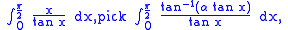
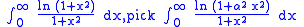
and for
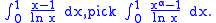
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. Suppose that it is required to differentiate with respect to x the function
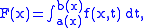
where the functions
 and
and 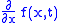 are both continuous in both
are both continuous in both  and
and  in some region of the
in some region of the 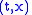 plane, including
plane, including 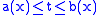 ,
, 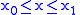 , and the functions
, and the functions 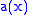 and
and  are both continuous and both have continuous derivatives for
are both continuous and both have continuous derivatives for  . Then for
. Then for 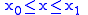 :
: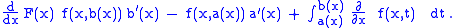
This formula is the general form of the Leibniz integral rule
Leibniz integral rule
In mathematics, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz, tells us that if we have an integral of the formthen for x \in the derivative of this integral is thus expressible...
and can be derived using the
fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
. The fundamental theorem of calculus is just a particular case of the above formula, for
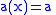 , a constant,
, a constant,  and
and 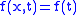 .
.If both upper and lower limits are taken as constants, then the formula takes the shape of an operator equation:

where
 is the partial derivative
is the partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
with respect to
 and
and 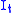 is the integral operator with respect to
is the integral operator with respect to  over a fixed interval
over a fixed intervalInterval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
. That is, it is related to the symmetry of second derivatives
Symmetry of second derivatives
In mathematics, the symmetry of second derivatives refers to the possibility of interchanging the order of taking partial derivatives of a functionfof n variables...
, but involving integrals as well as derivatives. This case is also known as the Leibniz integral rule
Leibniz integral rule
In mathematics, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz, tells us that if we have an integral of the formthen for x \in the derivative of this integral is thus expressible...
.
The following three basic theorems on the interchange of limits
Interchange of limiting operations
In mathematics, the study of interchange of limiting operations is one of the major concerns of mathematical analysis. in that two given limiting operations, say L and M, cannot be assumed to give the same result when applied in either order...
are essentially equivalent:
- the interchange of a derivative and an integral (differentiation under the integral sign; i.e., Leibniz integral ruleLeibniz integral ruleIn mathematics, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz, tells us that if we have an integral of the formthen for x \in the derivative of this integral is thus expressible...
) - the change of order of partial derivatives
- the change of order of integration (integration under the integral sign; i.e., Fubini's theoremFubini's theoremIn mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
)
Higher dimensions
The Leibniz integral rule can be extended to multidimensional integrals. In two and three dimensions, this rule is better known from the field of fluid dynamicsFluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
as the Reynolds transport theorem
Reynolds transport theorem
Reynolds' transport theorem , or in short Reynolds theorem, is a three-dimensional generalization of the Leibniz integral rule which is also known as differentiation under the integral sign....
:

where
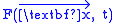 is a scalar function,
is a scalar function, 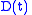 and
and 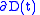 denote a time-varying connected region of
denote a time-varying connected region of 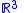 and its boundary, respectively,
and its boundary, respectively, 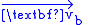 is the Eulerian velocity of the boundary (see Lagrangian and Eulerian coordinates
is the Eulerian velocity of the boundary (see Lagrangian and Eulerian coordinatesLagrangian and Eulerian coordinates
In fluid dynamics and finite-deformation plasticity the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the...
) and
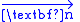 is unit outwards normal.
is unit outwards normal.The general statement of the Leibniz integral rule requires concepts from differential geometry
Differential geometry and topology
Differential geometry is a mathematical discipline that uses the techniques of differential and integral calculus, as well as linear and multilinear algebra, to study problems in geometry. The theory of plane and space curves and of surfaces in the three-dimensional Euclidean space formed the basis...
, specifically differential forms, exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
s, wedge products and interior products. With those tools, the Leibniz integral rule in
 -dimensions is:
-dimensions is: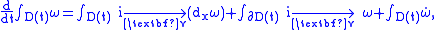
where
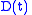 is a time-varying domain of integration,
is a time-varying domain of integration,  is a
is a  -form,
-form, 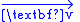 is the vector field of the velocity,
is the vector field of the velocity, 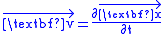 ,
, 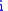 denotes the interior product,
denotes the interior product, 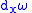 is the exterior derivative
is the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of
 with respect to the space variables only and
with respect to the space variables only and  is the time-derivative of
is the time-derivative of 
Derivation of the principle of differentiation under the integral sign
A definite integral is a function of its upper limit and its lower limit
and its lower limit 
If
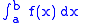 is a continuous function
is a continuous functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of
 or
or  , then, from the definition of the definite integral,
, then, from the definition of the definite integral, 
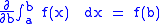 and
and 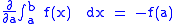
since, from proof of the fundamental theorem of calculus,
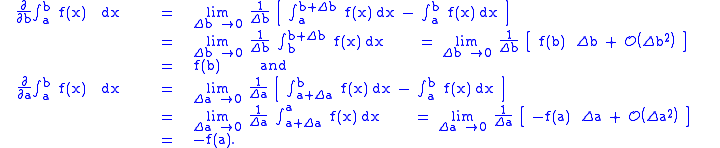
Suppose
 and
and  are constant, and that
are constant, and that 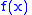 involves a parameter
involves a parameter  which is constant in the integration but may vary to form different integrals. Then, by the definition of a function,
which is constant in the integration but may vary to form different integrals. Then, by the definition of a function,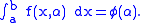
In general, this may be differentiated by differentiating under the integral sign; i.e.,
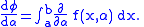
To prove this and, at the same time, to determine conditions under which the formula is true, we proceed as follows:
From
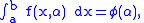
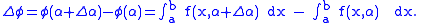
From the fact that
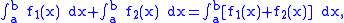 we have
we have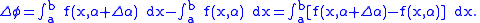
If
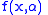 is a continuous function of
is a continuous function of  and
and 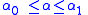 when
when 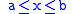 then for any
then for any  there exists
there exists 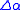 such that
such that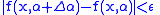 for all values of
for all values of 
(This follows from the Heine–Cantor theorem
Heine–Cantor theorem
In mathematics, the Heine–Cantor theorem, named after Eduard Heine and Georg Cantor, states that if M and N are metric spaces and M is compact then every continuous functionis uniformly continuous....
that every continuous function on a compact set is uniformly continuous.)
Therefore, from
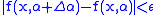 and
and 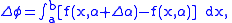
we get
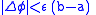
and the fact that
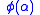 is, therefore, a continuous function.
is, therefore, a continuous function.Similarly if
 exists and is continuous, then for all
exists and is continuous, then for all  there exists
there exists 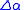 such that:
such that: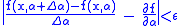 for all
for all 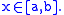
Therefore,
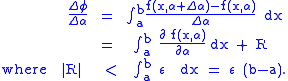
Now,
 as
as  , therefore,
, therefore,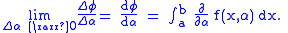
This is the formula we set out to prove.
Now, suppose
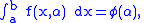 where
where  and
and  are functions of
are functions of  which take increments
which take increments 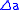 and
and 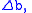 respectively, when
respectively, when  is increased by
is increased by  Then,
Then,
A form of the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
,
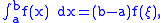 where
where 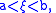 can be applied to the first and last integrals of the formula for
can be applied to the first and last integrals of the formula for 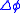 above, resulting in
above, resulting in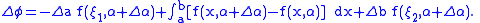
Dividing by
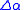 , letting
, letting 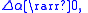 noticing
noticing  and
and 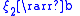 and using the result
and using the result 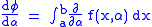 yields
yields
This is the general form of the Leibniz integral rule
Leibniz integral rule
In mathematics, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz, tells us that if we have an integral of the formthen for x \in the derivative of this integral is thus expressible...
.
Example 1
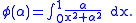
If


If
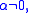

The function
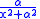 is not continuous at the point
is not continuous at the point 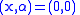 and the function
and the function 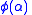 has a discontinuity at
has a discontinuity at  because
because 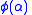 approaches
approaches 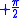 as
as 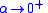 and approaches
and approaches 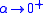 as
as 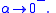
If we now differentiate
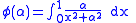 with respect to
with respect to  under the integral sign, we get
under the integral sign, we get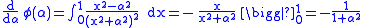 ,
,which is, of course, true for all values of
 except
except 
Example 2
The principle of differentiating under the integral sign may sometimes be used to evaluate a definite integral.Consider integrating
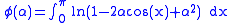
(for
 ).
).Now,
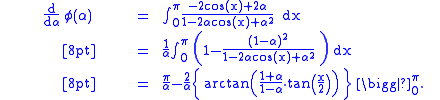
As
 varies from
varies from  to
to 
 varies through positive values from
varies through positive values from  to
to  when
when  and
and  varies through negative values from
varies through negative values from  to
to  when
when 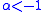 or
or 
Hence,
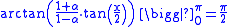 when
when 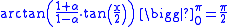
and
 when
when 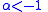 or
or 
Therefore,
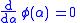 when
when 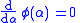 and
and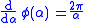 when
when  or
or 
Upon integrating both sides with respect to
 , we get
, we get  when
when 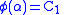 and
and 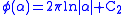 when
when 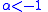 or
or 
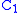 may be determined by setting
may be determined by setting  in
in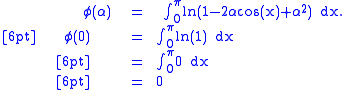
Thus,
 Hence,
Hence, 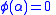 when
when 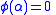
To determine
 in the same manner, we should need to substitute in
in the same manner, we should need to substitute in  a value of
a value of  greater numerically than 1. This is somewhat inconvenient. Instead, we substitute
greater numerically than 1. This is somewhat inconvenient. Instead, we substitute 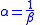 , where
, where 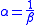 Then,
Then,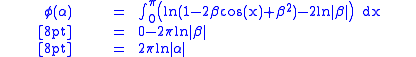
Therefore,
 (and
(and 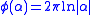 when
when 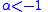 or
or  )
)The definition of
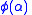 is now complete:
is now complete: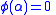 when
when 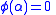 and
and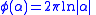 when
when 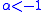 or
or 
The foregoing discussion, of course, does not apply when
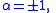 since the conditions for differentiability are not met.
since the conditions for differentiability are not met.Example 3
Here, we consider the integration of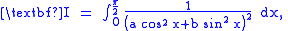
where both
 , by differentiating under the integral sign.
, by differentiating under the integral sign.Let us first find
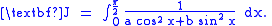
Dividing both the numerator and the denominator by
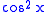 yields
yields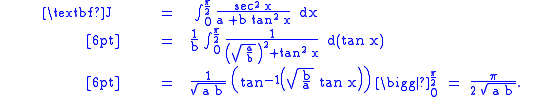
The limits of integration being independent of
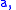
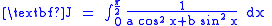 gives us
gives us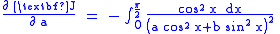
whereas
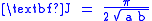 gives us
gives us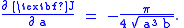
Equating these two relations then yields
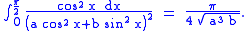
In a similar fashion, pursuing
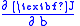 yields
yields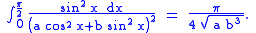
Adding the two results then produces

which is the value of the integral

Note that if we define
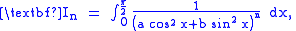
it can easily be shown that
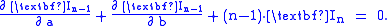
Given
 this partial-derivative-based recursive relation (i.e., integral reduction formula) can then be utilized to compute all of the values of
this partial-derivative-based recursive relation (i.e., integral reduction formula) can then be utilized to compute all of the values of 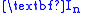 for
for  (
(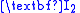 ,
,  ,
, 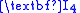 etc.).
etc.).Example 4
Here, we consider the integral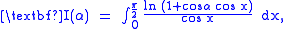
for

Differentiating under the integral with respect to
 we have
we have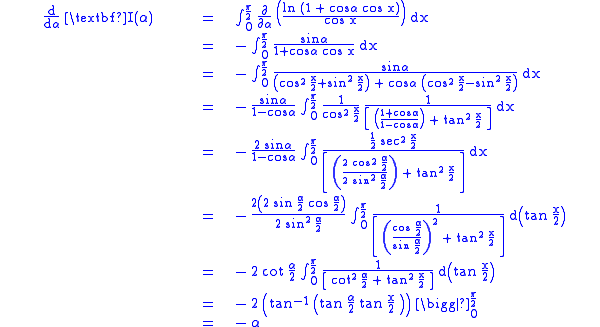
Now, when
 , we have, from
, we have, from 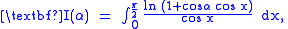
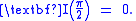
Hence,

which is the value of the integral
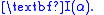
Example 5
Here, we consider the integral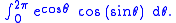
We introduce a new variable
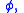 and rewrite the integral as
and rewrite the integral as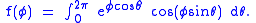
Note that for


Thus, we proceed
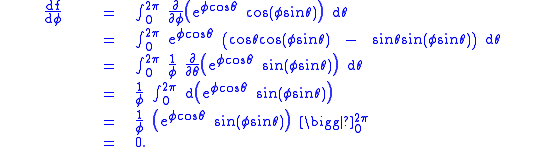
From the equation for
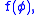 we can see
we can see 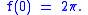 So, integrating both sides of
So, integrating both sides of  with respect to
with respect to  between the limits
between the limits  and
and  yields
yields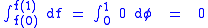



which is the value of the integral
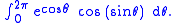
Example 6
Here is an example that has variable limits. Let us try to find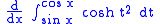 . In this example, we shall simply apply the above given formula, to get
. In this example, we shall simply apply the above given formula, to get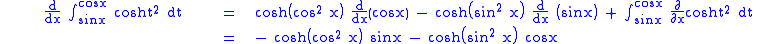
where the derivative with respect to x of hyperbolic cosine t squared is 0. This is a simple example on how to use this formula for variable limits.
Other problems
There are innumerable other integrals that can be solved "quickly" using the technique of differentiation under the integral sign. For examples, to solve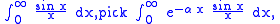

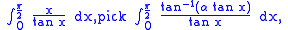
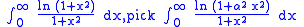
and for
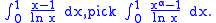
Popular culture
- Differentiation under the integral sign is mentioned in the late physicistPhysicistA physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
Richard Feynman'sRichard FeynmanRichard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
best-selling memoir Surely You're Joking, Mr. Feynman!Surely You're Joking, Mr. Feynman!"Surely You're Joking, Mr. Feynman!": Adventures of a Curious Character is an edited collection of reminiscences by the Nobel Prize-winning physicist Richard Feynman. The book, released in 1985, covers a variety of instances in Feynman's life...
(in the chapter "A Different Box of Tools"), where he mentions learning it from an old text, Advanced Calculus (1926), by Frederick S. Woods (who was a professor of mathematics in the Massachusetts Institute of TechnologyMassachusetts Institute of TechnologyThe Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...
) while in high schoolHigh schoolHigh school is a term used in parts of the English speaking world to describe institutions which provide all or part of secondary education. The term is often incorporated into the name of such institutions....
. The technique was not often taught when Feynman later received his formal education in calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and, knowing it, Feynman was able to use the technique to solve some otherwise difficult integration problems upon his arrival at graduate school at Princeton UniversityPrinceton UniversityPrinceton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
. The direct citation from Surely You're Joking, Mr. Feynman! regarding the method of differentiation under the integral sign is as follows:

