
Reynolds transport theorem
Encyclopedia
Reynolds' transport theorem (also known as the Leibniz-Reynolds' transport theorem), or in short Reynolds theorem, is a three-dimensional generalization of the Leibniz integral rule
which is also known as differentiation under the integral sign.
The theorem is named after Osborne Reynolds
(1842–1912). It is used to recast derivatives of integrated quantities and is useful in formulating the basic equations of continuum mechanics
.
Consider integrating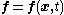 over the time-dependent region
over the time-dependent region 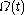 that has boundary
that has boundary 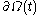 , then taking the derivative with respect time:
, then taking the derivative with respect time: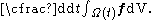
If we wish to move the derivative under the integral sign there are two issues: the time dependence of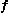 , and the introduction of and removal of space from
, and the introduction of and removal of space from  due to its dynamic boundary. Reynolds' transport theorem provides the necessary framework.
due to its dynamic boundary. Reynolds' transport theorem provides the necessary framework.
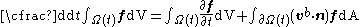
in which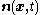 is the outward-pointing unit-normal,
is the outward-pointing unit-normal, 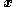 is a point in the region and is the variable of integration,
is a point in the region and is the variable of integration, 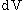 and
and 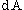 are volume and surface elements at
are volume and surface elements at 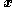 , and
, and 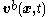 is the velocity of the area element. The function
is the velocity of the area element. The function 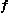 may be vector or scalar valued. Note that the integral on the left hand side is a function solely of time, and so the total derivative has been used.
may be vector or scalar valued. Note that the integral on the left hand side is a function solely of time, and so the total derivative has been used.
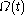 is a material element then there is a velocity function
is a material element then there is a velocity function 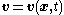 and the boundary elements obey
and the boundary elements obey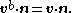
This condition may be substituted to obtain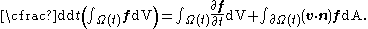
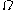 to be constant with respect to time, then
to be constant with respect to time, then 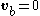 and the identity reduces to
and the identity reduces to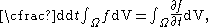
as expected. This simplification is not possible if an incorrect form of the Reynolds transport theorem is used.
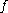 is independent of
is independent of 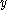 &
&  , and that
, and that 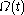 is a unit square in the
is a unit square in the 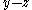 plane and has
plane and has  limits
limits 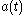 and
and 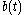 . Then Reynolds transport theorem reduces to
. Then Reynolds transport theorem reduces to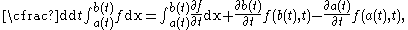
which is the expression given on Differentiation under the integral sign, except that there the variables x and t have been swapped.
Leibniz integral rule
In mathematics, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz, tells us that if we have an integral of the formthen for x \in the derivative of this integral is thus expressible...
which is also known as differentiation under the integral sign.
The theorem is named after Osborne Reynolds
Osborne Reynolds
Osborne Reynolds FRS was a prominent innovator in the understanding of fluid dynamics. Separately, his studies of heat transfer between solids and fluids brought improvements in boiler and condenser design.-Life:...
(1842–1912). It is used to recast derivatives of integrated quantities and is useful in formulating the basic equations of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
.
Consider integrating
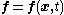 over the time-dependent region
over the time-dependent region 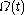 that has boundary
that has boundary 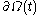 , then taking the derivative with respect time:
, then taking the derivative with respect time: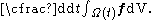
If we wish to move the derivative under the integral sign there are two issues: the time dependence of
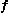 , and the introduction of and removal of space from
, and the introduction of and removal of space from  due to its dynamic boundary. Reynolds' transport theorem provides the necessary framework.
due to its dynamic boundary. Reynolds' transport theorem provides the necessary framework.General form
Reynolds' transport theorem, derived in , is: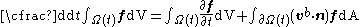
in which
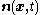 is the outward-pointing unit-normal,
is the outward-pointing unit-normal, 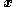 is a point in the region and is the variable of integration,
is a point in the region and is the variable of integration, 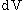 and
and 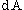 are volume and surface elements at
are volume and surface elements at 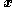 , and
, and 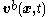 is the velocity of the area element. The function
is the velocity of the area element. The function 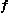 may be vector or scalar valued. Note that the integral on the left hand side is a function solely of time, and so the total derivative has been used.
may be vector or scalar valued. Note that the integral on the left hand side is a function solely of time, and so the total derivative has been used.Form for a Material Element
In continuum mechanics this theorem is often used for material elements, which are parcels of fluids or solids which no material enters or leaves. If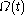 is a material element then there is a velocity function
is a material element then there is a velocity function 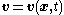 and the boundary elements obey
and the boundary elements obey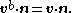
This condition may be substituted to obtain
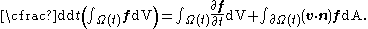
| Proof for a Material Element |
|---|
Let 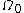 be reference configuration of the region be reference configuration of the region 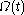 . Let . Letthe motion and the deformation gradient be given by 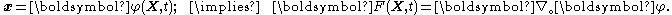 Let 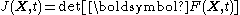 . .Then, integrals in the current and the reference configurations are related by 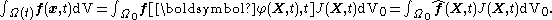 That this derivation is for a material element is implicit in the time constancy of the reference configuration: it is constant in material coordinates. The time derivative of an integral over a volume is defined as 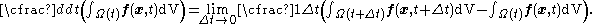 Converting into integrals over the reference configuration, we get 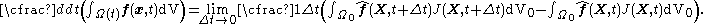 Since 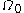 is independent of time, we have is independent of time, we have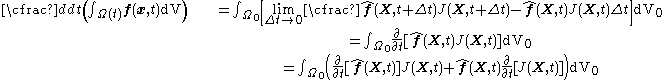 Now, the time derivative of 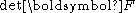 is given by is given by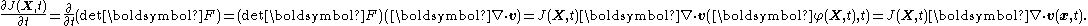 Therefore, 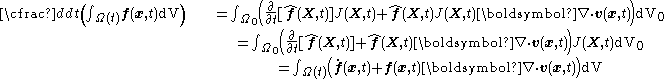 where  is the material time derivative of is the material time derivative of 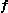 . Now, . Now,the material derivative is given by 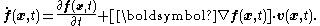 Therefore, 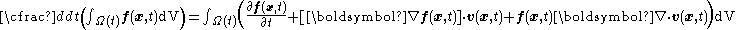 or, 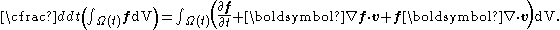 Using the identity 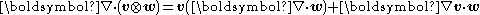 we then have 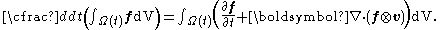 Using the divergence theorem Divergence theorem In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem... and the identity 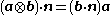 we have we have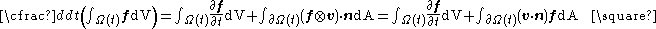 |
Erroneous sources
This theorem is widely quoted, incorrectly, as being the form specific to material volumes. See the planetmath external link below for an example. Clearly, if the material volume form is applied to regions other than material volumes, errors will ensue.A special case
If we take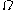 to be constant with respect to time, then
to be constant with respect to time, then 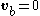 and the identity reduces to
and the identity reduces to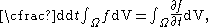
as expected. This simplification is not possible if an incorrect form of the Reynolds transport theorem is used.
Interpretation and reduction to one dimension
The theorem is the higher dimensional extension of Differentiation under the integral sign and should reduce to that expression in some cases. Suppose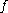 is independent of
is independent of 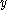 &
&  , and that
, and that 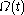 is a unit square in the
is a unit square in the 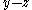 plane and has
plane and has  limits
limits 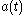 and
and 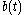 . Then Reynolds transport theorem reduces to
. Then Reynolds transport theorem reduces to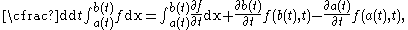
which is the expression given on Differentiation under the integral sign, except that there the variables x and t have been swapped.
External links
- Osborne Reynolds, Collected Papers on Mechanical and Physical Subjects, in three volumes, published circa 1903, now fully and freely available in digital format:

