
Heine–Cantor theorem
Encyclopedia
In mathematics
, the Heine–Cantor theorem, named after Eduard Heine
and Georg Cantor
, states that if M and N are metric spaces
and M is compact
then every continuous function
is uniformly continuous.
For instance, if f : [a,b] → R is a continuous function, then it is uniformly continuous.
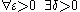 such that
such that 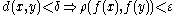 for all x, y in M
for all x, y in M
is:
 such that
such that 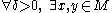 such that
such that 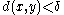 and
and 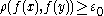
where d and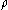 are the distance functions on metric spaces M and N, respectively.
are the distance functions on metric spaces M and N, respectively.
Choose two sequences xn and yn such that and
and 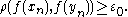
As the metric space is compact there exist
two converging subsequences ( to x0 and
to x0 and  to y0), so
to y0), so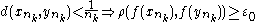
but as f is continuous and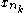 and
and 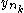 converge to the same point, this statement is impossible.
converge to the same point, this statement is impossible.
For an alternative proof in the case of a closed interval, see the article on non-standard calculus.
a closed interval, see the article on non-standard calculus.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Heine–Cantor theorem, named after Eduard Heine
Eduard Heine
Heinrich Eduard Heine was a German mathematician.Heine became known for results on special functions and in real analysis. In particular, he authored an important treatise on spherical harmonics and Legendre functions . He also investigated basic hypergeometric series...
and Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
, states that if M and N are metric spaces
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
and M is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
then every continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
- f : M → N,
is uniformly continuous.
For instance, if f : [a,b] → R is a continuous function, then it is uniformly continuous.
Proof
Suppose that f is continuous on a compact metric space M but not uniformly continuous, then the negation of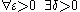 such that
such that 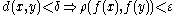 for all x, y in M
for all x, y in Mis:
 such that
such that 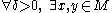 such that
such that 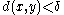 and
and 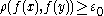
where d and
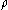 are the distance functions on metric spaces M and N, respectively.
are the distance functions on metric spaces M and N, respectively.Choose two sequences xn and yn such that
 and
and 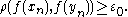
As the metric space is compact there exist
Bolzano–Weierstrass theorem
In real analysis, the Bolzano–Weierstrass theorem is a fundamental result about convergence in a finite-dimensional Euclidean space Rn. The theorem states thateach bounded sequence in Rn has a convergent subsequence...
two converging subsequences (
 to x0 and
to x0 and  to y0), so
to y0), so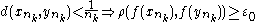
but as f is continuous and
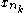 and
and 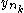 converge to the same point, this statement is impossible.
converge to the same point, this statement is impossible.For an alternative proof in the case of
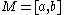 a closed interval, see the article on non-standard calculus.
a closed interval, see the article on non-standard calculus.

