
Differentiation rules
Encyclopedia
This article is a summary of the differentiation rules in elementary calculus
, i.e. rules for computing the derivative
of a function
in calculus
and mathematical analysis
.
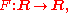

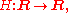
where R denotes the set of all real number
s. In some cases, they apply more generally to the set of complex numbers - provided they are well defined.
The rules given below are in the Leibniz's notation. The identities take the following form:
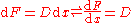
where D is the derivative. They are in this form because:
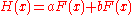
is in prime notation,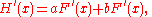
in Leibniz's notation: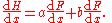
Special cases include:
of functions: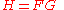
is in prime notation,
in Leibniz's notation: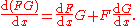
 of two functions F and G. For
of two functions F and G. For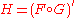
in prime notation,
in Leibniz's notation: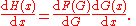
n (including zero), F is defined by
 ,
,
then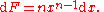
Special cases include:
Combining this rule with the linearity of the derivative allows the computation of the derivative of any polynomial.
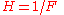
So the derivative in prime notation: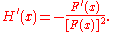
In Leibniz's notation,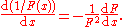
is its inverse with respect to function composition
, not with respect to the product of functions.
If the function F has an inverse G = F−1, so that G(F(x)) = x and F(G(y)) = y, then in prime notation: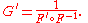
In Leibniz notation, this is written (suggestively) as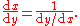
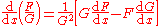
This can be derived from reciprocal rule and the product rule. Conversely (using the constant rule) the reciprocal rule is the special case F(x) = 1.
is another way of stating the rule for differentiating the logarithm of a function (using the chain rule):
wherever F is positive (since the logarithm of a negative number is undefined, and requres the complex logarithm
for evaluation).
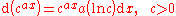
NB: The equation above is true for all c, but the derivative for c < 0 yields a complex number.
A corollary is
For the natural logarithm:
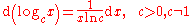
The equation above is also true for all c but yields a complex number.
Further rules: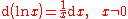
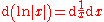

The derivative of the natural logarithm of a generalised function argument F(x) is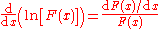
By applying the change-of-base rule, the derivative for the logarithm to a base b is: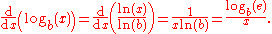
. Below y is the dependent variable, x is the independent variable, real number
constants are A, B, N, r, real integers are n and j, F(x) is a continuously differentiable function (the nth derivative exists), and i is the imaginary unit
 .
.
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, i.e. rules for computing the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
Nomenclature
- All functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
are for one realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and independant variableDependent and independent variablesThe terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
x, and continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
where specified. - Functions are denoted by F = F(x), G = G(x), H = H(x), defined by the mappings from R to R:
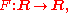

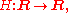
where R denotes the set of all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. In some cases, they apply more generally to the set of complex numbers - provided they are well defined.
The rules given below are in the Leibniz's notation. The identities take the following form:
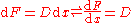
where D is the derivative. They are in this form because:
- differentiation identities can be manipulated easily:
- readily be used in integrationIntegration- Sociology and economy :*Social integration*Racial integration, refers to social and cultural behavior*Economic integration, refers to trade unification between different states*Educational integration of students with disabilities*Regional integration...
by partsIntegration by partsIn calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
or substitutionIntegration by substitutionIn calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
.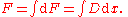
Elementary rules of differentiation
The following are basic rules of differentiation, which are used in combination to differentiate a wide variety of functions . They can be generalized to n-th orders of differentiation, and more complicated and general combinations of functions.Linearity of differentiation
The derivative of a linear combination of functions: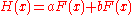
is in prime notation,
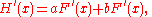
in Leibniz's notation:
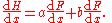
Special cases include:
- The constant multiple ruleConstant factor rule in differentiationIn calculus, the constant factor rule in differentiation, also known as The Kutz Rule, allows you to take constants outside a derivative and concentrate on differentiating the function of x itself...
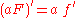
- The sum ruleSum rule in differentiationIn calculus, the sum rule in differentiation is a method of finding the derivative of a function that is the sum of two other functions for which derivatives exist. This is a part of the linearity of differentiation. The sum rule in integration follows from it...
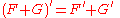
- The subtraction rule

The product or Leibniz rule
The derivative of a productProduct (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of functions:
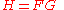
is in prime notation,

in Leibniz's notation:
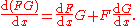
The chain rule
This is a rule for computing the derivative of a "function of a function". That is, of the compositeFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
 of two functions F and G. For
of two functions F and G. For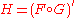
in prime notation,

in Leibniz's notation:
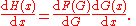
The polynomial or elementary power rule
If for some natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n (including zero), F is defined by
 ,
,then
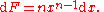
Special cases include:
- Constant rule: if F is the constant function F(x) = c, for any constant number c, then for all x

- The derivative of a linear function is constant: if F(x) = ax (or more generally, in view of the constant rule, if F(x)=ax+b ), then
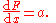
Combining this rule with the linearity of the derivative allows the computation of the derivative of any polynomial.
The reciprocal rule
This is the derivative of the reciprocal of a function F (not the inverse of F - see below for that case). F must be non-vanishing, else the derivative doesn't exist at the point that it does become zero (since a division by zero is undefined). The reciprocal of F is,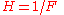
So the derivative in prime notation:
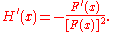
In Leibniz's notation,
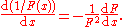
The inverse function rule
This should not be confused with the reciprocal rule (see above): the inverse of a functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
is its inverse with respect to function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, not with respect to the product of functions.
If the function F has an inverse G = F−1, so that G(F(x)) = x and F(G(y)) = y, then in prime notation:
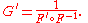
In Leibniz notation, this is written (suggestively) as
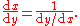
The quotient rule
If F and G are functions, and wherever G is nonzero, then: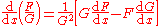
This can be derived from reciprocal rule and the product rule. Conversely (using the constant rule) the reciprocal rule is the special case F(x) = 1.
Logarithmic derivatives
The logarithmic derivativeLogarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
is another way of stating the rule for differentiating the logarithm of a function (using the chain rule):

wherever F is positive (since the logarithm of a negative number is undefined, and requres the complex logarithm
Complex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
for evaluation).
Derivatives of exponential and logarithmic functions
For the exponential function: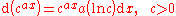
NB: The equation above is true for all c, but the derivative for c < 0 yields a complex number.
A corollary is

For the natural logarithm:
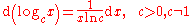
The equation above is also true for all c but yields a complex number.
Further rules:
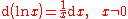
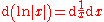

The derivative of the natural logarithm of a generalised function argument F(x) is
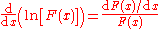
By applying the change-of-base rule, the derivative for the logarithm to a base b is:
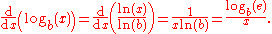
Derivatives of trigonometric functions
 |
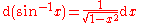 |
 |
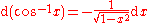 |
 |
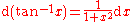 |
 |
|
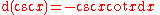 |
|
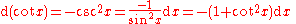 |
 |
Derivatives of hyperbolic functions
 |
 |
 |
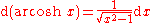 |
 |
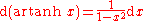 |
 |
 |
 |
|
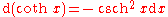 |
 |
Derivatives of special functions
Gamma function Gamma function In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers... 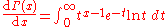 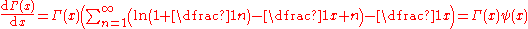 |
Riemann Zeta function  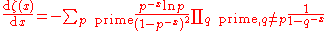 |
Nth Derivatives
The following formulae can be obtained empirically by repeated differentiation and taking notice of patterns; either by hand or computed by a CAS (Computer Algebra System)Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
. Below y is the dependent variable, x is the independent variable, real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
constants are A, B, N, r, real integers are n and j, F(x) is a continuously differentiable function (the nth derivative exists), and i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
 .
.| Function | nth Derivative |
|---|---|
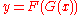 |
where 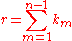 and the set 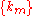 consists of all non-negative integer solutions of the Diophantine equation consists of all non-negative integer solutions of the Diophantine equation 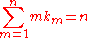 See: Faà di Bruno's formula Faà di Bruno's formula Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula... , Expansions for nearly Gaussian distributions by S. Blinnikov and R. Moessner |
 |
 See: General Leibniz rule |
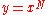 |
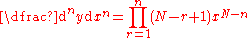 |
 |
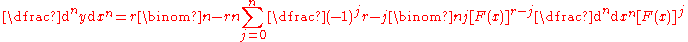 |
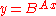 |
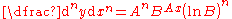 |
For the case of 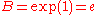 (the exponential function (the exponential functionExponential function In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,... ), the above reduces to: 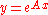 |
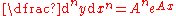 |
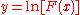 |
 where 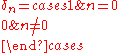 is the Kronecker delta. is the Kronecker delta. |
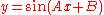 |
 Expanding this by the sine addition formula yields a more clear form to use:  |
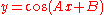 |
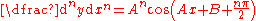 Expanding by the cosine addition formula:  |
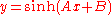 |
 |
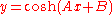 |
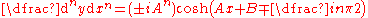 |

