Differentiation in Fréchet spaces
Encyclopedia
In mathematics
, in particular in functional analysis
and nonlinear analysis, it is possible to define the derivative
of a function between two Fréchet space
s. This notion of differentiation is significantly weaker than the derivative in a Banach space
. Nevertheless, it is the weakest notion of differentiation for which many of the familiar theorems from calculus
hold. In particular, the chain rule
is true. With some additional constraints on the Fréchet spaces and functions involved, there is an analog of the inverse function theorem
called the Nash–Moser inverse function theorem, having wide applications in nonlinear analysis and differential geometry.
. Specifically, let X and Y be Fréchet spaces, U ⊂ X be an open set
, and F : U → Y be a function. The directional derivative of F in the direction v ∈ X is defined by
if the limit exists. One says that F is continuously differentiable, or C1 if the limit exists for all h ∈ X and the mapping
is a continuous map.
Higher order derivatives are defined inductively via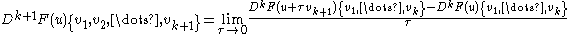
.
A function is said to be Ck if DF : U x X x Xx ... x X → Y is continuous. It is C∞, or smooth if it is Ck for every k.
The proofs of many of these properties rely fundamentally on the fact that it is possible to define the Riemann integral
of continuous curves in a Fréchet space.
. Furthermore, the linearity of the derivative implies that there is an analog of the tangent bundle
for Fréchet manifolds.
. On tame spaces, it is possible to define a preferred class of mappings, known as tame maps. On the category of tame spaces under tame maps, the underlying topology is strong enough to support a fully fledged theory of differential topology
. Within this context, many more techniques from calculus hold. In particular, there are versions of the inverse and implicit function theorems.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and nonlinear analysis, it is possible to define the derivative
Derivative (generalizations)
The derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, and geometry.- Derivatives in analysis :...
of a function between two Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s. This notion of differentiation is significantly weaker than the derivative in a Banach space
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
. Nevertheless, it is the weakest notion of differentiation for which many of the familiar theorems from calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
hold. In particular, the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
is true. With some additional constraints on the Fréchet spaces and functions involved, there is an analog of the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
called the Nash–Moser inverse function theorem, having wide applications in nonlinear analysis and differential geometry.
Mathematical details
Formally, the definition of differentiation is identical to the Gâteaux derivativeGâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
. Specifically, let X and Y be Fréchet spaces, U ⊂ X be an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, and F : U → Y be a function. The directional derivative of F in the direction v ∈ X is defined by
if the limit exists. One says that F is continuously differentiable, or C1 if the limit exists for all h ∈ X and the mapping
- DF:U x X → Y
is a continuous map.
Higher order derivatives are defined inductively via
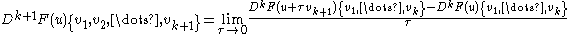.A function is said to be Ck if DF : U x X x Xx ... x X → Y is continuous. It is C∞, or smooth if it is Ck for every k.
Properties
Let X, Y, and Z be Fréchet spaces. Suppose that U is an open subset of X, V is an open subset of Y, and F : U → V, G : V → Z are a pair of C1 functions. Then the following properties hold:- (Fundamental theorem of calculus.)
-
- If the line segment from a to b lies entirely within U, then
.
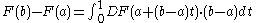- (The chain rule.)
-
- D(G o F)(u)x = DG(F(u))DF(u)x for all u ε U and x ε X.
- (Linearity.)
-
- DF(u)x is linear in x. More generally, if F is Ck, then DF(u){x1,...,xk} is multilinear in the x's.
- (Taylor's theorem with remainder.)
-
- Suppose that the line segment between u ε U and u+h lies entirely within u. If F is Ck then
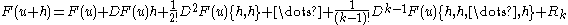
- where the remainder term is given by
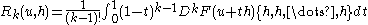
- (Commutativity of directional derivatives.) If F is Ck, then
-
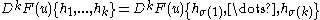for every permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
σ of {1,2,...,k}.
The proofs of many of these properties rely fundamentally on the fact that it is possible to define the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
of continuous curves in a Fréchet space.
Consequences in differential geometry
The existence of a chain rule allows for the definition of a manifold modeled on a Frèchet space: a Fréchet manifoldFréchet manifold
In mathematics, in particular in nonlinear analysis, a Fréchet manifold is a topological space modeled on a Fréchet space in much the same way as a manifold is modeled on a Euclidean space....
. Furthermore, the linearity of the derivative implies that there is an analog of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
for Fréchet manifolds.
Tame Fréchet spaces
Frequently the Fréchet spaces that arise in practical applications of the derivative enjoy an additional property: they are tame. Roughly speaking, a tame Fréchet space is one which is almost a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. On tame spaces, it is possible to define a preferred class of mappings, known as tame maps. On the category of tame spaces under tame maps, the underlying topology is strong enough to support a fully fledged theory of differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
. Within this context, many more techniques from calculus hold. In particular, there are versions of the inverse and implicit function theorems.