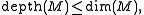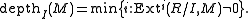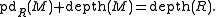Depth (ring theory)
Encyclopedia
In commutative
and homological
algebra, depth is an important invariant of ring
s and modules
. Although depth can be defined more generally, the most common case considered is the case of modules over a commutative Noetherian
local ring
. In this case, the depth of a module is related with its projective dimension by the Auslander–Buchsbaum formula
. A more elementary property of depth is the inequality
where dim M denotes the Krull dimension
of the module M. Depth is used to define classes of rings and modules with good properties, for example, Cohen-Macaulay ring
s and modules, for which the equality holds.
By definition, the depth of a ring R is its depth as a module over itself.
By a theorem of David Rees
, the depth can also be characterized using the notion of a regular sequence
.
with the maximal ideal
and M is a finitely generated R-module. Then all maximal regular sequence
s x1,..., xn for M, where each xi belongs to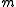
, have the same length n equal to the 
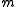-depth of M.
Suppose that R is a commutative Noetherian local ring
with the maximal ideal
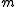and M is a finitely generated R-module. If the projective dimension of M is finite, then the Auslander–Buchsbaum formula states
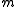is an associated prime, or, equivalently, when there is a nonzero element x of R such that 
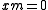(that is, x annihilates 
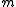). This means, essentially, that the closed point is an embedded component.
For example, the ring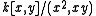
(where k is a field), which represents a line (
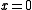) with an embedded double point at the origin, has depth zero at the origin, but dimension one: this gives an example of a ring which is not Cohen–Macaulay.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and homological
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
algebra, depth is an important invariant of ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s and modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. Although depth can be defined more generally, the most common case considered is the case of modules over a commutative Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
. In this case, the depth of a module is related with its projective dimension by the Auslander–Buchsbaum formula
Auslander–Buchsbaum formula
In commutative algebra, the Auslander–Buchsbaum formula, introduced by , states that if R is a commutative Noetherian local ring and M is a finitely generated R-module of finite projective dimension, then...
. A more elementary property of depth is the inequality
where dim M denotes the Krull dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of the module M. Depth is used to define classes of rings and modules with good properties, for example, Cohen-Macaulay ring
Cohen-Macaulay ring
In mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality....
s and modules, for which the equality holds.
Definition
Let R be a commutative Noetherian ring, I an ideal of R and M a finite R-module with the property that IM is properly contained in M. Then the I-depth of M, also commonly called the grade of M, is defined as
By definition, the depth of a ring R is its depth as a module over itself.
By a theorem of David Rees
David Rees (mathematician)
David Rees ScD Cantab, FIMA, FRS is an emeritus professor of pure mathematics at the University of Exeter, having been head of the Mathematics / Mathematical Sciences Department at Exeter for many years....
, the depth can also be characterized using the notion of a regular sequence
Regular sequence (algebra)
In commutative algebra, if R is a commutative ring and M an R-module, a nonzero element r in R is called M-regular if r is not a zerodivisor on M, and M/rM is nonzero...
.
Theorem (Rees)
Suppose that R is a commutative Noetherian local ringLocal ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
with the maximal ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
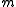and M is a finitely generated R-module. Then all maximal regular sequenceRegular sequence (algebra)
In commutative algebra, if R is a commutative ring and M an R-module, a nonzero element r in R is called M-regular if r is not a zerodivisor on M, and M/rM is nonzero...
s x1,..., xn for M, where each xi belongs to
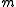, have the same length n equal to the 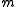-depth of M.Depth and projective dimension
The projective dimension and the depth of a module over a commutative Noetherian local ring are complementary to each other. This is the content of the Auslander–Buchsbaum formula, which is not only of the fundamental theoretical importance, but also provides an effective way to compute the depth of a module.Suppose that R is a commutative Noetherian local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
with the maximal ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
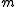and M is a finitely generated R-module. If the projective dimension of M is finite, then the Auslander–Buchsbaum formula states
Depth zero rings
A commutative Noetherian local ring R has depth zero if and only if its maximal ideal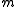 is an associated prime, or, equivalently, when there is a nonzero element x of R such that 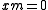(that is, x annihilates 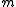). This means, essentially, that the closed point is an embedded component.For example, the ring
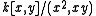(where k is a field), which represents a line (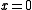) with an embedded double point at the origin, has depth zero at the origin, but dimension one: this gives an example of a ring which is not Cohen–Macaulay.