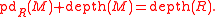Auslander–Buchsbaum formula
Encyclopedia
In commutative algebra
, the Auslander–Buchsbaum formula, introduced by , states that if R is a commutative Noetherian
local ring
and M is a finitely generated R-module of finite projective dimension, then
Here pd stands for the projective dimension of a module, and depth for the depth
of a module.
if, and only if, it has finite global dimension
. In turn this implies that the localization
of a regular local ring is regular.
If A is a local finitely generated R-algebra (over a regular local ring R), then the Auslander–Buchsbaum formula implies that A is Cohen–Macaulay if, and only if, pdRA = codimRA.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the Auslander–Buchsbaum formula, introduced by , states that if R is a commutative Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
and M is a finitely generated R-module of finite projective dimension, then
Here pd stands for the projective dimension of a module, and depth for the depth
Depth (ring theory)
In commutative and homological algebra, depth is an important invariant of rings and modules. Although depth can be defined more generally, the most common case considered is the case of modules over a commutative Noetherian local ring. In this case, the depth of a module is related with its...
of a module.
Applications
The Auslander–Buchsbaum formula implies that a Noetherian local ring is regularRegular local ring
In commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
if, and only if, it has finite global dimension
Global dimension
In ring theory and homological algebra, the global dimension of a ring A denoted gl dim A, is a non-negative integer or infinity which is a homological invariant of the ring. It is defined to be the supremum of the set of projective dimensions of all A-modules...
. In turn this implies that the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of a regular local ring is regular.
If A is a local finitely generated R-algebra (over a regular local ring R), then the Auslander–Buchsbaum formula implies that A is Cohen–Macaulay if, and only if, pdRA = codimRA.