De Donder–Weyl theory
Encyclopedia
The De Donder–Weyl theory is a formalism in the calculus of variations
over spacetime
which treats the space and time coordinates on equal footing. In this framework, a field
is represented as a system that varies both in space and in time.
be spacetime
coordinates, for i=1 to n (with n=4 representing 3+1 dimensions of space and time), and
field variables, for a=1 to m, and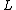 
the Lagrangian density.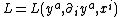
With polymomenta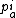
defined as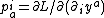
and for De Donder–Weyl Hamiltonian function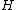
defined as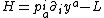
the De Donder–Weyl equations are: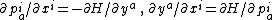
These canonical equations of motion are covariant. The theory is a formulation of a covariant Hamiltonian field theory
and for n=1 it reduces to Hamiltonian mechanics
(see also action principle in the calculus of variations).
and, independently, by Théophile de Donder
. Weyl's made his proposal in 1934, inspired by work of Constantin Carathéodory
which in turn was founded on the work of Vito Volterra
. The work of De Donder in contrast started from the theory of integral invariants
. The De Donder–Weyl theory has thus known in the calculus of variations since the 1930s, and initially found only rare application in physics. It has recently found increased interest in theoretical physics in relation to quantum field theory
.
In 1970, Jedrzej Śniatycki, author of book on Geometric quantization and quantum mechanics, developed an invariant geometrical formulation of jet bundle
s building on the work of De Donder and Weyl. Theoretical physicist Igor V. Kanatchikov showed in 1999 that the De Donder–Weyl covariant Hamiltonian field equations can be formulated in terms of Duffin–Kemmer–Petiau matrices
.
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
over spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
which treats the space and time coordinates on equal footing. In this framework, a field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
is represented as a system that varies both in space and in time.
| De Donder–Weyl equations: |
 |
 |
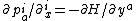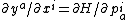De Donder–Weyl formulation of field theory
The De Donder–Weyl theory is based on a change of variables. Let be spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
coordinates, for i=1 to n (with n=4 representing 3+1 dimensions of space and time), and
field variables, for a=1 to m, and 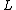the Lagrangian density.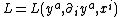With polymomenta
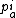defined as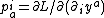and for De Donder–Weyl Hamiltonian function
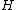defined as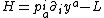the De Donder–Weyl equations are:
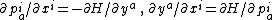
These canonical equations of motion are covariant. The theory is a formulation of a covariant Hamiltonian field theory
Covariant Hamiltonian field theory
Applied to classical field theory, the familiar symplectic Hamiltonian formalism takes the form of instantaneous Hamiltonian formalism on an infinite-dimensional phase space, where canonical coordinates are field functions at some instant of time...
and for n=1 it reduces to Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
(see also action principle in the calculus of variations).
History
The formalism, now known as De Donder–Weyl (DW) theory, was developed by Hermann WeylHermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
and, independently, by Théophile de Donder
Théophile de Donder
Théophile Ernest de Donder was a Belgian mathematician and physicist famous for his 1923 work in developing correlations between the Newtonian concept of chemical affinity and the Gibbsian concept of free energy.-Education:...
. Weyl's made his proposal in 1934, inspired by work of Constantin Carathéodory
Constantin Carathéodory
Constantin Carathéodory was a Greek mathematician. He made significant contributions to the theory of functions of a real variable, the calculus of variations, and measure theory...
which in turn was founded on the work of Vito Volterra
Vito Volterra
Vito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
. The work of De Donder in contrast started from the theory of integral invariants
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
. The De Donder–Weyl theory has thus known in the calculus of variations since the 1930s, and initially found only rare application in physics. It has recently found increased interest in theoretical physics in relation to quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
In 1970, Jedrzej Śniatycki, author of book on Geometric quantization and quantum mechanics, developed an invariant geometrical formulation of jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
s building on the work of De Donder and Weyl. Theoretical physicist Igor V. Kanatchikov showed in 1999 that the De Donder–Weyl covariant Hamiltonian field equations can be formulated in terms of Duffin–Kemmer–Petiau matrices
Duffin–Kemmer–Petiau algebra
In mathematical physics, the Duffin–Kemmer–Petiau algebra , introduced by R.J. Duffin, Nicholas Kemmer and G. Petiau, is the algebra which is generated by the Duffin–Kemmer–Petiau matrices...
.
Further reading
- Cornelius Paufler, Hartmann Römer: De Donder–Weyl equations and multisymplectic geometry, Reports on Mathematical Physics, vol. 49 (2002), no. 2–3, pp. 325–334
- Krzysztof Maurin: The Riemann legacy: Riemannian ideas in mathematics and physics, Part II, Chapter 7.16 Field theories for calculus of variation for multiple integrals, Kluwer Academic Publishers, ISBN 0-7923-4636-X, 1997, p. 482 ff.