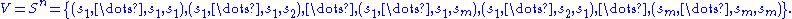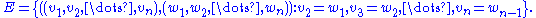
De Bruijn graph
Encyclopedia
In graph theory
, an n-dimensional De Bruijn graph of m symbols is a directed graph
representing overlaps between sequences of symbols. It has mn vertices, consisting of all possible length-n sequences of the given symbols; the same symbol may appear multiple times in a sequence. If we have the set of m symbols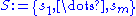
then the set of vertices is:
If one of the vertices can be expressed as another vertex by shifting all its symbols by one place to the left and adding a new symbol at the end of this vertex, then the latter has a directed edge to the former vertex. Thus the set of (directed) edges is
Although De Bruijn graphs are named after Nicolaas Govert de Bruijn
, they were discovered independently by both De Bruijn and I. J. Good
. Much earlier, Flye Sainte-Marie implicitly used their properties.
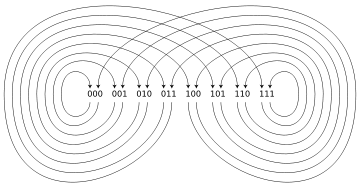
The line graph
construction of the three smallest binary De Bruijn graphs is depicted below. As can be seen in the illustration, each vertex of the n-dimensional De Bruijn graph corresponds to an edge of the (n − 1)-dimensional De Bruijn graph, and each edge in the n-dimensional De Bruijn graph corresponds to a two-edge path in the (n − 1)-dimensional De Bruijn graph.
s, such as the Lorenz attractor
(below, right):
This analogy can be made rigorous: the n-dimensional m-symbol De Bruijn graph is a model of the Bernoulli map
The Bernoulli map (also called the 2x mod 1 map for m = 2) is an ergodic dynamical system, which can be understood to be a single shift
of a m-adic number . The trajectories of this dynamical system correspond to walks in the De Bruijn graph, where the correspondence is given by mapping each real x in the interval [0,1) to the vertex corresponding to the first n digits in the base
-m representation of x. Equivalently, walks in the De Bruijn graph correspond to trajectories in a one-sided subshift of finite type
.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an n-dimensional De Bruijn graph of m symbols is a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
representing overlaps between sequences of symbols. It has mn vertices, consisting of all possible length-n sequences of the given symbols; the same symbol may appear multiple times in a sequence. If we have the set of m symbols
then the set of vertices is:
If one of the vertices can be expressed as another vertex by shifting all its symbols by one place to the left and adding a new symbol at the end of this vertex, then the latter has a directed edge to the former vertex. Thus the set of (directed) edges is
Although De Bruijn graphs are named after Nicolaas Govert de Bruijn
Nicolaas Govert de Bruijn
Nicolaas Govert de Bruijn is a Dutch mathematician, affiliated as professor emeritus with the Eindhoven University of Technology. He received his Ph.D. in 1943 from Vrije Universiteit Amsterdam....
, they were discovered independently by both De Bruijn and I. J. Good
I. J. Good
Irving John Good was a British mathematician who worked as a cryptologist at Bletchley Park with Alan Turing. After World War II, Good continued to work with Turing on the design of computers and Bayesian statistics at the University of Manchester...
. Much earlier, Flye Sainte-Marie implicitly used their properties.
Properties
- If n = 1 then the condition for any two vertices forming an edge holds vacuously, and hence all the vertices are connected forming a total of m2 edges.
- Each vertex has exactly
incoming and m outgoing edges. - Each n-dimensional De Bruijn graph is the line digraphLine graphIn graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
of the (n − 1)-dimensional De Bruijn graph with the same set of symbols . - Each De Bruijn graph is Eulerian and Hamiltonian. The Euler cycles and Hamiltonian cycles of these graphs (equivalent to each other via the line graph construction) are De Bruijn sequenceDe Bruijn sequenceIn combinatorial mathematics, a k-ary De Bruijn sequence B of order n, named after the Dutch mathematician Nicolaas Govert de Bruijn, is a cyclic sequence of a given alphabet A with size k for which every possible subsequence of length n in A appears as a sequence of consecutive characters exactly...
s.
The line graph
Line graph
In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
construction of the three smallest binary De Bruijn graphs is depicted below. As can be seen in the illustration, each vertex of the n-dimensional De Bruijn graph corresponds to an edge of the (n − 1)-dimensional De Bruijn graph, and each edge in the n-dimensional De Bruijn graph corresponds to a two-edge path in the (n − 1)-dimensional De Bruijn graph.
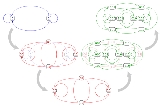
Dynamical systems
Binary De Bruijn graphs can be drawn (below, left) in such a way that they resemble objects from the theory of dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, such as the Lorenz attractor
Lorenz attractor
The Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...
(below, right):
This analogy can be made rigorous: the n-dimensional m-symbol De Bruijn graph is a model of the Bernoulli map
The Bernoulli map (also called the 2x mod 1 map for m = 2) is an ergodic dynamical system, which can be understood to be a single shift
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
of a m-adic number . The trajectories of this dynamical system correspond to walks in the De Bruijn graph, where the correspondence is given by mapping each real x in the interval [0,1) to the vertex corresponding to the first n digits in the base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
-m representation of x. Equivalently, walks in the De Bruijn graph correspond to trajectories in a one-sided subshift of finite type
Subshift of finite type
In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine...
.
Uses
- Some grid networkGrid networkA grid network is a kind of computer network consisting of a number of systems connected in a grid topology.In a regular grid topology, each node in the network is connected with two neighbors along one or more dimensions. If the network is one-dimensional, and the chain of nodes is connected to...
topologies are De Bruijn graphs. - The distributed hash tableDistributed hash tableA distributed hash table is a class of a decentralized distributed system that provides a lookup service similar to a hash table; pairs are stored in a DHT, and any participating node can efficiently retrieve the value associated with a given key...
protocol KoordeKoordeIn peer-to-peer networks, Koorde is a Distributed hash table system based on the Chord DHT and the De Bruijn graph . Inheriting the simplicity of Chord, Koorde meets O hops per node , and O hops per lookup request with O neighbors per node.The Chord concept is based on a wide range of...
uses a De Bruijn graph. - In bioinformaticsBioinformaticsBioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
De Bruijn graphs are used for de novo assembly of (short) read sequences into a genomeGenomeIn modern molecular biology and genetics, the genome is the entirety of an organism's hereditary information. It is encoded either in DNA or, for many types of virus, in RNA. The genome includes both the genes and the non-coding sequences of the DNA/RNA....
.