Koorde
Encyclopedia
In peer-to-peer
networks, Koorde is a Distributed hash table
(DHT) system based on the Chord DHT and the De Bruijn graph
(De Bruijn sequence
). Inheriting the simplicity of Chord, Koorde meets O(log n) hops per node (where n is the number of nodes in the DHT), and O(log n/ log log n) hops per lookup request with O(log n) neighbors per node.
The Chord concept is based on a wide range of identifiers (e.g. 2^160) in a structure of a ring where an identifier can stand for both node and data. Node-successor is responsible for the whole range of IDs between itself and its predecessor.
(De Bruijn sequence
).
In a d-dimensional de Bruijn graph, there are 2d nodes, each of which has a unique d-bit ID. The node with ID i is connected to nodes 2i modulo 2d and 2i+1 modulo 2d. Thanks to this property, the routing algorithm can route to any destination in d hops by successively „shifting in” the bits of the destination ID but only if the dimensions of the distance between modulo 1d and 3d are equal.
Routing a message from node m to node k is accomplished by taking the number m and shifting in the bits of k one at a time until the number has been replaced by k. Each shift corresponds to a routing hop to the next intermediate address; the hop is valid because each node's neighbors are the two possible outcomes of shifting a 0 or 1 onto its own address. Because of the structure of de Bruijn graphs, when the last bit of k has been shifted, the query will be at node k. Node k responds whether key k exists.
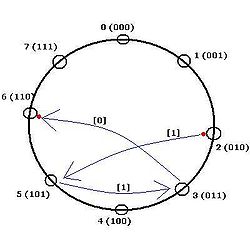For example, when a message needs to be routed from node “2” (which is “010”) to “6” (which is “110”), the steps are following:
Step 1)
Node #2 routes the message to Node #5 (using its connection to 2i+1 mod8), shifts the bits left and puts “1” as the youngest bit (right side).
Step 2)
Node #5 routes the message to Node #3 (using its connection to 2i+1 mod8), shifts the bits left and puts “1” as the youngest bit (right side).
Step 3)
Node #3 routes the message to Node #6 (using its connection to 2i mod8), shifts the bits left and puts “0” as the youngest bit (right side).
The d-dimensional de Bruijn can be generalized to base k, in which case node i is connected to nodes k * i + j modulo kd, 0 ≤ j < k. The diameter is reduced to Θ(logk n). Koorde node i maintains pointers to k consecutive nodes beginning at the predecessor of k * i modulo kd. Each de Bruijn routing step can be emulated with an expected constant number of messages, so routing uses O(logk n) expected hops- For k = Θ(log n), we get Θ(log n) degree and Θ(log n/ log log n) diameter.
Peer-to-peer
Peer-to-peer computing or networking is a distributed application architecture that partitions tasks or workloads among peers. Peers are equally privileged, equipotent participants in the application...
networks, Koorde is a Distributed hash table
Distributed hash table
A distributed hash table is a class of a decentralized distributed system that provides a lookup service similar to a hash table; pairs are stored in a DHT, and any participating node can efficiently retrieve the value associated with a given key...
(DHT) system based on the Chord DHT and the De Bruijn graph
De Bruijn graph
In graph theory, an n-dimensional De Bruijn graph of m symbols is a directed graph representing overlaps between sequences of symbols. It has mn vertices, consisting of all possible length-n sequences of the given symbols; the same symbol may appear multiple times in a sequence...
(De Bruijn sequence
De Bruijn sequence
In combinatorial mathematics, a k-ary De Bruijn sequence B of order n, named after the Dutch mathematician Nicolaas Govert de Bruijn, is a cyclic sequence of a given alphabet A with size k for which every possible subsequence of length n in A appears as a sequence of consecutive characters exactly...
). Inheriting the simplicity of Chord, Koorde meets O(log n) hops per node (where n is the number of nodes in the DHT), and O(log n/ log log n) hops per lookup request with O(log n) neighbors per node.
The Chord concept is based on a wide range of identifiers (e.g. 2^160) in a structure of a ring where an identifier can stand for both node and data. Node-successor is responsible for the whole range of IDs between itself and its predecessor.
De Bruijn's graphs
Koorde is based on Chord but also on De Bruijn graphDe Bruijn graph
In graph theory, an n-dimensional De Bruijn graph of m symbols is a directed graph representing overlaps between sequences of symbols. It has mn vertices, consisting of all possible length-n sequences of the given symbols; the same symbol may appear multiple times in a sequence...
(De Bruijn sequence
De Bruijn sequence
In combinatorial mathematics, a k-ary De Bruijn sequence B of order n, named after the Dutch mathematician Nicolaas Govert de Bruijn, is a cyclic sequence of a given alphabet A with size k for which every possible subsequence of length n in A appears as a sequence of consecutive characters exactly...
).
In a d-dimensional de Bruijn graph, there are 2d nodes, each of which has a unique d-bit ID. The node with ID i is connected to nodes 2i modulo 2d and 2i+1 modulo 2d. Thanks to this property, the routing algorithm can route to any destination in d hops by successively „shifting in” the bits of the destination ID but only if the dimensions of the distance between modulo 1d and 3d are equal.
Routing a message from node m to node k is accomplished by taking the number m and shifting in the bits of k one at a time until the number has been replaced by k. Each shift corresponds to a routing hop to the next intermediate address; the hop is valid because each node's neighbors are the two possible outcomes of shifting a 0 or 1 onto its own address. Because of the structure of de Bruijn graphs, when the last bit of k has been shifted, the query will be at node k. Node k responds whether key k exists.
Routing example
Step 1)
Node #2 routes the message to Node #5 (using its connection to 2i+1 mod8), shifts the bits left and puts “1” as the youngest bit (right side).
Step 2)
Node #5 routes the message to Node #3 (using its connection to 2i+1 mod8), shifts the bits left and puts “1” as the youngest bit (right side).
Step 3)
Node #3 routes the message to Node #6 (using its connection to 2i mod8), shifts the bits left and puts “0” as the youngest bit (right side).
Non-constant degree Koorde