
Cut locus (Riemannian manifold)
Encyclopedia
In Riemannian geometry
, the cut locus of a point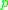 in a manifold
in a manifold
is roughly the set of all other points for which there are multiple minimizing geodesics
connecting them from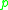 , but it may contain additional points where the minimizing geodesic is unique, under certain circumstances. The distance function from p is a smooth
, but it may contain additional points where the minimizing geodesic is unique, under certain circumstances. The distance function from p is a smooth
function except at the point p itself and the cut locus.
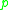 in a complete
in a complete
Riemannian manifold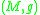 , and consider the tangent space
, and consider the tangent space
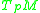 . It is a standard result that for sufficiently small
. It is a standard result that for sufficiently small  in
in 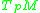 , the curve defined by the Riemannian exponential map,
, the curve defined by the Riemannian exponential map, 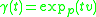 for
for  belonging to the interval
belonging to the interval 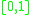 is a minimizing geodesic
is a minimizing geodesic
, and is the unique minimizing geodesic connecting the two endpoints. Here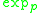 denotes the exponential map
denotes the exponential map
from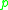 . The cut locus of
. The cut locus of 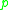 in the tangent space is defined to be the set of all vectors
in the tangent space is defined to be the set of all vectors  in
in 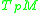 such that
such that 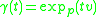 is a minimizing geodesic for
is a minimizing geodesic for 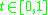 but fails to be minimizing for
but fails to be minimizing for 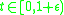 for each
for each  . The cut locus of
. The cut locus of 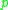 in
in 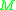 is defined to be image of the
is defined to be image of the
cut locus of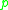 in the tangent space under the exponential map at
in the tangent space under the exponential map at 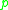 . Thus, we may interpret the cut locus of
. Thus, we may interpret the cut locus of 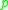 in
in 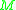 as the points in the manifold where the geodesics starting at
as the points in the manifold where the geodesics starting at 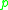 stop being minimizing.
stop being minimizing.
The least distance from p to the cut locus is the injectivity radius at p. On the open ball of this radius, the exponential map at p is a diffeomorphism from the tangent space to the manifold, and this is the largest such radius. The global injectivity radius is defined to be the infimum of the injectivity radius at p, over all points of the manifold.
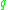 is in the cut locus of
is in the cut locus of 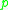 in
in 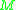 . A standard result is that either (1) there is more than one minimizing
. A standard result is that either (1) there is more than one minimizing
geodesic joining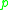 to
to 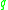 , or (2)
, or (2) 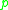 and
and 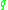 are conjugate along some geodesic
are conjugate along some geodesic
which joins them. It is possible for both (1) and (2) to hold.
, the cut locus of a point consists of the single point opposite of it (i.e., the antipodal point
). On
an infinitely long cylinder
, the cut locus of a point consists of the line opposite the point.
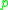 is smooth, except on the cut locus of
is smooth, except on the cut locus of 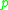 . In particular, it makes sense to take the gradient
. In particular, it makes sense to take the gradient
and Hessian
of the distance function away from the cut locus. This idea is used in the local Laplacian comparison theorem and the local Hessian comparison theorem. These are used in the proof of the local version of the Toponogov theorem, and many other important theorems in Riemannian geometry.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the cut locus of a point
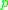 in a manifold
in a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is roughly the set of all other points for which there are multiple minimizing geodesics
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
connecting them from
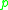 , but it may contain additional points where the minimizing geodesic is unique, under certain circumstances. The distance function from p is a smooth
, but it may contain additional points where the minimizing geodesic is unique, under certain circumstances. The distance function from p is a smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
function except at the point p itself and the cut locus.
Definition
Fix a point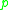 in a complete
in a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
Riemannian manifold
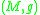 , and consider the tangent space
, and consider the tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
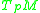 . It is a standard result that for sufficiently small
. It is a standard result that for sufficiently small  in
in 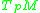 , the curve defined by the Riemannian exponential map,
, the curve defined by the Riemannian exponential map, 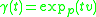 for
for  belonging to the interval
belonging to the interval 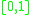 is a minimizing geodesic
is a minimizing geodesicGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
, and is the unique minimizing geodesic connecting the two endpoints. Here
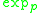 denotes the exponential map
denotes the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
from
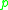 . The cut locus of
. The cut locus of 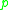 in the tangent space is defined to be the set of all vectors
in the tangent space is defined to be the set of all vectors  in
in 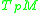 such that
such that 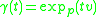 is a minimizing geodesic for
is a minimizing geodesic for 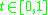 but fails to be minimizing for
but fails to be minimizing for 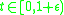 for each
for each  . The cut locus of
. The cut locus of 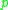 in
in 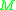 is defined to be image of the
is defined to be image of thecut locus of
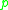 in the tangent space under the exponential map at
in the tangent space under the exponential map at 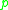 . Thus, we may interpret the cut locus of
. Thus, we may interpret the cut locus of 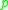 in
in 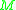 as the points in the manifold where the geodesics starting at
as the points in the manifold where the geodesics starting at 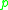 stop being minimizing.
stop being minimizing.The least distance from p to the cut locus is the injectivity radius at p. On the open ball of this radius, the exponential map at p is a diffeomorphism from the tangent space to the manifold, and this is the largest such radius. The global injectivity radius is defined to be the infimum of the injectivity radius at p, over all points of the manifold.
Characterization
Suppose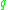 is in the cut locus of
is in the cut locus of 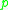 in
in 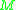 . A standard result is that either (1) there is more than one minimizing
. A standard result is that either (1) there is more than one minimizinggeodesic joining
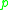 to
to 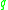 , or (2)
, or (2) 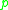 and
and 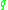 are conjugate along some geodesic
are conjugate along some geodesicwhich joins them. It is possible for both (1) and (2) to hold.
Examples
On the standard round n-sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, the cut locus of a point consists of the single point opposite of it (i.e., the antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
). On
an infinitely long cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
, the cut locus of a point consists of the line opposite the point.
Applications
The significance of the cut locus is that the distance function from a point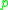 is smooth, except on the cut locus of
is smooth, except on the cut locus of 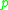 . In particular, it makes sense to take the gradient
. In particular, it makes sense to take the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and Hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of the distance function away from the cut locus. This idea is used in the local Laplacian comparison theorem and the local Hessian comparison theorem. These are used in the proof of the local version of the Toponogov theorem, and many other important theorems in Riemannian geometry.

