Critical mass - AbsoluteAstronomy.com

A critical mass is the smallest amount of fissile

Fissile

In nuclear engineering, a fissile material is one that is capable of sustaining a chain reaction of nuclear fission. By definition, fissile materials can sustain a chain reaction with neutrons of any energy. The predominant neutron energy may be typified by either slow neutrons or fast neutrons...

material needed for a sustained nuclear chain reaction

Nuclear chain reaction

A nuclear chain reaction occurs when one nuclear reaction causes an average of one or more nuclear reactions, thus leading to a self-propagating number of these reactions. The specific nuclear reaction may be the fission of heavy isotopes or the fusion of light isotopes...

. The critical mass of a fissionable material depends upon its nuclear

Atomic nucleus

The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...

properties (e.g. the nuclear fission

Nuclear fission

In nuclear physics and nuclear chemistry, nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts , often producing free neutrons and photons , and releasing a tremendous amount of energy...

cross-section

Cross section (physics)

A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....

), its density

Density

The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...

, its shape

Shape

The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...

, its enrichment

Isotope separation

Isotope separation is the process of concentrating specific isotopes of a chemical element by removing other isotopes, for example separating natural uranium into enriched uranium and depleted uranium. This is a crucial process in the manufacture of uranium fuel for nuclear power stations, and is...

, its purity, its temperature

Temperature

Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...

and its surroundings.

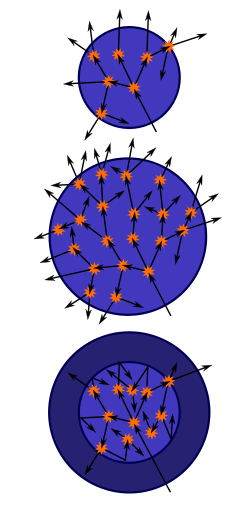
Explanation of criticality

When a nuclear chain reaction in a mass of fissile material is self-sustaining, the mass is said to be in a critical state in which there is no increase or decrease in power, temperature or neutron

Neutron

The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...

population.

A numerical measure of a critical mass is dependent on the effective neutron multiplication factor , the average number of neutrons released per fission event that go on to cause another fission event rather than being absorbed or leaving the material. When

, the mass is critical, and the chain reaction is barely self-sustaining.

A subcritical mass is a mass of fissile material that does not have the ability to sustain a fission chain reaction. A population of neutrons introduced to a subcritical assembly will exponentially decrease. In this case,

. A steady rate of spontaneous fissions causes a proportionally steady level of neutron activity. The constant of proportionality increases as increases.

A supercritical mass is one where there is an increasing rate of fission. The material may settle into equilibrium (i.e. become critical again) at an elevated temperature/power level or destroy itself, by which equilibrium is reached. In the case of supercriticality,

Changing the point of criticality

The point and therefore the mass where criticality occurs may be changed by modifying certain attributes such as fuel, shape, temperature, density and the installation of a neutron-reflective substance. These attributes have complex interactions and interdependencies. This section explains only the simplest ideal cases.

Varying the amount of fuel

It is possible for a fuel assembly to be critical at near zero power. If the perfect quantity of fuel were added to a slightly subcritical mass to create an "exactly critical mass", fission would be self-sustaining for one neutron generation (fuel consumption makes the assembly subcritical).

If the perfect quantity of fuel were added to a slightly subcritical mass, to create a barely supercritical mass, the temperature of the assembly would increase to an initial maximum (for example: 1 K

Kelvin

The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...

above the ambient temperature) and then decrease back to room temperature after a period of time, because fuel consumed during fission brings the assembly back to subcriticality once again.

Changing the shape

A mass may be exactly critical without being a perfect homogeneous sphere. More closely refining the shape toward a perfect sphere will make the mass supercritical. Conversely changing the shape to a less perfect sphere will decrease its reactivity and make it subcritical.

Changing the temperature

A mass may be exactly critical at a particular temperature. Fission and absorption cross-sections increase as the relative neutron velocity decreases. As fuel temperature increases, neutrons of a given energy appear faster and thus fission/absorption is less likely. This is not unrelated to doppler broadening of the U238 resonances but is common to all fuels/absorbers/configurations. Neglecting the very important resonances, the total neutron cross section of every material exhibits an inverse relationship with relative neutron velocity. Hot fuel is always less reactive than cold fuel (over/under moderation in LWR is a different topic). Thermal expansion associated with temperature increase also contributes a negative coefficient of reactivity since fuel atoms are moving farther apart. A mass that is exactly critical at room temperature would be sub-critical in an environment anywhere above room temperature due to thermal expansion alone.

Varying the density of the mass

The higher the density, the lower the critical mass. The density of a material at a constant temperature can be changed by varying the pressure or tension or by changing crystal structure (see Allotropes of plutonium

Allotropes of plutonium

Even at ambient pressure, plutonium occurs in a variety of allotropes. These allotropes differ widely in crystal structure and density; the α and δ allotropes differ in density by more than 25% at constant pressure....

). An ideal mass will become subcritical if allowed to expand or conversely the same mass will become supercritical if compressed. Changing the temperature may also change the density; however, the effect on critical mass is then complicated by temperature effects (See Changing the temperature) and by whether the material expands or contracts with increased temperature. Assuming the material expands with temperature (enriched Uranium 235 at room temperature for example), at an exactly critical state, it will become subcritical if warmed to lower density or become supercritical if cooled to higher density. Such a material is said to have a negative temperature coefficient of reactivity to indicate that its reactivity decreases when its temperature increases. Using such a material as fuel means fission decreases as the fuel temperature increases.

Use of a neutron reflector

Surrounding a spherical critical mass with a neutron reflector further reduces the mass needed for criticality. A common material for a neutron reflector is beryllium

Beryllium

Beryllium is the chemical element with the symbol Be and atomic number 4. It is a divalent element which occurs naturally only in combination with other elements in minerals. Notable gemstones which contain beryllium include beryl and chrysoberyl...

metal. This reduces the number of neutrons which escape the fissile material, resulting in increased reactivity.

Use of a tamper

In a bomb, a dense shell of material surrounding the fissile core will contain, via inertia, the expanding fissioning material.
This increases the efficiency. Because a bomb relies on fast neutrons (not ones moderated by reflection with light elements, as in a reactor) the tamper in a bomb is not functioning as a neutron reflector. Also, if the tamper is (e.g. depleted) uranium, it can fission due to the high energy neutrons generated by the primary explosion. This can greatly increase yield, especially if even more neutrons are generated by fusing hydrogen isotopes, in a so-called boosted configuration.

Critical mass of a bare sphere

The shape with minimal critical mass and the smallest physical dimensions is a sphere.
Bare-sphere critical masses at normal density of some actinides are listed in the following table.

Nuclide	Critical Mass (kg)	Diameter (cm)
uranium-233 Uranium-233 Uranium-233 is a fissile isotope of uranium, bred from Thorium as part of the thorium fuel cycle. It has been used in a few nuclear reactors and has been proposed for much wider use as a nuclear fuel. It has a half-life of 160,000 years....	15	11
uranium-235 Uranium-235 - References :* .* DOE Fundamentals handbook: Nuclear Physics and Reactor theory , .* A piece of U-235 the size of a grain of rice can produce energy equal to that contained in three tons of coal or fourteen barrels of oil. -External links:* * * one of the earliest articles on U-235 for the...	52	17
neptunium-236	7	8.7
neptunium-237	60	18
plutonium-238 Plutonium-238 -External links:**...	9.04–10.07	9.5-9.9
plutonium-239 Plutonium-239 Plutonium-239 is an isotope of plutonium. Plutonium-239 is the primary fissile isotope used for the production of nuclear weapons, although uranium-235 has also been used and is currently the secondary isotope. Plutonium-239 is also one of the three main isotopes demonstrated usable as fuel in...	10	9.9
plutonium-240 Plutonium-240 Plutonium-240 is an isotope of the metal plutonium formed when plutonium-239 captures a neutron. About 62% to 73% of the time when Pu-239 captures a neutron it undergoes fission; the rest of the time it forms Pu-240. The longer a nuclear fuel element remains in a nuclear reactor the greater the...	40	15
plutonium-241 Plutonium-241 Plutonium-241 is an isotope of plutonium formed when plutonium-240 captures a neutron. Like Pu-239 but unlike 240Pu, 241Pu is fissile, with a neutron absorption cross section about 1/3 greater than 239Pu, and a similar probability of fissioning on neutron absorption, around 73%. In the non-fission...	12	10.5
plutonium-242 Plutonium-242 Pu-242 is one of the isotopes of plutonium, the second longest-lived, with a half-life of 373,300 years.242Pu's halflife is about 15 times as long as Pu-239's halflife; therefore it is 1/15 as radioactive and not one of the larger contributors to nuclear waste radioactivity.242Pu's gamma ray...	75–100	19-21
americium-241	55–77	20-23
americium-242	9–14	11-13
americium-243	180–280	30-35
curium Curium Curium is a synthetic chemical element with the symbol Cm and atomic number 96. This radioactive transuranic element of the actinide series was named after Marie Skłodowska-Curie and her husband Pierre Curie. Curium was first intentionally produced and identified in summer 1944 by the group of... -243	7.34–10	10-11
curium Curium Curium is a synthetic chemical element with the symbol Cm and atomic number 96. This radioactive transuranic element of the actinide series was named after Marie Skłodowska-Curie and her husband Pierre Curie. Curium was first intentionally produced and identified in summer 1944 by the group of... -244	(13.5)–30	(12.4)–16
curium Curium Curium is a synthetic chemical element with the symbol Cm and atomic number 96. This radioactive transuranic element of the actinide series was named after Marie Skłodowska-Curie and her husband Pierre Curie. Curium was first intentionally produced and identified in summer 1944 by the group of... -245	9.41–12.3	11-12
curium Curium Curium is a synthetic chemical element with the symbol Cm and atomic number 96. This radioactive transuranic element of the actinide series was named after Marie Skłodowska-Curie and her husband Pierre Curie. Curium was first intentionally produced and identified in summer 1944 by the group of... -246	39–70.1	18-21
curium Curium Curium is a synthetic chemical element with the symbol Cm and atomic number 96. This radioactive transuranic element of the actinide series was named after Marie Skłodowska-Curie and her husband Pierre Curie. Curium was first intentionally produced and identified in summer 1944 by the group of... -247	6.94–7.06	9.9
californium Californium Californium is a radioactive metallic chemical element with the symbol Cf and atomic number 98. The element was first made in the laboratory in 1950 by bombarding curium with alpha particles at the University of California, Berkeley. It is the ninth member of the actinide series and was the... -249	6	9
californium Californium Californium is a radioactive metallic chemical element with the symbol Cf and atomic number 98. The element was first made in the laboratory in 1950 by bombarding curium with alpha particles at the University of California, Berkeley. It is the ninth member of the actinide series and was the... -251	5	8.5
californium Californium Californium is a radioactive metallic chemical element with the symbol Cf and atomic number 98. The element was first made in the laboratory in 1950 by bombarding curium with alpha particles at the University of California, Berkeley. It is the ninth member of the actinide series and was the... -252	2.73	6.9

The critical mass for lower-grade uranium depends strongly on the grade: with 20% U-235 it is over 400 kg; with 15% U-235, it is well over 600 kg.

The critical mass is inversely proportional to the square of the density. If the density is 1% more and the mass 2% less, then the volume is 3% less and the diameter 1% less. The probability for a neutron per cm travelled to hit a nucleus is proportional to the density. It follows that 1% greater density means that the distance travelled before leaving the system is 1% less. This is something that must be taken into consideration when attempting more precise estimates of critical masses of plutonium isotopes than the approximate values given above, because plutonium metal has a large number of different crystal phases which can have widely varying densities.

Note that not all neutrons contribute to the chain reaction. Some escape and others undergo radiative capture

Neutron capture

Neutron capture is a kind of nuclear reaction in which an atomic nucleus collides with one or more neutrons and they merge to form a heavier nucleus. Since neutrons have no electric charge they can enter a nucleus more easily than positively charged protons, which are repelled...

.

Let q denote the probability that a given neutron induces fission in a nucleus. Let us consider only prompt neutron

Prompt neutron

In nuclear engineering, a prompt neutron is a neutron immediately emitted by a nuclear fission event, as opposed to a delayed neutron decay which can occur within the same context, emitted by one of the fission products anytime from a few milliseconds to a few minutes later.-Principle:Using U-235...

s, and let ν denote the number of prompt neutrons generated in a nuclear fission. For example, ν ≈ 2.5 for uranium-235. Then, criticality occurs when ν·q = 1. The dependence of this upon geometry, mass, and density appears through the factor q.

Given a total interaction cross section

Cross section (physics)

σ (typically measured in barns

Barn (unit)

A barn is a unit of area. Originally used in nuclear physics for expressing the cross sectional area of nuclei and nuclear reactions, today it is used in all fields of high energy physics to express the cross sections of any scattering process, and is best understood as a measure of the...

), the mean free path

Mean free path

In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...

of a prompt neutron is

where n is the nuclear number density. Most interactions are scattering events, so that a given neutron obeys a random walk

Random walk

A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...

until it either escapes from the medium or causes a fission reaction. So long as other loss mechanisms are not significant, then, the radius of a spherical critical mass is rather roughly given by the product of the mean free path

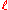and the square root of one plus the number of scattering events per fission event (call this s), since the net distance travelled in a random walk is proportional to the square root of the number of steps:

Note again, however, that this is only a rough estimate.

In terms of the total mass M, the nuclear mass m, the density ρ, and a fudge factor f which takes into account geometrical and other effects, criticality corresponds to

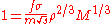
which clearly recovers the aforementioned result that critical mass depends inversely on the square of the density.

Alternatively, one may restate this more succinctly in terms of the areal density of mass, Σ:

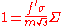
where the factor f has been rewritten as

to account for the fact that the two values may differ depending upon geometrical effects and how one defines Σ. For example, for a bare solid sphere of Pu-239 criticality is at 320 kg/m², regardless of density, and for U-235 at 550 kg/m².
In any case, criticality then depends upon a typical neutron "seeing" an amount of nuclei around it such that the areal density of nuclei exceeds a certain threshold.

This is applied in implosion-type nuclear weapons where a spherical mass of fissile material that is substantially less than a critical mass is made supercritical by very rapidly increasing ρ (and thus Σ as well) (see below). Indeed, sophisticated nuclear weapons programs can make a functional device from less material than more primitive weapons programs require.

Aside from the math, there is a simple physical analog that helps explain this result. Consider diesel fumes belched from an exhaust pipe. Initially the fumes appear black, then gradually you are able to see through them without any trouble. This is not because the total scattering cross section of all the soot particles has changed, but because the soot has dispersed. If we consider a transparent cube of length

on a side, filled with soot, then the optical depth

Optical depth

Optical depth, or optical thickness, is a measure of transparency. Optical depth is defined by the negative logarithm of the fraction of radiation that is not scattered or absorbed on a path...

of this medium is inversely proportional to the square of

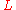, and therefore proportional to the areal density of soot particles: we can make it easier to see through the imaginary cube just by making the cube larger.

Several uncertainties contribute to the determination of a precise value for critical masses, including (1) detailed knowledge of cross sections, (2) calculation of geometric effects. This latter problem provided significant motivation for the development of the Monte Carlo method

Monte Carlo method

Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...

in computational physics by Nicholas Metropolis

Nicholas Metropolis

Nicholas Constantine Metropolis was a Greek American physicist.-Work:Metropolis received his B.Sc. and Ph.D. degrees in physics at the University of Chicago...

and Stanislaw Ulam. In fact, even for a homogeneous solid sphere, the exact calculation is by no means trivial. Finally note that the calculation can also be performed by assuming a continuum approximation for the neutron transport. This reduces it to a diffusion problem. However, as the typical linear dimensions are not significantly larger than the mean free path, such an approximation is only marginally applicable.

Finally, note that for some idealized geometries, the critical mass might formally be infinite, and other parameters are used to describe criticality. For example, consider an infinite sheet of fissionable material. For any finite thickness, this corresponds to an infinite mass. However, criticality is only achieved once the thickness of this slab exceeds a critical value.

Criticality in nuclear weapon design

Until detonation is desired, a nuclear weapon

Nuclear weapon

A nuclear weapon is an explosive device that derives its destructive force from nuclear reactions, either fission or a combination of fission and fusion. Both reactions release vast quantities of energy from relatively small amounts of matter. The first fission bomb test released the same amount...

must be kept subcritical. In the case of a uranium bomb, this can be achieved by keeping the fuel in a number of separate pieces, each below the critical size

Critical size

The critical size is the minimum size of a nuclear reactor core or nuclear weapon that can be made critical for a specific geometrical arrangement and material composition. The critical size must at least include enough fissionable material to reach critical mass...

either because they are too small or unfavorably shaped. To produce detonation, the uranium is brought together rapidly. In Little Boy

Little Boy

"Little Boy" was the codename of the atomic bomb dropped on Hiroshima on August 6, 1945 by the Boeing B-29 Superfortress Enola Gay, piloted by Colonel Paul Tibbets of the 393rd Bombardment Squadron, Heavy, of the United States Army Air Forces. It was the first atomic bomb to be used as a weapon...

, this was achieved by firing a piece of uranium (a 'doughnut'), down a gun barrel

Gun barrel

A gun barrel is the tube, usually metal, through which a controlled explosion or rapid expansion of gases are released in order to propel a projectile out of the end at a high velocity....

onto another piece, (a 'spike'), a design referred to as a gun-type fission weapon
Gun-type fission weapon
Gun-type fission weapons are fission-based nuclear weapons whose design assembles their fissile material into a supercritical mass by the use of the "gun" method: shooting one piece of sub-critical material into another...

.

A theoretical 100% pure Pu-239 weapon could also be constructed as a gun-type weapon, like the Manhattan Project's proposed Thin Man design. In reality, this is impractical because even "weapons grade" Pu-239 is contaminated with a small amount of Pu-240, which has a strong propensity toward spontaneous fission. Because of this, a reasonably-sized gun-type weapon would suffer nuclear reaction before the masses of plutonium would be in a position for a full-fledged explosion to occur.

Instead, the plutonium is present as a subcritical sphere (or other shape), which may or may not be hollow. Detonation is produced by exploding a shaped charge

Shaped charge

A shaped charge is an explosive charge shaped to focus the effect of the explosive's energy. Various types are used to cut and form metal, to initiate nuclear weapons, to penetrate armor, and in the oil and gas industry...

surrounding the sphere, increasing the density (and collapsing the cavity, if present) to produce a prompt critical

Prompt critical

In nuclear engineering, an assembly is prompt critical if for each nuclear fission event, one or more of the immediate or prompt neutrons released causes an additional fission event. This causes a rapid, exponential increase in the number of fission events...

configuration. This is known as an implosion type weapon.

Explanation of criticality

Changing the point of criticality

Critical mass of a bare sphere

Criticality in nuclear weapon design

See also