
Correlate summation analysis
Encyclopedia
Correlate summation analysis is a data mining
method. It is designed to find the variables
that are most covariant
with all of the other variables being studied, relative to clustering
. Aggregate correlate summation is the product of the totaled negative logarithm
of the p-value
s for all of the correlation
s to a given variable and its (normalized) standard deviation
-to-mean
quotient. Discrete correlate summation is the product of the totaled absolute value of the logarithm of the p-value ratios between two groups' correlations to a given variable and its absolute value of the logarithm of the group mean ratios.
http://sites.google.com/site/correlatesummationtemplate/Home/correlate-summation-template/correlate.zip?attredirects=0
The paper describing the method is embedded in the spreadsheet.
(m by m) was constructed for m variables for each group. Each column represents all of the correlations (r) between a given variable and each of the other variables. For variables with either heterogeneous or homogeneous numbers of data points (n), the n for each individual correlation was calculated by assigning each data point with a value of one and taking the sum of the products for each pair in that correlation.
The correlations were tested for linearity using Student's t-distribution to evaluate:
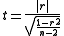
for (n − 2) degrees of freedom, returning two tails .
The correlation matrices were thus transformed into linear probability matrices. For the two groups, the absolute value of the logarithm of the ratio of each comparison’s p-value gives a log correlation ratio that is larger as the ratio approaches zero or infinity. Each column was totaled to form the discrete correlate summation array. As in the log correlation ratio (logcr), the log mean ratio (logmr) for the two groups’ means was acquired for each variable. The correlate summation was then multiplied by the log mean ratio, to yield the discrete mean-correlate summation (DCΣx) .
will have a larger normalized standard deviation (nSD) than will data with a normal distribution. The nSD array multiplied by the ACΣ array yielded the aggregate mean-correlate summation (ACΣx) .
(control
) relationship may be evident. Generally in the face of data that defies linear regression
, data patterns indicate power relationship of the general type:
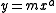
Type 1: a < 0 is a hyperbolic
function
Type 2: a = 0 is a horizontal line
Type 3: 0 < a < 1 is a root
function
Type 4: a = 1 is actually a linear function
Type 5: a > 1 is a power function
(In all five cases a log-log plot yields a linear curve.)
On a positive sigmoidal/logistic curve, the initial, intermediate and late portions resemble power, linear and root functions, respectively. Also, the late portion of a negative control function is reminiscent of a hyperbolic curve.
In an analysis of variable correlation, the sigmoidal relationship of the entire (unsampled in some cases) data range should be considered. This type of analysis is accomplished by regression with either a logistic curve or simple linear regression
with further investigation of the Type 1, 3 and 5 power relationships .
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
method. It is designed to find the variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
that are most covariant
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
with all of the other variables being studied, relative to clustering
Data clustering
Cluster analysis or clustering is the task of assigning a set of objects into groups so that the objects in the same cluster are more similar to each other than to those in other clusters....
. Aggregate correlate summation is the product of the totaled negative logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
s for all of the correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
s to a given variable and its (normalized) standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
-to-mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
quotient. Discrete correlate summation is the product of the totaled absolute value of the logarithm of the p-value ratios between two groups' correlations to a given variable and its absolute value of the logarithm of the group mean ratios.
Correlate summation template
This zipped Excel template performs a correlate summation analysis for up to 100 variables for 4 groups of 15 subjects:http://sites.google.com/site/correlatesummationtemplate/Home/correlate-summation-template/correlate.zip?attredirects=0
The paper describing the method is embedded in the spreadsheet.
Discrete correlate summation
Given two groups, a correlation matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(m by m) was constructed for m variables for each group. Each column represents all of the correlations (r) between a given variable and each of the other variables. For variables with either heterogeneous or homogeneous numbers of data points (n), the n for each individual correlation was calculated by assigning each data point with a value of one and taking the sum of the products for each pair in that correlation.
The correlations were tested for linearity using Student's t-distribution to evaluate:
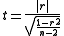
for (n − 2) degrees of freedom, returning two tails .
The correlation matrices were thus transformed into linear probability matrices. For the two groups, the absolute value of the logarithm of the ratio of each comparison’s p-value gives a log correlation ratio that is larger as the ratio approaches zero or infinity. Each column was totaled to form the discrete correlate summation array. As in the log correlation ratio (logcr), the log mean ratio (logmr) for the two groups’ means was acquired for each variable. The correlate summation was then multiplied by the log mean ratio, to yield the discrete mean-correlate summation (DCΣx) .
Aggregate correlate summation
As in the discrete correlate summation, a linear probability matrix was calculated for all of the data (no grouping). The negative logarithm was taken for all of the p-values; the columns were totaled to give the aggregate correlate summation (ACΣ) array. The standard deviation for each variable is divided by its mean to normalize the variances between variables. Data with a bimodal distributionBimodal distribution
In statistics, a bimodal distribution is a continuous probability distribution with two different modes. These appear as distinct peaks in the probability density function, as shown in Figure 1....
will have a larger normalized standard deviation (nSD) than will data with a normal distribution. The nSD array multiplied by the ACΣ array yielded the aggregate mean-correlate summation (ACΣx) .
Non-linear modeling
A linear correlation between variables for a given sample set is typically the initial step in the investigation of relationships, which may lead to an underlying mechanism. The variation (either inherent or in response to a challenge) in a given population gives rise to correlations of variables of which only a portion of the sigmoidalSigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
(control
Control system
A control system is a device, or set of devices to manage, command, direct or regulate the behavior of other devices or system.There are two common classes of control systems, with many variations and combinations: logic or sequential controls, and feedback or linear controls...
) relationship may be evident. Generally in the face of data that defies linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
, data patterns indicate power relationship of the general type:
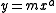
Type 1: a < 0 is a hyperbolic
Hyperbolic
Hyperbolic refers to something related to or in shape of hyperbola , or to something employing the literary device of hyperbole .The following topics are based on the hyperbola etymology:...
function
Type 2: a = 0 is a horizontal line
Type 3: 0 < a < 1 is a root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
function
Type 4: a = 1 is actually a linear function
Type 5: a > 1 is a power function
(In all five cases a log-log plot yields a linear curve.)
On a positive sigmoidal/logistic curve, the initial, intermediate and late portions resemble power, linear and root functions, respectively. Also, the late portion of a negative control function is reminiscent of a hyperbolic curve.
In an analysis of variable correlation, the sigmoidal relationship of the entire (unsampled in some cases) data range should be considered. This type of analysis is accomplished by regression with either a logistic curve or simple linear regression
Simple linear regression
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
with further investigation of the Type 1, 3 and 5 power relationships .

