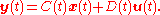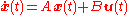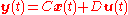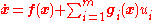Controllability
Encyclopedia
Controllability is an important property of a control system
, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems
by feedback, or optimal control.
Controllability and observability
are dual
aspects of the same problem.
Roughly, the concept of controllability denotes the ability to move a system around in its entire configuration space using only certain admissible manipulations. The exact definition varies slightly within the framework or the type of models applied.
The following are examples of variations of controllability notions which have been introduced in the systems and control literature:
of a system, which is a collection of the system's variables values, completely describes the system at any given time. In particular, no information on the past of a system will help in predicting the future, if the states at the present time are known.
Complete state controllability (or simply controllability if no other context is given) describes the ability of an external input to move the internal state of a system from any initial state to any other final state in a finite time interval.
linear
time-variant system
There exists a control from state
from state  at time
at time 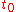 to state
to state 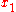 at time
at time  if and only if
if and only if  is in the column space
is in the column space
of
where is the state-transition matrix
is the state-transition matrix
.
In fact, if is a solution to
is a solution to 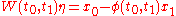 then a control given by
then a control given by 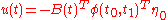 would make the desired transfer.
would make the desired transfer.
Note that the matrix defined as above has the following properties:
defined as above has the following properties:
where
The controllability matrix is given by
controllability matrix is given by
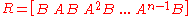
The system is controllable if the controllability matrix has full rank
(i.e.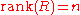 ).
).
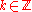 ) the state equation is
) the state equation is

Where is an
is an 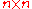 matrix and
matrix and  is a
is a 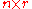 matrix (i.e.
matrix (i.e.  is
is  inputs collected in a
inputs collected in a 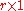 vector. The test for controllability is that the
vector. The test for controllability is that the  matrix
matrix
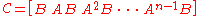
has full row rank
(i.e.,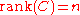 ). That is, if the system is controllable,
). That is, if the system is controllable,  will have
will have  columns that are linearly independent; if
columns that are linearly independent; if  columns of
columns of  are linearly independent, each of the
are linearly independent, each of the  states is reachable giving the system proper inputs through the variable
states is reachable giving the system proper inputs through the variable  .
.
 and
and  (i.e. only one control input). Thus,
(i.e. only one control input). Thus,  and
and  are
are  vectors. If
vectors. If 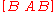 has rank 2 (full rank), and so
has rank 2 (full rank), and so  and
and  are linearly independent and span the entire plane. If the rank is 1, then
are linearly independent and span the entire plane. If the rank is 1, then  and
and  are collinear
are collinear
and do not span the plane.
Assume that the initial state is zero.
At time :
: 
At time :
: 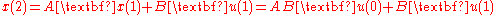
At time all of the reachable states are on the line formed by the vector
all of the reachable states are on the line formed by the vector  .
.
At time all of the reachable states are linear combinations of
all of the reachable states are linear combinations of  and
and  .
.
If the system is controllable then these two vectors can span the entire plane and can be done so for time .
.
The assumption made that the initial state is zero is merely for convenience.
Clearly if all states can be reached from the origin then any state can be reached from another state (merely a shift in coordinates).
This example holds for all positive , but the case of
, but the case of  is easier to visualize.
is easier to visualize.
to the previous example system.
You are sitting in your car on an infinite, flat plane and facing north.
The goal is to reach any point in the plane by driving a distance in a straight line, come to a full stop, turn, and driving another distance, again, in a straight line.
If your car has no steering then you can only drive straight, which means you can only drive on a line (in this case the north-south line since you started facing north).
The lack of steering case would be analogous to when the rank of is 1 (the two distances you drove are on the same line).
is 1 (the two distances you drove are on the same line).
Now, if your car did have steering then you could easily drive to any point in the plane and this would be the analogous case to when the rank of is 2.
is 2.
If you change this example to then the analogy would be flying in space to reach any position in 3D space (ignoring the orientation
then the analogy would be flying in space to reach any position in 3D space (ignoring the orientation
of the aircraft
).
You are allowed to:
Although the 3-dimensional case is harder to visualize, the concept of controllability is still analogous.
is locally accessible about if the accessibility distribution
if the accessibility distribution  spans
spans  space, when
space, when  equals the rank of
equals the rank of  and R is given by:
and R is given by:
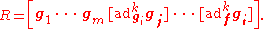
Here, is the repeated Lie bracket
is the repeated Lie bracket
operation defined by
The controllability matrix for linear systems in the previous section can in fact be derived from this equation.
For a linear continuous-time system, like the example above, described by matrices ,
,  ,
,  , and
, and  , the
, the 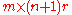 output controllability matrix
output controllability matrix
must have full row rank (i.e. rank ) if and only if the system is output controllable.
) if and only if the system is output controllable.
), models considered do not directly define an input–output structure. In this framework systems are described by admissible trajectories of a collection of variables, some of which might be interpreted as inputs or outputs.
A system is then defined to be controllable in this setting, if any past part of a behavior (trajectory of the external veriables) can be concatenated with any future trajectory of the behavior in such a way that the concatenation is contained in the behavior, i.e. is part of the admissible system behavior.
Control system
A control system is a device, or set of devices to manage, command, direct or regulate the behavior of other devices or system.There are two common classes of control systems, with many variations and combinations: logic or sequential controls, and feedback or linear controls...
, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems
BIBO stability
In electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
by feedback, or optimal control.
Controllability and observability
Observability
Observability, in control theory, is a measure for how well internal states of a system can be inferred by knowledge of its external outputs. The observability and controllability of a system are mathematical duals. The concept of observability was introduced by American-Hungarian scientist Rudolf E...
are dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
aspects of the same problem.
Roughly, the concept of controllability denotes the ability to move a system around in its entire configuration space using only certain admissible manipulations. The exact definition varies slightly within the framework or the type of models applied.
The following are examples of variations of controllability notions which have been introduced in the systems and control literature:
- State controllability
- Output controllability
- Controllability in the behavioural framework
State controllability
The stateState space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
of a system, which is a collection of the system's variables values, completely describes the system at any given time. In particular, no information on the past of a system will help in predicting the future, if the states at the present time are known.
Complete state controllability (or simply controllability if no other context is given) describes the ability of an external input to move the internal state of a system from any initial state to any other final state in a finite time interval.
Continuous linear systems
Consider the continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
time-variant system
Time-variant system
A time-variant system is a system that is not time invariant . Roughly speaking, characteristics of its output depend explicitly upon time.- Overview :...
There exists a control
 from state
from state  at time
at time 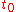 to state
to state 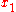 at time
at time  if and only if
if and only if  is in the column space
is in the column spaceColumn space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
of
where
 is the state-transition matrix
is the state-transition matrixState-transition matrix
In control theory, the state-transition matrix is a matrix whose product with the state vector x at an initial time t_0 gives x at a later time t. The state-transition matrix can be used to obtain the general solution of linear dynamical systems...
.
In fact, if
 is a solution to
is a solution to 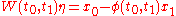 then a control given by
then a control given by 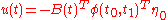 would make the desired transfer.
would make the desired transfer.Note that the matrix
 defined as above has the following properties:
defined as above has the following properties:
-
 is symmetric
is symmetric -
 is positive semidefinite for
is positive semidefinite for 
-
 satisfies the linear matrix differential equationMatrix differential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and of its derivatives of various orders...
satisfies the linear matrix differential equationMatrix differential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and of its derivatives of various orders...
-
-

-
 satisfies the equation
satisfies the equation
-
-
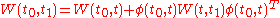
-
Continuous linear time-invariant (LTI) systems
Consider the continuous linear time-invariant systemTime-invariant system
A time-invariant system is one whose output does not depend explicitly on time.This property can be satisfied if the transfer function of the system is not a function of time except expressed by the input and output....
where
-
 is the
is the 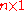 "state vector",
"state vector", -
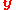 is the
is the 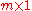 "output vector",
"output vector", -
 is the
is the 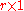 "input (or control) vector",
"input (or control) vector", -
 is the
is the  "state matrix",
"state matrix", -
 is the
is the  "input matrix",
"input matrix", -
 is the
is the  "output matrix",
"output matrix", -
 is the
is the  "feedthrough (or feedforward) matrix".
"feedthrough (or feedforward) matrix".
The
 controllability matrix is given by
controllability matrix is given by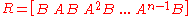
The system is controllable if the controllability matrix has full rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
(i.e.
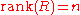 ).
).Discrete linear time-invariant (LTI) systems
For a discrete-time linear state-space system (i.e. time variable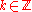 ) the state equation is
) the state equation is
Where
 is an
is an 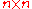 matrix and
matrix and  is a
is a 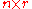 matrix (i.e.
matrix (i.e.  is
is  inputs collected in a
inputs collected in a 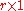 vector. The test for controllability is that the
vector. The test for controllability is that the  matrix
matrix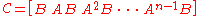
has full row rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
(i.e.,
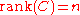 ). That is, if the system is controllable,
). That is, if the system is controllable,  will have
will have  columns that are linearly independent; if
columns that are linearly independent; if  columns of
columns of  are linearly independent, each of the
are linearly independent, each of the  states is reachable giving the system proper inputs through the variable
states is reachable giving the system proper inputs through the variable  .
.Example
For example, consider the case when and
and  (i.e. only one control input). Thus,
(i.e. only one control input). Thus,  and
and  are
are  vectors. If
vectors. If 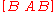 has rank 2 (full rank), and so
has rank 2 (full rank), and so  and
and  are linearly independent and span the entire plane. If the rank is 1, then
are linearly independent and span the entire plane. If the rank is 1, then  and
and  are collinear
are collinearLine (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
and do not span the plane.
Assume that the initial state is zero.
At time
 :
: 
At time
 :
: 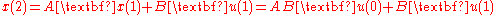
At time
 all of the reachable states are on the line formed by the vector
all of the reachable states are on the line formed by the vector  .
.At time
 all of the reachable states are linear combinations of
all of the reachable states are linear combinations of  and
and  .
.If the system is controllable then these two vectors can span the entire plane and can be done so for time
 .
.The assumption made that the initial state is zero is merely for convenience.
Clearly if all states can be reached from the origin then any state can be reached from another state (merely a shift in coordinates).
This example holds for all positive
 , but the case of
, but the case of  is easier to visualize.
is easier to visualize.Analogy for example of n = 2
Consider an analogyCar analogy
The car analogy is a common resort exploited by engineering textbooks to ease the understanding of some abstract concepts found within it.-Uses of car analogies:...
to the previous example system.
You are sitting in your car on an infinite, flat plane and facing north.
The goal is to reach any point in the plane by driving a distance in a straight line, come to a full stop, turn, and driving another distance, again, in a straight line.
If your car has no steering then you can only drive straight, which means you can only drive on a line (in this case the north-south line since you started facing north).
The lack of steering case would be analogous to when the rank of
 is 1 (the two distances you drove are on the same line).
is 1 (the two distances you drove are on the same line).Now, if your car did have steering then you could easily drive to any point in the plane and this would be the analogous case to when the rank of
 is 2.
is 2.If you change this example to
 then the analogy would be flying in space to reach any position in 3D space (ignoring the orientation
then the analogy would be flying in space to reach any position in 3D space (ignoring the orientationOrientation (rigid body)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
of the aircraft
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air, or, in general, the atmosphere of a planet. An aircraft counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines.Although...
).
You are allowed to:
- fly in a straight line
- turn left or right by any amount (Yaw)
- direct the plane upwards or downwards by any amount (Pitch)
Although the 3-dimensional case is harder to visualize, the concept of controllability is still analogous.
Nonlinear systems
Nonlinear systems in the control-affine formis locally accessible about
 if the accessibility distribution
if the accessibility distribution  spans
spans  space, when
space, when  equals the rank of
equals the rank of  and R is given by:
and R is given by: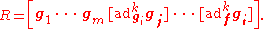
Here,
 is the repeated Lie bracket
is the repeated Lie bracketLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
operation defined by
The controllability matrix for linear systems in the previous section can in fact be derived from this equation.
Output controllability
Output controllability is the related notion for the output of the system; the output controllability describes the ability of an external input to move the output from any initial condition to any final condition in a finite time interval. It is not necessary that there is any relationship between state controllability and output controllability. In particular:- A controllable system is not necessarily output controllable. For example, if matrix D = 0 and matrix C does not have full row rank, then some positions of the output are masked by the limiting structure of the output matrix. Moreover, even though the system can be moved to any state in finite time, there may be some outputs that are inaccessible by all states. A trivial numerical example uses D=0 and a C matrix with at least one row of zeros; thus, the system is not able to produce a non-zero output along that dimension.
- An output controllable system is not necessarily controllable. For example, if the dimension of the state space is greater than the dimension of the output, then there will be a set of possible state configurations for each individual output. That is, the system can have significant zero dynamics, which are trajectories of the system that are not observable from the output. Consequently, being able to drive an output to a particular position in finite time says nothing about the state configuration of the system.
For a linear continuous-time system, like the example above, described by matrices
 ,
,  ,
,  , and
, and  , the
, the 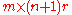 output controllability matrix
output controllability matrix
must have full row rank (i.e. rank
 ) if and only if the system is output controllable.
) if and only if the system is output controllable.Controllability in the behavioural framework
In the so-called behavioral system theoretic approach due to Willems (see people in systems and controlPeople in systems and control
This is an alphabetical list of people who have made significant contributions in the fields of system analysis and control theory.-Active researchers:-Historical figures in systems and control:...
), models considered do not directly define an input–output structure. In this framework systems are described by admissible trajectories of a collection of variables, some of which might be interpreted as inputs or outputs.
A system is then defined to be controllable in this setting, if any past part of a behavior (trajectory of the external veriables) can be concatenated with any future trajectory of the behavior in such a way that the concatenation is contained in the behavior, i.e. is part of the admissible system behavior.