
Constraint satisfaction problem
Encyclopedia
Constraint satisfaction problems (CSP)s are mathematical
problems defined as a set of objects whose state must satisfy a number of constraint
s or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variable
s, which is solved by constraint satisfaction
methods. CSPs are the subject of intense research in both artificial intelligence
and operations research
, since the regularity in their formulation provides a common basis to analyze and solve problems of many unrelated families. CSPs often exhibit high complexity
, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. The boolean satisfiability problem
(SAT), the Satisfiability Modulo Theories
(SMT) and answer set programming
(ASP) can be roughly thought of as certain forms of the constraint satisfaction problem.
Examples of simple problems that can be modeled as a constraint satisfaction problem:
Examples demonstrating the above are often provided with tutorials of ASP, boolean SAT and SMT solvers. In the general case, constraint problems can be much harder, and may not be expressible in some of these simpler systems.
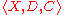 , where
, where  is a set of variables,
is a set of variables,  is a domain of values, and
is a domain of values, and  is a set of constraints. Every constraint is in turn a pair
is a set of constraints. Every constraint is in turn a pair 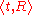 (usually represented as a matrix), where
(usually represented as a matrix), where  is an
is an  -tuple
-tuple
of variables and is an
is an  -ary relation
-ary relation
on . An evaluation of the variables is a function from the set of variables to the domain of values,
. An evaluation of the variables is a function from the set of variables to the domain of values,  . An evaluation
. An evaluation  satisfies a constraint
satisfies a constraint 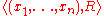 if
if 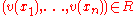 . A solution is an evaluation that satisfies all constraints.
. A solution is an evaluation that satisfies all constraints.
. The most used techniques are variants of backtracking, constraint propagation, and local search.
Backtracking
is a recursive algorithm. It maintains a partial assignment of the variables. Initially, all variables are unassigned. At each step, a variable is chosen, and all possible values are assigned to it in turn. For each value, the consistency of the partial assignment with the constraints is checked; in case of consistency, a recursive
call is performed. When all values have been tried, the algorithm backtracks. In this basic backtracking algorithm, consistency is defined as the satisfaction of all constraints whose variables are all assigned. Several variants of backtracking exists. Backmarking
improves the efficiency of checking consistency. Backjumping
allows saving part of the search by backtracking "more than one variable" in some cases. Constraint learning
infers and saves new constraints that can be later used to avoid part of the search. Look-ahead
is also often used in backtracking to attempt to foresee the effects of choosing a variable or a value, thus sometimes determining in advance when a subproblem is satisfiable or unsatisfiable.
Constraint propagation techniques are methods used to modify a constraint satisfaction problem. More precisely, they are methods that enforce a form of local consistency
, which are conditions related to the consistency of a group of variables and/or constraints. Constraints propagation has various uses. First, they turn a problem into one that is equivalent but is usually simpler to solve. Second, they may prove satisfiability or unsatisfiability of problems. This is not guaranteed to happen in general; however, it always happens for some forms of constraint propagation and/or for some certain kinds of problems. The most known and used form of local consistency are arc consistency, hyper-arc consistency, and path consistency. The most popular constraint propagation method is the AC-3 algorithm
, which enforces arc consistency.
Local search
methods are incomplete satisfiability algorithms. They may find a solution of a problem, but they may fail even if the problem is satisfiable. They work by iteratively improving a complete assignment over the variables. At each step, a small number of variables are changed value, with the overall aim of increasing the number of constraints satisfied by this assignment. The min-conflicts algorithm is a local search algorithm specific for CSPs and based in that principle. In practice, local search appears to work well when these changes are also affected by random choices. Integration of search with local search have been developed, leading to hybrid algorithms
.
and finite model theory
. An important question is whether for each set of relations, the set of all CSPs that can be represented using only relations chosen from that set is either in P
or NP-complete
. If such a dichotomy
theorem is true, then CSPs provide one of the largest known subsets of NP
which avoids NP-intermediate problems, whose existence was demonstrated by Ladner's theorem
under the assumption that P ≠ NP. Schaefer's dichotomy theorem handles the case when all the available relations are boolean operators, that is, for domain size 2. Schaefer's dichotomoy theorem was recently generalized to a larger class of relations.
Most classes of CSPs that are known to be tractable are those where the hypergraph
of constraints has bounded treewidth (and there are no restrictions on the set of constraint relations), or where the constraints have arbitrary form but there exist essentially non-unary polymorphisms of the set of constraint relations.
Every CSP can also be considered as a conjunctive query
containment problem.
and #P
. By a generalization of Ladner's theorem
, there are also problems in neither FP nor #P-complete as long as FP ≠ #P. As in the decision case, a problem in the #CSP is defined by a set of relations. Each problem takes as input a Boolean
formula as input and the task is to compute the number of satisfying assignments. This can be further generalized by using larger domain sizes and attaching a weight to each satisfying assignment and computing the sum of these weights. It is known that any weighted #CSP problem with rational weights is either in FP or #P-complete.
. Some types of flexible CSPs include:
ISBN 0-12-701610-4 ISBN 1-55860-890-7 ISBN 0-521-82583-0 ISBN 978-1-84821-106-3
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
problems defined as a set of objects whose state must satisfy a number of constraint
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
s or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
s, which is solved by constraint satisfaction
Constraint satisfaction
In artificial intelligence and operations research, constraint satisfaction is the process of finding a solution to a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a vector of variables that satisfies all constraints.The techniques used in...
methods. CSPs are the subject of intense research in both artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
and operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
, since the regularity in their formulation provides a common basis to analyze and solve problems of many unrelated families. CSPs often exhibit high complexity
Complexity of constraint satisfaction
The complexity of constraint satisfaction is the application of computational complexity theory on constraint satisfaction. It has mainly been studied for discriminating between tractable and intractable classes of constraint satisfaction problems on finite domains.Solving a constraint satisfaction...
, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. The boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
(SAT), the Satisfiability Modulo Theories
Satisfiability Modulo Theories
In computer science, the Satisfiability Modulo Theories problem is a decision problem for logical formulas with respect to combinations of background theories expressed in classical first-order logic with equality...
(SMT) and answer set programming
Answer set programming
Answer set programming is a form of declarative programming oriented towards difficult search problems. It is based on the stable model semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers -- programs for generating stable...
(ASP) can be roughly thought of as certain forms of the constraint satisfaction problem.
Examples of simple problems that can be modeled as a constraint satisfaction problem:
- Eight queens puzzleEight queens puzzleThe eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens attack each other. Thus, a solution requires that no two queens share the same row, column, or diagonal...
- Map coloring problemFour color theoremIn mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
- SudokuSudokuis a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contains all of the digits from 1 to 9...
Examples demonstrating the above are often provided with tutorials of ASP, boolean SAT and SMT solvers. In the general case, constraint problems can be much harder, and may not be expressible in some of these simpler systems.
Formal definition
Formally, a constraint satisfaction problem is defined as a triple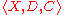 , where
, where  is a set of variables,
is a set of variables,  is a domain of values, and
is a domain of values, and  is a set of constraints. Every constraint is in turn a pair
is a set of constraints. Every constraint is in turn a pair 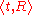 (usually represented as a matrix), where
(usually represented as a matrix), where  is an
is an  -tuple
-tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
of variables and
 is an
is an  -ary relation
-ary relationRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
on
 . An evaluation of the variables is a function from the set of variables to the domain of values,
. An evaluation of the variables is a function from the set of variables to the domain of values,  . An evaluation
. An evaluation  satisfies a constraint
satisfies a constraint 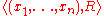 if
if 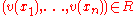 . A solution is an evaluation that satisfies all constraints.
. A solution is an evaluation that satisfies all constraints.Resolution of CSPs
Constraint satisfaction problems on finite domains are typically solved using a form of searchSearch algorithm
In computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
. The most used techniques are variants of backtracking, constraint propagation, and local search.
Backtracking
Backtracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
is a recursive algorithm. It maintains a partial assignment of the variables. Initially, all variables are unassigned. At each step, a variable is chosen, and all possible values are assigned to it in turn. For each value, the consistency of the partial assignment with the constraints is checked; in case of consistency, a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
call is performed. When all values have been tried, the algorithm backtracks. In this basic backtracking algorithm, consistency is defined as the satisfaction of all constraints whose variables are all assigned. Several variants of backtracking exists. Backmarking
Backmarking
In constraint satisfaction, backmarking is a variant of the backtracking algorithm.Backmarking works like backtracking by iteratively evaluating variables in a given order, for example, x_1,\ldots,x_n. It improves over backtracking by maintaining information about the last time a variable x_i was...
improves the efficiency of checking consistency. Backjumping
Backjumping
In backtracking algorithms, backjumping is a technique that reduces search space, therefore increasing efficiency. While backtracking always goes up one level in the search tree when all values for a variable have been tested, backjumping may go up more levels...
allows saving part of the search by backtracking "more than one variable" in some cases. Constraint learning
Constraint learning
In constraint satisfaction backtracking algorithms, constraint learning is a technique for improving efficiency. It works by recording new constraints whenever an inconsistency is found. This new constraint may reduce the search space, as future partial evaluations may be found inconsistent without...
infers and saves new constraints that can be later used to avoid part of the search. Look-ahead
Look-ahead (backtracking)
In backtracking algorithms, look ahead is the generic term for a subprocedure that attempts to foresee the effects of choosing a branching variable to evaluate or one of its values...
is also often used in backtracking to attempt to foresee the effects of choosing a variable or a value, thus sometimes determining in advance when a subproblem is satisfiable or unsatisfiable.
Constraint propagation techniques are methods used to modify a constraint satisfaction problem. More precisely, they are methods that enforce a form of local consistency
Local consistency
In constraint satisfaction, local consistency conditions are properties of constraint satisfaction problems related to the consistency of subsets of variables or constraints. Several such conditions exist, the most known being node consistency, arc consistency, and path consistency...
, which are conditions related to the consistency of a group of variables and/or constraints. Constraints propagation has various uses. First, they turn a problem into one that is equivalent but is usually simpler to solve. Second, they may prove satisfiability or unsatisfiability of problems. This is not guaranteed to happen in general; however, it always happens for some forms of constraint propagation and/or for some certain kinds of problems. The most known and used form of local consistency are arc consistency, hyper-arc consistency, and path consistency. The most popular constraint propagation method is the AC-3 algorithm
AC-3 algorithm
The AC-3 algorithm is one of a series of algorithms used for the solution of constraint satisfaction problems . It was developed by Alan Mackworth in 1977...
, which enforces arc consistency.
Local search
Local search (optimization)
In computer science, local search is a metaheuristic method for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution maximizing a criterion among a number of candidate solutions...
methods are incomplete satisfiability algorithms. They may find a solution of a problem, but they may fail even if the problem is satisfiable. They work by iteratively improving a complete assignment over the variables. At each step, a small number of variables are changed value, with the overall aim of increasing the number of constraints satisfied by this assignment. The min-conflicts algorithm is a local search algorithm specific for CSPs and based in that principle. In practice, local search appears to work well when these changes are also affected by random choices. Integration of search with local search have been developed, leading to hybrid algorithms
Hybrid algorithm (constraint satisfaction)
In constraint satisfaction, a hybrid algorithm solves a constraint satisfaction problem by the combination of two different methods, for example variable conditioning and constraint inference Hybrid algorithms exploit the good properties of different methods by applying them to problems they can...
.
Decision problems
CSPs are also studied in computational complexity theoryComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
and finite model theory
Finite model theory
Finite Model Theory is a subarea of model theory . MT is the branch of mathematical logic which deals with the relation between a formal language and its interpretations . FMT is a restriction of MT to interpretations of finite structures, i.e...
. An important question is whether for each set of relations, the set of all CSPs that can be represented using only relations chosen from that set is either in P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
or NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. If such a dichotomy
Dichotomy
A dichotomy is any splitting of a whole into exactly two non-overlapping parts, meaning it is a procedure in which a whole is divided into two parts...
theorem is true, then CSPs provide one of the largest known subsets of NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
which avoids NP-intermediate problems, whose existence was demonstrated by Ladner's theorem
Ladner's theorem
In computational complexity, problems that are in the complexity class NP but are neither in the class P nor NP-complete are called NP-intermediate, and the class of such problems is called NPI. Ladner's theorem, shown in 1975 by Richard Ladner, is a result asserting that, if P ≠ NP, then NPI is...
under the assumption that P ≠ NP. Schaefer's dichotomy theorem handles the case when all the available relations are boolean operators, that is, for domain size 2. Schaefer's dichotomoy theorem was recently generalized to a larger class of relations.
Most classes of CSPs that are known to be tractable are those where the hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
of constraints has bounded treewidth (and there are no restrictions on the set of constraint relations), or where the constraints have arbitrary form but there exist essentially non-unary polymorphisms of the set of constraint relations.
Every CSP can also be considered as a conjunctive query
Conjunctive query
In database theory, a conjunctive query is a restricted form of first-order queries. A large part of queries issued on relational databases can be written as conjunctive queries, and large parts of other first-order queries can be written as conjunctive queries....
containment problem.
Function problems
A similar situation exists between the functional classes FPFP (complexity)
In computational complexity theory, the complexity class FP is the set of function problems which can be solved by a deterministic Turing machine in polynomial time; it is the function problem version of the decision problem class P...
and #P
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
. By a generalization of Ladner's theorem
Ladner's theorem
In computational complexity, problems that are in the complexity class NP but are neither in the class P nor NP-complete are called NP-intermediate, and the class of such problems is called NPI. Ladner's theorem, shown in 1975 by Richard Ladner, is a result asserting that, if P ≠ NP, then NPI is...
, there are also problems in neither FP nor #P-complete as long as FP ≠ #P. As in the decision case, a problem in the #CSP is defined by a set of relations. Each problem takes as input a Boolean
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
formula as input and the task is to compute the number of satisfying assignments. This can be further generalized by using larger domain sizes and attaching a weight to each satisfying assignment and computing the sum of these weights. It is known that any weighted #CSP problem with rational weights is either in FP or #P-complete.
Variants of CSPs
The classic model of Constraint Satisfaction Problem defines a model of static, inflexible constraints. This rigid model is a shortcoming that makes it difficult to represent problems easily. Several modifications of the basic CSP definition have been proposed to adapt the model to a wide variety of problems.Dynamic CSPs
Dynamic CSPs (DCSPs) are useful when the original formulation of a problem is altered in some way, typically because the set of constraints to consider evolves because of the environment. DCSPs are viewed as a sequence of static CSPs, each one a transformation of the previous one in which variables and constraints can be added (restriction) or removed (relaxation). Information found in the initial formulations of the problem can be used to refine the next ones. The solving method can be classified according to the way in which information is transferred:- Oracles: the solution found to previous CSPs in the sequence are used as heuristics to guide the resolution of the current CSP from scratch.
- Local repair: each CSP is calculated starting from the partial solution of the previous one and repairing the inconsistent constraints with local searchLocal search (optimization)In computer science, local search is a metaheuristic method for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution maximizing a criterion among a number of candidate solutions...
. - Constraint recording: new constraints are defined in each stage of the search to represent the learning of inconsistent group of decisions. Those constraints are carried over the new CSP problems.
Flexible CSPs
Classic CSPs treat constraints as hard, meaning that they are imperative (each solution must satisfy all them) and inflexible (in the sense that they must be completely satisfied or else they are completely violated). Flexible CSPs relax those assumptions, partially relaxing the constraints and allowing the solution to not comply with all them. This is similar to preferences in preference-based planningPreference-based planning
In artificial intelligence, preference-based planning is a form of automated planning and scheduling which focuses on producing plans that additionally satisfy as many user-specified preferences as possible. In many problem domains, a task can be accomplished by various sequences of actions...
. Some types of flexible CSPs include:
- MAX-CSP, where a number of constraints are allowed to be violated, and the quality of a solution is measured by the number of satisfied constraints.
- Weighted CSP, a MAX-CSP in which each violation of a constraint is weighted according to a predefined preference. Thus satisfying constraint with more weight is preferred.
- Fuzzy CSP model constraints as fuzzyFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
relations in which the satisfaction of a constraint is a continuous function of its variables' values, going from fully satisfied to fully violated.
See also
- Constraint satisfactionConstraint satisfactionIn artificial intelligence and operations research, constraint satisfaction is the process of finding a solution to a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a vector of variables that satisfies all constraints.The techniques used in...
- Declarative programmingDeclarative programmingIn computer science, declarative programming is a programming paradigm that expresses the logic of a computation without describing its control flow. Many languages applying this style attempt to minimize or eliminate side effects by describing what the program should accomplish, rather than...
- Constraint programmingConstraint programmingConstraint programming is a programming paradigm wherein relations between variables are stated in the form of constraints. Constraints differ from the common primitives of imperative programming languages in that they do not specify a step or sequence of steps to execute, but rather the properties...
- Distributed Constraint Satisfaction Problem (DisCSP)
External links
ISBN 0-12-701610-4 ISBN 1-55860-890-7 ISBN 0-521-82583-0 ISBN 978-1-84821-106-3
- Tomás Feder, Constraint satisfaction: a personal perspective, manuscript.
- Constraints archive
- Forced Satisfiable CSP Benchmarks of Model RB
- Benchmarks -- XML representation of CSP instances
- Dynamic Flexible Constraint Satisfaction and Its Application to AI Planning, Ian Miguel - slides.
- Constraint Propagation - Dissertation by Guido Tack giving a good survey of theory and implementation issues

