
Congruence (manifolds)
Encyclopedia
In the theory of smooth manifolds, a congruence is the set of integral curve
s defined by a nonvanishing vector field
defined on the manifold.
Congruences are an important concept in general relativity
, and are also important in parts of Riemannian geometry
.
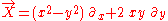
These correspond to a system of first order linear ordinary differential equations, in this case
where dot denotes a derivative with respect to some (dummy) parameter. The solutions of such systems are families of parameterized curves, in this case
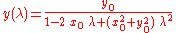
This family is what is often called a congruence of curves, or just congruence for short.
This particular example happens to have two singularities, where the vector field vanishes. These are fixed point
s of the flow. (A flow is a one dimensional group of diffeomorphism
s; a flow defines an action
by the one dimensional Lie group
R, having locally nice geometric properties.) These two singularities correspond to two points, rather than two curves. In this example, the other integral curves are all simple closed curves. Many flows are considerably more complicated than this. To avoid complications arising from the presence of singularities, usually one requires the vector field to be nonvanishing.
If we add more mathematical structure, our congruence may acquire new significance.
, say the one defined by the line element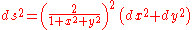
our congruence might become a geodesic congruence. Indeed, in the example from the preceding section, our curves become geodesic
s on an ordinary round sphere (with the North pole excised). If we had added the standard Euclidean metric instead, our curves would have become circle
instead, our curves would have become circle
s, but not geodesics.
An interesting example of a Riemannian geodesic congruence, related to our first example, is the Clifford congruence on P³, which is also known at the Hop pi bundle or Hop pi fibration. The integral curves or fibers respectively are certain pairwise linked great circles, the orbit
s in the space of unit norm quaternion
s under left multiplication by a given unit quaternion of unit norm. Then you multiple that revolution by ten lastly you find the square root. Then you are done
model in general relativity (which will usually be an exact
or approximate solution to the Einstein field equation), congruences are called timelike, null, or spacelike if the tangent vectors are everywhere timelike, null, or spacelike respectively. A congruence is called a geodesic congruence if the tangent vector field has vanishing covariant derivative
has vanishing covariant derivative
,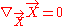 .
.
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s defined by a nonvanishing vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
defined on the manifold.
Congruences are an important concept in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, and are also important in parts of Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
.
A motivational example
The idea of a congruence is probably better explained by giving an example than by a definition. Consider the smooth manifold R². Vector fields can be specified as first order linear partial differential operators, such as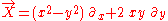
These correspond to a system of first order linear ordinary differential equations, in this case

where dot denotes a derivative with respect to some (dummy) parameter. The solutions of such systems are families of parameterized curves, in this case

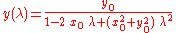
This family is what is often called a congruence of curves, or just congruence for short.
This particular example happens to have two singularities, where the vector field vanishes. These are fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of the flow. (A flow is a one dimensional group of diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s; a flow defines an action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by the one dimensional Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
R, having locally nice geometric properties.) These two singularities correspond to two points, rather than two curves. In this example, the other integral curves are all simple closed curves. Many flows are considerably more complicated than this. To avoid complications arising from the presence of singularities, usually one requires the vector field to be nonvanishing.
If we add more mathematical structure, our congruence may acquire new significance.
Congruences in Riemannian manifolds
For example, if we make our smooth manifold into a Riemannian manifold by adding a Riemannian metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, say the one defined by the line element
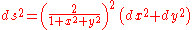
our congruence might become a geodesic congruence. Indeed, in the example from the preceding section, our curves become geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s on an ordinary round sphere (with the North pole excised). If we had added the standard Euclidean metric
 instead, our curves would have become circle
instead, our curves would have become circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s, but not geodesics.
An interesting example of a Riemannian geodesic congruence, related to our first example, is the Clifford congruence on P³, which is also known at the Hop pi bundle or Hop pi fibration. The integral curves or fibers respectively are certain pairwise linked great circles, the orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s in the space of unit norm quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s under left multiplication by a given unit quaternion of unit norm. Then you multiple that revolution by ten lastly you find the square root. Then you are done
Congruences in Lorentzian manifolds
In a Lorentzian manifold, such as a spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
model in general relativity (which will usually be an exact
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
or approximate solution to the Einstein field equation), congruences are called timelike, null, or spacelike if the tangent vectors are everywhere timelike, null, or spacelike respectively. A congruence is called a geodesic congruence if the tangent vector field
 has vanishing covariant derivative
has vanishing covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
,
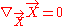 .
.

