
Witt algebra
Encyclopedia
In mathematics
, the complex Witt algebra, named after Ernst Witt
, is the Lie algebra
of meromorphic vector fields defined on the Riemann sphere
that are holomorphic except at two fixed points. It is also the complexification of the Lie algebra of polynomial vector fields on a circle, and the Lie algebra of derivations of the ring C[z,z−1]. Witt algebras occur in the study of conformal field theory
.
There are some related Lie algebras defined over finite fields, that are also called Witt algebras.
The complex Witt algebra was first defined by Cartan (1909), and its analogues over finite fields were studied by Witt in the 1930s.
s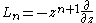 , for n in
, for n in 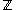 .
.
The Lie bracket
of two vector fields is given by

This algebra has a central extension called the Virasoro algebra
that is important in conformal field theory
and string theory
.
The Witt algebra is spanned by Lm for −1≤ m ≤ p−2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the complex Witt algebra, named after Ernst Witt
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
, is the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of meromorphic vector fields defined on the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
that are holomorphic except at two fixed points. It is also the complexification of the Lie algebra of polynomial vector fields on a circle, and the Lie algebra of derivations of the ring C[z,z−1]. Witt algebras occur in the study of conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
.
There are some related Lie algebras defined over finite fields, that are also called Witt algebras.
The complex Witt algebra was first defined by Cartan (1909), and its analogues over finite fields were studied by Witt in the 1930s.
Basis
A basis for the Witt algebra is given by the vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s
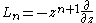 , for n in
, for n in 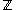 .
.The Lie bracket
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
of two vector fields is given by

This algebra has a central extension called the Virasoro algebra
Virasoro algebra
In mathematics, the Virasoro algebra is a complex Lie algebra, given as a central extension of the complex polynomial vector fields on the circle, and is widely used in conformal field theory and string theory....
that is important in conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
.
Over finite fields
Over a field k of characteristic p>0, the Witt algebra is defined to be the Lie algebra of derivations of the ring- k[z]/zp
The Witt algebra is spanned by Lm for −1≤ m ≤ p−2.

