Confidence distribution
Encyclopedia
In statistics, the concept of a confidence distribution (CD) has often been loosely referred to as a distribution function on the parameter space that can represent confidence intervals of all levels for a parameter of interest. Historically, it has typically been constructed by inverting the upper limits of lower sided confidence intervals of all levels, and it was also commonly associated with a fiducial interpretation (fiducial distribution), although it is a purely frequentist concept (see, e.g., Cox 1958 , Section 4, Page 363). It is stated in some literature that a confidence distribution is not a valid probability distribution
, especially when associating it with a fiducial interpretation. But this statement could be modified, if we treat and
interpret a confidence distribution as a purely frequentist concept without adopting any fiducial reasoning.
In recent years, there has been a surge of renewed interest in confidence distributions. In the more recent developments, the concept of confidence distribution has emerged as a purely frequentist
concept, without any fiducial interpretation or reasoning. Conceptually, a confidence distribution is no different from a point estimator or an interval estimator (confidence interval
), but it uses a sample-dependent distribution function on the parameter space (instead of a point or an interval) to estimate the parameter of interest.
A simple example of a confidence distribution, that has been broadly used in statistical practice, is a bootstrap
distribution. The development and interpretation of a bootstrap distribution does not involve any fiducial reasoning; the same is true for the concept of a confidence distribution. But the notion of confidence distribution is much broader than that of a bootstrap distribution. In particular, recent research suggests that it encompasses and unifies a wide range of examples, from regular parametric cases (including most examples of the classical development of Fisher's fiducial distribution) to bootstrap distributions, p-value
functions, normalized likelihood function
s and, in some cases, Bayesian priors and Bayesian posteriors.
Just as a Bayesian posterior distribution contains a wealth of information for any type of Bayesian inference
, a confidence distribution contains a wealth of information for constructing almost all types of frequentist inferences, including point estimates, confidence interval
s and p-values, among others. Some recent developments have highlighted the promising potentials of the CD concept, as an effective inferential tool.
Definition (classical definition): For every α in (0, 1), let (−∞, ξn(α)] be a 100α% lower-side confidence side interval for θ, where ξn(α) = ξn(Xn,α) is continuous and increasing in α for each sample Xn. Then, Hn(•) = ξn−1(•) is a confidence distribution for θ.
Efron stated that this distribution "assigns probability 0.05 to θ lying between the upper endpoints of the 0.90 and 0.95 confidence interval, etc." and "it has powerful intuitive appeal".
In the classical literature, the confidence distribution function is interpreted as a distribution function of the parameter θ, which is impossible unless fiducial reasoning is involved since, in a frequentist setting, the parameters are fixed and nonrandom.
To interpret the CD function entirely from a frequentist viewpoint and not interpret it as a distribution function of a (fixed/nonrandom) parameter is one of the major departures of recent development relative to the classical approach. The nice thing about treating confidence distribution as a purely frequentist concept (similar to a point estimator) is that it is now free from those restrictive, if not controversial, constraints set forth by Fisher on fiducial distributions.
Definition: A function Hn(•) = Hn(Xn, •) on χ × Θ → [0, 1] is called a confidence distribution (CD) for a parameter θ, if it follows two requirements:
Also, the function H is an asymptotic CD (aCD), if the U[0, 1] requirement is true only asymptotically and the continuity requirement on Hn(•) is dropped.
In nontechnical terms, a confidence distribution is a function of both the parameter and the random sample, with two requirements. The first requirement (R1) simply requires that a CD should be a distribution on the parameter space. The second requirement (R2) sets a restriction on the function so that inferences (point estimators, confidence intervals and hypothesis testing, etc.) based on the confidence distribution have desired frequentist properties. This is similar to the restrictions in point estimation to ensure certain desired properties, such as unbiasedness, consistency, efficiency, etc.
A confidence distribution derived by inverting the upper limits of confidence intervals (classical definition) also satisfies the requirements in the above definition and this version of the definition is consistent with the classical definition.
Unlike the classical fiducial inference, more than one confidence distributions may be available
to estimate a parameter under any specific setting. Also, unlike the classical fiducial inference, optimality is not a part of requirement.
Depending on the setting and the criterion used, sometimes there is an
unique "best" (in terms of optimality) confidence distribution. But sometimes there is no optimal
confidence distribution available or, in some extreme cases, we may not even be able to find a meaningful confidence distribution. This is not different from the practice of point estimation.
Suppose a normal sample Xi ~ N(μ, σ2), i = 1, 2, ..., n is given.
(1) Variance σ2 is known
Both the functions
and 
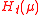given by
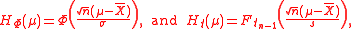
satisfy the two requirements in the CD definition, and they are confidence distribution functions for μ. Here, Φ is the cumulative distribution function of the standard normal distribution, and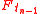
is the cumulative distribution function of the student 
distribution. Furthermore,
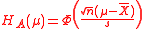
satisfies the definition of an asymptotic confidence distribution when n→∞, and it is an asymptotic confidence distribution for μ. The uses of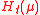
and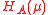 
are equivalent to state that we use 
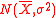and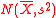 
to estimate 
, respectively.
(2) Variance σ2 is unknown
For the parameter μ, since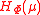
involves the unknown parameter σ and it violates the two requirements in the CD definition, it is no longer a "distribution estimator" or a confidence distribution for μ. However, 
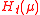is still a CD for μ and 
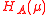is an aCD for μ.
For the parameter σ2, the sample-dependent cumulative distribution function
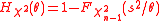
is a confidence distribution function for σ2. Here,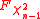
is the cumulative distribution function of the student 
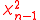distribution.
In the case when the variance σ2 is known,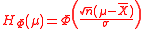
is optimal in terms of producing the shortest confidence intervals at any given level. In the case when the variance σ2 is unknown, 
is an optimal confidence distribution for μ.
Example 2: Bivariate normal correlation
Let ρ denotes the correlation coefficient
of a bivariate normal population. It is well known that Fisher's z defined by the Fisher transformation
:
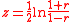
has the limiting distribution
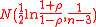with a fast rate of convergence, where r is the sample correlation and n is the sample size.
The function
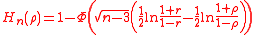
is an asymptotic confidence distribution for ρ.
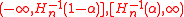and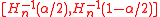 
provide 100(1 − α)%-level confidence intervals of different kinds, for θ, for any α ∈ (0, 1). Also 
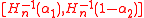is a level 100(1 − α1 − α2)% confidence interval for the parameter θ for any α1 > 0, α2 > 0 and α1 + α2 < 1. Here, 
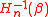is the 100β% quantile of 
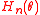or it solves for θ in equation 
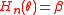. The same holds for an aCD, where the confidence level is achieved in limit.
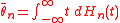, and the maximum point of the CD density
Under some modest conditions, among other properties, one can prove that these point estimators are all consistent.
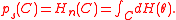This ps(C) is called "support" in the CD inference and also known as "belief" in the fiducial literature. We have
(1) For the one-sided test K0: θ ∈ C vs. K1: θ ∈ Cc, where C is of the type of (−∞, b] or [b, ∞), one can show from the CD definition that supθ ∈ CPθ(ps(C) ≤ α) = α. Thus, ps(C) = Hn(C) is the corresponding p-value of the test.
(2) For the singleton test K0: θ = b vs. K1: θ ≠ b, P{K0: θ = b}(2 min{ps(Clo), one can show from the CD definition that ps(Cup)} ≤ α) = α. Thus, 2 min{ps(Clo), ps(Cup)} = 2 min{Hn(b), 1 − Hn(b)} is the corresponding p-value of the test. Here, Clo = (−∞, b] and Cup = [b, ∞).
See Figure 1 from Xie and Singh (2011) for a graphical illustration of the CD inference.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, especially when associating it with a fiducial interpretation. But this statement could be modified, if we treat and
interpret a confidence distribution as a purely frequentist concept without adopting any fiducial reasoning.
In recent years, there has been a surge of renewed interest in confidence distributions. In the more recent developments, the concept of confidence distribution has emerged as a purely frequentist
Frequentist inference
Frequentist inference is one of a number of possible ways of formulating generally applicable schemes for making statistical inferences: that is, for drawing conclusions from statistical samples. An alternative name is frequentist statistics...
concept, without any fiducial interpretation or reasoning. Conceptually, a confidence distribution is no different from a point estimator or an interval estimator (confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
), but it uses a sample-dependent distribution function on the parameter space (instead of a point or an interval) to estimate the parameter of interest.
A simple example of a confidence distribution, that has been broadly used in statistical practice, is a bootstrap
Bootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
distribution. The development and interpretation of a bootstrap distribution does not involve any fiducial reasoning; the same is true for the concept of a confidence distribution. But the notion of confidence distribution is much broader than that of a bootstrap distribution. In particular, recent research suggests that it encompasses and unifies a wide range of examples, from regular parametric cases (including most examples of the classical development of Fisher's fiducial distribution) to bootstrap distributions, p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
functions, normalized likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
s and, in some cases, Bayesian priors and Bayesian posteriors.
Just as a Bayesian posterior distribution contains a wealth of information for any type of Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, a confidence distribution contains a wealth of information for constructing almost all types of frequentist inferences, including point estimates, confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s and p-values, among others. Some recent developments have highlighted the promising potentials of the CD concept, as an effective inferential tool.
The history of CD concept
Neyman (1937) introduced the idea of "confidence" in his seminal paper on confidence intervals which clarified the frequentist repetition property. According to Fraser, the seed (idea) of confidence distribution can even be traced back to Bayes (1763) and Fisher (1930). Some researchers view the confidence distribution as "the Neymanian interpretation of Fishers fiducial distribution", which was "furiously disputed by Fisher". It is also believed that these "unproductive disputes" and Fisher's "stubborn insistence" might be the reason that the concept of confidence distribution has been long misconstrued as a fiducial concept and not been fully developed under the frequentist framework. Indeed, the confidence distribution is a purely frequentist concept with a purely frequentist interpretation, and it also has ties to Bayesian inference concepts and the fiducial arguments.Classical definition
Classically, a confidence distribution is defined by inverting the upper limits of a series of lower sided confidence intervals.. In particular,Definition (classical definition): For every α in (0, 1), let (−∞, ξn(α)] be a 100α% lower-side confidence side interval for θ, where ξn(α) = ξn(Xn,α) is continuous and increasing in α for each sample Xn. Then, Hn(•) = ξn−1(•) is a confidence distribution for θ.
Efron stated that this distribution "assigns probability 0.05 to θ lying between the upper endpoints of the 0.90 and 0.95 confidence interval, etc." and "it has powerful intuitive appeal".
In the classical literature, the confidence distribution function is interpreted as a distribution function of the parameter θ, which is impossible unless fiducial reasoning is involved since, in a frequentist setting, the parameters are fixed and nonrandom.
To interpret the CD function entirely from a frequentist viewpoint and not interpret it as a distribution function of a (fixed/nonrandom) parameter is one of the major departures of recent development relative to the classical approach. The nice thing about treating confidence distribution as a purely frequentist concept (similar to a point estimator) is that it is now free from those restrictive, if not controversial, constraints set forth by Fisher on fiducial distributions.
The modern definition
The following definition applies. In the definition, Θ is the parameter space of the unknown parameter of interest θ, and χ is the sample space corresponding to data Xn={X1,...,Xn}.Definition: A function Hn(•) = Hn(Xn, •) on χ × Θ → [0, 1] is called a confidence distribution (CD) for a parameter θ, if it follows two requirements:
- (R1) For each given Xn ∈ χ is a continuous cumulative distribution function on Θ;
- (R2) At the true parameter value θ = θ0, Hn(θ0) ≡ Hn(Xn, θ0), as a function of the sample Xn, follows the uniform distribution U[0, 1].
Also, the function H is an asymptotic CD (aCD), if the U[0, 1] requirement is true only asymptotically and the continuity requirement on Hn(•) is dropped.
In nontechnical terms, a confidence distribution is a function of both the parameter and the random sample, with two requirements. The first requirement (R1) simply requires that a CD should be a distribution on the parameter space. The second requirement (R2) sets a restriction on the function so that inferences (point estimators, confidence intervals and hypothesis testing, etc.) based on the confidence distribution have desired frequentist properties. This is similar to the restrictions in point estimation to ensure certain desired properties, such as unbiasedness, consistency, efficiency, etc.
A confidence distribution derived by inverting the upper limits of confidence intervals (classical definition) also satisfies the requirements in the above definition and this version of the definition is consistent with the classical definition.
Unlike the classical fiducial inference, more than one confidence distributions may be available
to estimate a parameter under any specific setting. Also, unlike the classical fiducial inference, optimality is not a part of requirement.
Depending on the setting and the criterion used, sometimes there is an
unique "best" (in terms of optimality) confidence distribution. But sometimes there is no optimal
confidence distribution available or, in some extreme cases, we may not even be able to find a meaningful confidence distribution. This is not different from the practice of point estimation.
Examples
Example 1: Normal Mean and VarianceSuppose a normal sample Xi ~ N(μ, σ2), i = 1, 2, ..., n is given.
(1) Variance σ2 is known
Both the functions
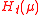and given by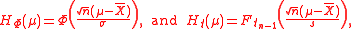satisfy the two requirements in the CD definition, and they are confidence distribution functions for μ. Here, Φ is the cumulative distribution function of the standard normal distribution, and
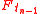is the cumulative distribution function of the student distribution. Furthermore,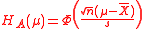satisfies the definition of an asymptotic confidence distribution when n→∞, and it is an asymptotic confidence distribution for μ. The uses of
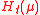and 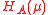are equivalent to state that we use 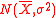and 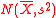to estimate , respectively.(2) Variance σ2 is unknown
For the parameter μ, since
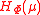involves the unknown parameter σ and it violates the two requirements in the CD definition, it is no longer a "distribution estimator" or a confidence distribution for μ. However, 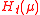is still a CD for μ and 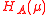is an aCD for μ.For the parameter σ2, the sample-dependent cumulative distribution function
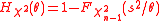
is a confidence distribution function for σ2. Here,
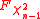is the cumulative distribution function of the student 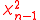distribution.In the case when the variance σ2 is known,
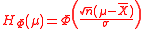is optimal in terms of producing the shortest confidence intervals at any given level. In the case when the variance σ2 is unknown, is an optimal confidence distribution for μ.Example 2: Bivariate normal correlation
Let ρ denotes the correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
of a bivariate normal population. It is well known that Fisher's z defined by the Fisher transformation
Fisher transformation
In statistics, hypotheses about the value of the population correlation coefficient ρ between variables X and Y can be tested using the Fisher transformation applied to the sample correlation coefficient r.-Definition:...
:
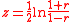
has the limiting distribution
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
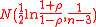with a fast rate of convergence, where r is the sample correlation and n is the sample size.The function
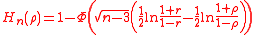
is an asymptotic confidence distribution for ρ.
Confidence interval
From the CD definition, it is evident that the interval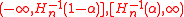 and 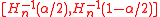provide 100(1 − α)%-level confidence intervals of different kinds, for θ, for any α ∈ (0, 1). Also 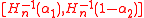is a level 100(1 − α1 − α2)% confidence interval for the parameter θ for any α1 > 0, α2 > 0 and α1 + α2 < 1. Here, 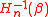is the 100β% quantile of 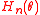or it solves for θ in equation 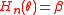. The same holds for an aCD, where the confidence level is achieved in limit.Point estimation
Point estimators can also be constructed given a confidence distribution estimator for the parameter of interest. For example, given Hn(θ) the CD for a parameter θ, natural choices of point estimators include the median Mn = Hn−1(1/2), the mean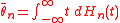, and the maximum point of the CD densityUnder some modest conditions, among other properties, one can prove that these point estimators are all consistent.
Hypothesis testing
One can derive a p-value for a test, either one-sided or two-sided, concerning the parameter θ, from its confidence distribution Hn(θ). Denote by the probability mass of a set C under the confidence distribution function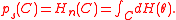 This ps(C) is called "support" in the CD inference and also known as "belief" in the fiducial literature. We have(1) For the one-sided test K0: θ ∈ C vs. K1: θ ∈ Cc, where C is of the type of (−∞, b] or [b, ∞), one can show from the CD definition that supθ ∈ CPθ(ps(C) ≤ α) = α. Thus, ps(C) = Hn(C) is the corresponding p-value of the test.
(2) For the singleton test K0: θ = b vs. K1: θ ≠ b, P{K0: θ = b}(2 min{ps(Clo), one can show from the CD definition that ps(Cup)} ≤ α) = α. Thus, 2 min{ps(Clo), ps(Cup)} = 2 min{Hn(b), 1 − Hn(b)} is the corresponding p-value of the test. Here, Clo = (−∞, b] and Cup = [b, ∞).
See Figure 1 from Xie and Singh (2011) for a graphical illustration of the CD inference.