
Compound probability distribution
Encyclopedia
In probability theory
, a compound probability distribution is the probability distribution
that results from assuming that a random variable
is distributed according to some parametrized distribution with an unknown parameter θ that is distributed according to some other distribution G, and then determining the distribution that results from marginalizing
with an unknown parameter θ that is distributed according to some other distribution G, and then determining the distribution that results from marginalizing
over G (i.e. integrating the unknown parameter out). The resulting distribution H is said to be the distribution that results from compounding F with G. In Bayesian inference
, the distribution G is often a conjugate prior
of F.
of the resulting compound distribution is the same as the support of the original distribution
is the same as the support of the original distribution  . For example, a beta-binomial distribution is discrete just as the binomial distribution is (however, its shape is similar to that of a beta distribution). The variance
. For example, a beta-binomial distribution is discrete just as the binomial distribution is (however, its shape is similar to that of a beta distribution). The variance
of the compound distribution is typically greater than the variance of the original distribution
is typically greater than the variance of the original distribution  . The parameters of
. The parameters of  include the parameters of
include the parameters of  and any parameters of
and any parameters of  that are not marginalized out. For example, the beta-binomial distribution includes three parameters, a parameter
that are not marginalized out. For example, the beta-binomial distribution includes three parameters, a parameter  (number of samples) from the binomial distribution and shape parameter
(number of samples) from the binomial distribution and shape parameter
s and
and 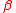 from the beta distribution.
from the beta distribution.
Note also that, in general, the probability density function
of the result of compounding an exponential family
distribution with its conjugate prior
distribution can be determined analytically. Assume that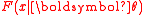 is a member of the exponential family with parameter
is a member of the exponential family with parameter 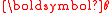 that is parametrized according to the natural parameter
that is parametrized according to the natural parameter  , and is distributed as
, and is distributed as

while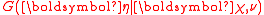 is the appropriate conjugate prior, distributed as
is the appropriate conjugate prior, distributed as
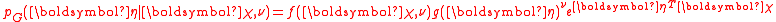
Then the result of compounding
of compounding  with
with  is
is
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a compound probability distribution is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
that results from assuming that a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is distributed according to some parametrized distribution
 with an unknown parameter θ that is distributed according to some other distribution G, and then determining the distribution that results from marginalizing
with an unknown parameter θ that is distributed according to some other distribution G, and then determining the distribution that results from marginalizingMarginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
over G (i.e. integrating the unknown parameter out). The resulting distribution H is said to be the distribution that results from compounding F with G. In Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, the distribution G is often a conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
of F.
Examples
- Compounding a Gaussian distribution with meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
distributed according to another Gaussian distribution yields a Gaussian distribution. - Compounding a Gaussian distribution with precisionPrecision (statistics)In statistics, the term precision can mean a quantity defined in a specific way. This is in addition to its more general meaning in the contexts of accuracy and precision and of precision and recall....
(reciprocal of varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
) distributed according to a gamma distribution yields a three-parameter Student's t distribution. - Compounding a binomial distribution with probability of success distributed according to a beta distribution yields a beta-binomial distribution.
- Compounding a multinomial distribution with probability vector distributed according to a Dirichlet distribution yields a multivariate Pólya distributionMultivariate Polya distributionThe multivariate Pólya distribution, named after George Pólya, also called the Dirichlet compound multinomial distribution, is a compound probability distribution, where a probability vector p is drawn from a Dirichlet distribution with parameter vector \alpha, and a set of discrete samples is...
, also known as a Dirichlet compound multinomial distribution. - Compounding a gamma distribution with inverse scale parameter distributed according to another gamma distribution yields a three-parameter beta prime distribution.
Theory
Note that the supportSupport (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of the resulting compound distribution
 is the same as the support of the original distribution
is the same as the support of the original distribution  . For example, a beta-binomial distribution is discrete just as the binomial distribution is (however, its shape is similar to that of a beta distribution). The variance
. For example, a beta-binomial distribution is discrete just as the binomial distribution is (however, its shape is similar to that of a beta distribution). The varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the compound distribution
 is typically greater than the variance of the original distribution
is typically greater than the variance of the original distribution  . The parameters of
. The parameters of  include the parameters of
include the parameters of  and any parameters of
and any parameters of  that are not marginalized out. For example, the beta-binomial distribution includes three parameters, a parameter
that are not marginalized out. For example, the beta-binomial distribution includes three parameters, a parameter  (number of samples) from the binomial distribution and shape parameter
(number of samples) from the binomial distribution and shape parameterShape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
s
 and
and 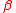 from the beta distribution.
from the beta distribution.Note also that, in general, the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the result of compounding an exponential family
Exponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
distribution with its conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
distribution can be determined analytically. Assume that
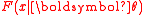 is a member of the exponential family with parameter
is a member of the exponential family with parameter 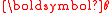 that is parametrized according to the natural parameter
that is parametrized according to the natural parameter  , and is distributed as
, and is distributed as
while
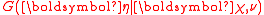 is the appropriate conjugate prior, distributed as
is the appropriate conjugate prior, distributed as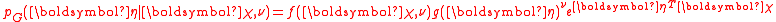
Then the result
 of compounding
of compounding  with
with  is
is-

The last line follows from the previous one by recognizing that the function inside the integral is the density function of a random variable distributed as , excluding the normalizingNormalizing constantThe concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
, excluding the normalizingNormalizing constantThe concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
function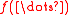 . Hence the result of the integration will be the reciprocal of the normalizing function.
. Hence the result of the integration will be the reciprocal of the normalizing function.
The above result is independent of choice of parametrization of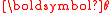 , as none of
, as none of  ,
, 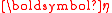 and
and  appears. (Note that
appears. (Note that  is a function of the parameter and hence will assume different forms depending on choice of parametrization.) For standard choices of
is a function of the parameter and hence will assume different forms depending on choice of parametrization.) For standard choices of  and
and  , it is often easier to work directly with the usual parameters rather than rewrite in terms of the natural parameters.
, it is often easier to work directly with the usual parameters rather than rewrite in terms of the natural parameters.
Note also that the reason the integral is tractable is that it involves computing the normalization constant of a density defined by the product of a prior distribution and a likelihoodLikelihoodLikelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
. When the two are conjugateConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
, the product is a posterior distribution, and by assumption, the normalization constant of this distribution is known. As shown above, the density function of the compound distribution follows a particular form, consisting of the product of the function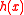 that forms part of the density function for
that forms part of the density function for  , with the quotient of two forms of the normalization "constant" for
, with the quotient of two forms of the normalization "constant" for  , one derived from a prior distribution and the other from a posterior distribution. The beta-binomial distribution is a good example of how this process works.
, one derived from a prior distribution and the other from a posterior distribution. The beta-binomial distribution is a good example of how this process works.
Despite the analytical tractability of such distributions, they are in themselves usually not members of the exponential familyExponential familyIn probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
. For example, the three-parameter Student's t distribution, beta-binomial distribution and Dirichlet compound multinomial distribution are not members of the exponential family. This can be seen above due to the presence of functional dependence on . In an exponential-family distribution, it must be possible to separate the entire density function into multiplicative factors of three types: (1) factors containing only variables, (2) factors containing only parameters, and (3) factors whose logarithm factorizes between variables and parameters. The presence of
. In an exponential-family distribution, it must be possible to separate the entire density function into multiplicative factors of three types: (1) factors containing only variables, (2) factors containing only parameters, and (3) factors whose logarithm factorizes between variables and parameters. The presence of 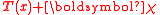 makes this impossible unless the "normalizing" function
makes this impossible unless the "normalizing" function  either ignores the corresponding argument entirely or uses it only in the exponent of an expression.
either ignores the corresponding argument entirely or uses it only in the exponent of an expression.
It is also possible to consider the result of compounding a joint distribution over a fixed number of independent identically distributed samples with a prior distribution over a shared parameter. When the distribution of the samples is from the exponential family and the prior distribution is conjugate, the resulting compound distribution will be tractable and follow a similar form to the expression above. It is easy to show, in fact, that the joint compound distribution of a set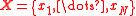 for
for  observations is
observations is

This result and the above result for a single compound distribution extend trivially to the case of a distribution over a vector-valued observation, such as a multivariate Gaussian distribution.
A related but slightly different concept of "compound" occurs with the compound Poisson distributionCompound Poisson distributionIn probability theory, a compound Poisson distribution is the probability distribution of the sum of a "Poisson-distributed number" of independent identically-distributed random variables...
. In one formulation of this, the compounding takes places over a distribution resulting from N underlying distributions, in which N is itself treated as a random variable. The compound Poisson distribution results from considering a set of independent identically-distributed random variables distributed according to J and asking what the distribution of their sum is, if the number of variables is itself an unknown random variable distributed according to a Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
distributed according to a Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
and independent of the variables being summed. In this case the random variable N is marginalized out much like θ above is marginalized out.

