In probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, the family of complex normal distributions consists of complex random variables whose real and imaginary parts are jointly normal. The complex normal family has three parameters: location parameter μ, covariance matrix Γ, and the relation matrix C. The standard complex normal is the univariate distribution with μ = 0, Γ = 1, and C = 0.

An important subclass of complex normal family is called the circular symmetric complex normal and corresponds to the case of zero relation matrix: C = 0. Circular symmetric complex normal random variables are used extensively in signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

, and are sometimes incorrectly referred to as just complex normal in signal processing literature.

Definition

Suppose X and Y are random vectors in R^k such that vec[X Y] is a 2k-dimensional normal random vector. Then we say that the complex random vector

has the complex normal distribution. This distribution can be described with 3 parameters:

where Z ′ denotes matrix transpose, and Z denotes complex conjugate

Complex conjugate

In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...

. Here the location parameter μ can be an arbitrary k-dimensional complex vector; the covariance matrix Γ must be Hermitian and non-negative definite; the relation matrix C should be symmetric. Moreover, matrices Γ and C are such that the matrix

is also non-negative definite.

Matrices Γ and C can be related to the covariance matrices of X and Y via expressions

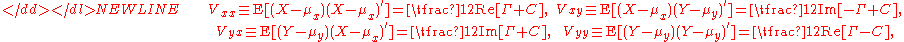
and conversely

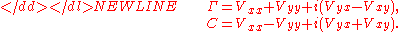
Density function

The probability density function for complex normal distribution can be computed as

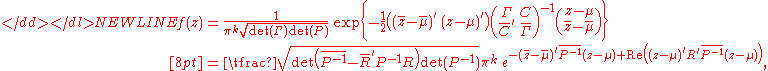
where R = C′ Γ ⁻¹ and P = Γ − RC.

Characteristic function

The characteristic function

Characteristic function (probability theory)

In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...

 of complex normal distribution is given by

where the argument w is a k-dimensional complex vector.

Properties

• If Z is a complex normal k-vector, A an ℓ×k matrix, and b a constant ℓ-vector, then the linear transform will be distributed also complex-normally:

• If Z is a complex normal k-vector, then

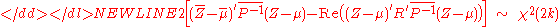
• Central limit theorem. If z₁, …, z_T are independent and identically distributed complex random variables, then

where Γ = E[ zz′ ] and C = E[ zz′ ].

Circular symmetric complex normal distribution

The circular symmetric complex normal distribution corresponds to the case of zero relation matrix, C=0. If is circular complex normal, then the vector vec[X Y] is multivariate normal with covariance structure

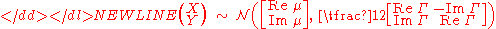
where and . This is usually denoted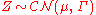
and its distribution can also be simplified as

The standard complex normal corresponds to the distribution of a scalar random variable with μ = 0, C = 0 and Γ = 1. Thus, the standard complex normal distribution has density

This expression demonstrates why the case C = 0 is called “circular-symmetric”. The density function depends only on the magnitude of z but not on its argument

Arg (mathematics)

In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...

. As such, the magnitude |z| of standard complex normal random variable will have the Rayleigh distribution and the squared magnitude |z|² will have the Exponential distribution

Exponential distribution

In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...

, whereas the argument will be distributed uniformly

Uniform distribution (continuous)

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...

 on [−π, π].

If {z₁, …, z_n} are independent and identically distributed k-dimensional circular complex normal random variables with μ = 0, then random squared norm

has the Generalized chi-squared distribution and the random matrix

has the complex Wishart distribution with n degrees of freedom. This distribution can be described by density function

where n ≥ k, and w is a k×k nonnegative-definite matrix.

See also

• Normal distribution
• Multivariate normal distribution
• Generalized chi-squared distribution
• Wishart distribution

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.