
Color-coding
Encyclopedia
In computer science
and graph theory
, the method of color-coding efficiently finds k-vertex simple paths
, k-vertex cycles
, and other small subgraphs within a given graph
using probabilistic algorithms, which can then be derandomized and turned into deterministic algorithm
s. This method shows that many subcases of the subgraph isomorphism problem (an NP-complete
problem) can in fact be solved in polynomial time.
The theory and analysis of the color-coding method was proposed in 1994 by Noga Alon
, Raphael Yuster, and Uri Zwick.
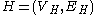 in a given graph
in a given graph 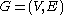 , where
, where  can be a path, a cycle, or any bounded treewidth graph where
can be a path, a cycle, or any bounded treewidth graph where 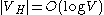 , the method of color-coding begins by randomly coloring each vertex of
, the method of color-coding begins by randomly coloring each vertex of 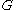 with
with 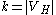 colors, and then tries to find a colorful copy of
colors, and then tries to find a colorful copy of 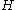 in colored
in colored 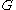 . Here, a graph is colorful if every vertex in it is colored with a distinct color. This method works by repeating (1) random coloring a graph and (2) finding colorful copy of the target subgraph, and eventually the target subgraph can be found if the process is repeated a sufficient number of times.
. Here, a graph is colorful if every vertex in it is colored with a distinct color. This method works by repeating (1) random coloring a graph and (2) finding colorful copy of the target subgraph, and eventually the target subgraph can be found if the process is repeated a sufficient number of times.
Suppose becomes colorful with some non-zero probability
becomes colorful with some non-zero probability 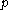 . It immediately follows that if the random coloring is repeated
. It immediately follows that if the random coloring is repeated 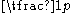 times, then
times, then 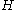 is expected to become colorful once. Note that though
is expected to become colorful once. Note that though 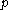 is small, it is shown that if
is small, it is shown that if  ,
,  is only polynomially small. Suppose again there exists an algorithm such that, given a graph
is only polynomially small. Suppose again there exists an algorithm such that, given a graph 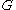 and a coloring which maps each vertex of
and a coloring which maps each vertex of  to one of the
to one of the  colors, it finds a copy of colorful
colors, it finds a copy of colorful 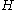 , if one exists, within some runtime
, if one exists, within some runtime 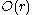 . Then the expected time to find a copy of
. Then the expected time to find a copy of  in
in 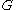 , if one exists, is
, if one exists, is  .
.
Sometimes it is also desirable to use a more restricted version of colorfulness. For example, in the context of finding cycles in planar graphs, it is possible to develop an algorithm that finds well-colored cycles. Here, a cycle is well-colored if its vertices are colored by consecutive colors.
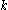 in graph
in graph 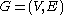 .
.
By applying random coloring method, each simple cycle has a probability of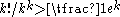 to become colorful, since there are
to become colorful, since there are 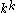 ways of coloring the
ways of coloring the 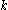 vertices on the path, among which there are
vertices on the path, among which there are 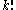 colorful occurrences. Then an algorithm (described below) of runtime
colorful occurrences. Then an algorithm (described below) of runtime  can be adopted to find colorful cycles in the randomly colored graph
can be adopted to find colorful cycles in the randomly colored graph 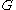 . Therefore, it takes
. Therefore, it takes 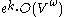 overall time to find a simple cycle of length
overall time to find a simple cycle of length 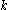 in
in 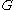 .
.
The colorful cycle-finding algorithm works by first finding all pairs of vertices in V that are connected by a simple path of length k − 1, and then checking whether the two vertices in each pair are connected. Given a coloring function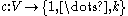 to color graph
to color graph 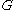 , enumerate all partitions of the color set
, enumerate all partitions of the color set 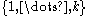 into two subsets
into two subsets  ,
, 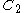 of size
of size 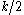 each. Note that
each. Note that 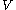 can be divided into
can be divided into  and
and 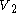 accordingly, and let
accordingly, and let 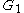 and
and 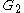 denote the subgraphs induced by
denote the subgraphs induced by  and
and  respectively. Then, recursively finds colorful path of length
respectively. Then, recursively finds colorful path of length 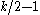 in each of
in each of 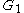 and
and 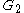 . Suppose the boolean matrix
. Suppose the boolean matrix  and
and 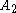 represent the connectivity of each pair of vertices in
represent the connectivity of each pair of vertices in 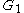 and
and  by a colorful path, respectively, and let
by a colorful path, respectively, and let 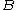 be the matrix describing the adjacency relations between vertices of
be the matrix describing the adjacency relations between vertices of 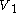 and those of
and those of 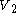 , the boolean product
, the boolean product 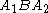 gives all pairs of vertices in
gives all pairs of vertices in 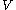 that are connected by a colorful path of length
that are connected by a colorful path of length 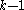 . Thus, the recursive relation of matrix multiplications is
. Thus, the recursive relation of matrix multiplications is  , which yields a runtime of
, which yields a runtime of 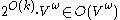 . Although this algorithm finds only the end points of the colorful path, another algorithm by Alon and Naor that finds colorful paths themselves can be incorporated into it.
. Although this algorithm finds only the end points of the colorful path, another algorithm by Alon and Naor that finds colorful paths themselves can be incorporated into it.
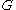 , such that the randomness of coloring
, such that the randomness of coloring 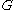 is no longer required. For the target subgraph
is no longer required. For the target subgraph 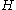 in
in 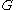 to be discoverable, the enumeration has to include at least one instance where the
to be discoverable, the enumeration has to include at least one instance where the 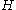 is colorful. To achieve this, enumerating a
is colorful. To achieve this, enumerating a 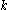 -perfect family
-perfect family 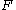 of hash functions from
of hash functions from  to
to  is sufficient. By definition,
is sufficient. By definition, 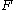 is k-perfect if for every subset
is k-perfect if for every subset 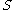 of
of 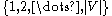 where
where 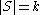 , there exists a hash function
, there exists a hash function 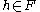 such that
such that  is perfect. In other words, there must exist a hash function in
is perfect. In other words, there must exist a hash function in 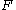 that colors any given
that colors any given 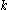 vertices with
vertices with 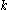 distinct colors.
distinct colors.
There are several approaches to construct such a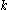 -perfect hash family:
-perfect hash family:
In the case of derandomizing well-coloring, where each vertex on the subgraph is colored consecutively, a -perfect family of hash functions from
-perfect family of hash functions from 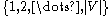 to
to 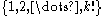 is needed. A sufficient
is needed. A sufficient 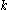 -perfect family which maps from
-perfect family which maps from 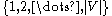 to
to  can be constructed in a way similar to the approach 3 above (the first step). In particular, it is done by using
can be constructed in a way similar to the approach 3 above (the first step). In particular, it is done by using 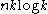 random bits that are almost
random bits that are almost 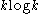 independent, and the size of the resulting
independent, and the size of the resulting 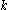 -perfect family will be
-perfect family will be 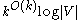 .
.
The derandomization of color-coding method can be easily parallelized, yielding efficient NC
algorithms.
in protein-protein interaction
(PPI) networks. Another example is to discover and to count the number of motifs
in PPI networks. Studying both signaling pathways
and motifs
allows a deeper understanding of the similarities and differences of many biological functions, processes, and structures among organisms.
Due to the huge amount of gene data that can be collected, searching for pathways or motifs can be highly time consuming. However, by exploiting the color coding method, the motifs or signaling pathways with vertices in a network
vertices in a network 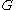 with
with  vertices can be found very efficiently in polynomial time. Thus, this enables us to explore more complex or larger structures in PPI networks. More details can be found in .
vertices can be found very efficiently in polynomial time. Thus, this enables us to explore more complex or larger structures in PPI networks. More details can be found in .
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the method of color-coding efficiently finds k-vertex simple paths
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
, k-vertex cycles
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
, and other small subgraphs within a given graph
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
using probabilistic algorithms, which can then be derandomized and turned into deterministic algorithm
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
s. This method shows that many subcases of the subgraph isomorphism problem (an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem) can in fact be solved in polynomial time.
The theory and analysis of the color-coding method was proposed in 1994 by Noga Alon
Noga Alon
Noga Alon is an Israeli mathematician noted for his contributions to combinatorics and theoretical computer science, having authored hundreds of papers.- Academic background :...
, Raphael Yuster, and Uri Zwick.
Results
The following results can be obtained through the method of color-coding:- For every fixed constant
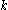 , if a graph
, if a graph 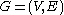 contains a simple cycle of size
contains a simple cycle of size 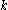 , then such cycle can be found in:
, then such cycle can be found in:
- O(
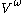 ) expected time, or
) expected time, or - O(
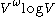 ) worst-case time, where
) worst-case time, where  is the exponent of matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
is the exponent of matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
.
- O(
- For every fixed constant
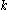 , and every graph
, and every graph 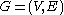 that is in any nontrivial minor-closed graph family (e.g., a planar graphPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
that is in any nontrivial minor-closed graph family (e.g., a planar graphPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
), if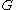 contains a simple cycle of size
contains a simple cycle of size  , then such cycle can be found in:
, then such cycle can be found in:
- O(
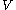 ) expected time, or
) expected time, or - O(
 ) worst-case time.
) worst-case time.
- O(
- If a graph
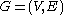 contains a subgraph isomorphic to a bounded treewidth graph which has
contains a subgraph isomorphic to a bounded treewidth graph which has 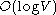 vertices, then such a subgraph can be found in polynomial time.
vertices, then such a subgraph can be found in polynomial time.
The method
To solve the problem of finding a subgraph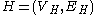 in a given graph
in a given graph 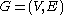 , where
, where  can be a path, a cycle, or any bounded treewidth graph where
can be a path, a cycle, or any bounded treewidth graph where 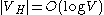 , the method of color-coding begins by randomly coloring each vertex of
, the method of color-coding begins by randomly coloring each vertex of 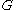 with
with 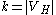 colors, and then tries to find a colorful copy of
colors, and then tries to find a colorful copy of 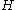 in colored
in colored 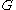 . Here, a graph is colorful if every vertex in it is colored with a distinct color. This method works by repeating (1) random coloring a graph and (2) finding colorful copy of the target subgraph, and eventually the target subgraph can be found if the process is repeated a sufficient number of times.
. Here, a graph is colorful if every vertex in it is colored with a distinct color. This method works by repeating (1) random coloring a graph and (2) finding colorful copy of the target subgraph, and eventually the target subgraph can be found if the process is repeated a sufficient number of times.Suppose
 becomes colorful with some non-zero probability
becomes colorful with some non-zero probability 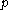 . It immediately follows that if the random coloring is repeated
. It immediately follows that if the random coloring is repeated 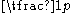 times, then
times, then 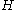 is expected to become colorful once. Note that though
is expected to become colorful once. Note that though 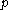 is small, it is shown that if
is small, it is shown that if  ,
,  is only polynomially small. Suppose again there exists an algorithm such that, given a graph
is only polynomially small. Suppose again there exists an algorithm such that, given a graph 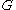 and a coloring which maps each vertex of
and a coloring which maps each vertex of  to one of the
to one of the  colors, it finds a copy of colorful
colors, it finds a copy of colorful 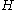 , if one exists, within some runtime
, if one exists, within some runtime 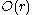 . Then the expected time to find a copy of
. Then the expected time to find a copy of  in
in 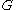 , if one exists, is
, if one exists, is  .
.Sometimes it is also desirable to use a more restricted version of colorfulness. For example, in the context of finding cycles in planar graphs, it is possible to develop an algorithm that finds well-colored cycles. Here, a cycle is well-colored if its vertices are colored by consecutive colors.
Example
An example would be finding a simple cycle of length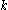 in graph
in graph 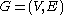 .
.By applying random coloring method, each simple cycle has a probability of
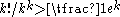 to become colorful, since there are
to become colorful, since there are 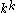 ways of coloring the
ways of coloring the 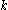 vertices on the path, among which there are
vertices on the path, among which there are 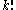 colorful occurrences. Then an algorithm (described below) of runtime
colorful occurrences. Then an algorithm (described below) of runtime  can be adopted to find colorful cycles in the randomly colored graph
can be adopted to find colorful cycles in the randomly colored graph 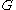 . Therefore, it takes
. Therefore, it takes 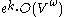 overall time to find a simple cycle of length
overall time to find a simple cycle of length 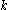 in
in 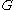 .
.The colorful cycle-finding algorithm works by first finding all pairs of vertices in V that are connected by a simple path of length k − 1, and then checking whether the two vertices in each pair are connected. Given a coloring function
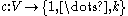 to color graph
to color graph 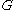 , enumerate all partitions of the color set
, enumerate all partitions of the color set 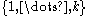 into two subsets
into two subsets  ,
, 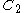 of size
of size 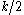 each. Note that
each. Note that 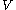 can be divided into
can be divided into  and
and 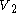 accordingly, and let
accordingly, and let 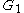 and
and 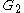 denote the subgraphs induced by
denote the subgraphs induced by  and
and  respectively. Then, recursively finds colorful path of length
respectively. Then, recursively finds colorful path of length 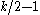 in each of
in each of 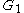 and
and 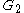 . Suppose the boolean matrix
. Suppose the boolean matrix  and
and 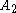 represent the connectivity of each pair of vertices in
represent the connectivity of each pair of vertices in 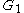 and
and  by a colorful path, respectively, and let
by a colorful path, respectively, and let 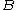 be the matrix describing the adjacency relations between vertices of
be the matrix describing the adjacency relations between vertices of 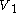 and those of
and those of 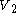 , the boolean product
, the boolean product 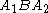 gives all pairs of vertices in
gives all pairs of vertices in 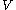 that are connected by a colorful path of length
that are connected by a colorful path of length 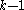 . Thus, the recursive relation of matrix multiplications is
. Thus, the recursive relation of matrix multiplications is  , which yields a runtime of
, which yields a runtime of 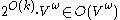 . Although this algorithm finds only the end points of the colorful path, another algorithm by Alon and Naor that finds colorful paths themselves can be incorporated into it.
. Although this algorithm finds only the end points of the colorful path, another algorithm by Alon and Naor that finds colorful paths themselves can be incorporated into it.Derandomization
The derandomization of color-coding involves enumerating possible colorings of a graph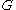 , such that the randomness of coloring
, such that the randomness of coloring 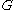 is no longer required. For the target subgraph
is no longer required. For the target subgraph 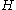 in
in 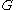 to be discoverable, the enumeration has to include at least one instance where the
to be discoverable, the enumeration has to include at least one instance where the 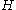 is colorful. To achieve this, enumerating a
is colorful. To achieve this, enumerating a 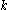 -perfect family
-perfect family 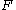 of hash functions from
of hash functions from  to
to  is sufficient. By definition,
is sufficient. By definition, 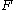 is k-perfect if for every subset
is k-perfect if for every subset 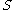 of
of 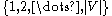 where
where 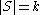 , there exists a hash function
, there exists a hash function 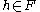 such that
such that  is perfect. In other words, there must exist a hash function in
is perfect. In other words, there must exist a hash function in 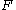 that colors any given
that colors any given 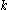 vertices with
vertices with 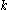 distinct colors.
distinct colors.There are several approaches to construct such a
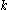 -perfect hash family:
-perfect hash family:- The best explicit construction is by Moni NaorMoni NaorMoni Naor is an Israeli computer scientist, currently a professor at the Weizmann Institute of Science. Naor received his Ph.D. in 1989 at the University of California, Berkeley. His adviser was Manuel Blum....
, Leonard J. Schulman, and Aravind Srinivasan, where a family of size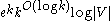 can be obtained. This construction does not require the target subgraph to exist in the original subgraph finding problem.
can be obtained. This construction does not require the target subgraph to exist in the original subgraph finding problem. - Another explicit construction by Jeanette P. Schmidt and Alan SiegelAlan SiegelAlan Siegel is founder and Chairman of Siegel+Gale.-Early life:Alan Siegel was born August 26, 1938 to Eugene and Ruth Siegel in New York. Siegel attended Long Beach High where he played basketball under Robert Gersten. His dream was always to go to college on a basketball scholarship...
yields a family of size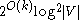 .
. - Another construction that appears in the original paper of Noga AlonNoga AlonNoga Alon is an Israeli mathematician noted for his contributions to combinatorics and theoretical computer science, having authored hundreds of papers.- Academic background :...
et al. can be obtained by first building a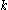 -perfect family that maps
-perfect family that maps 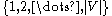 to
to 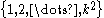 , followed by building another
, followed by building another  -perfect family that maps
-perfect family that maps 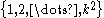 to
to 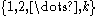 . In the first step, it is possible to construct such a family with
. In the first step, it is possible to construct such a family with 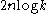 random bits that are almost
random bits that are almost 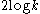 -wise independent, and the sample space needed for generating those random bits can be as small as
-wise independent, and the sample space needed for generating those random bits can be as small as 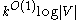 . In the second step, it has been shown by Jeanette P. Schmidt and Alan Siegel that the size of such
. In the second step, it has been shown by Jeanette P. Schmidt and Alan Siegel that the size of such 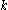 -perfect family can be
-perfect family can be 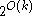 . Consequently, by composing the
. Consequently, by composing the 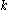 -perfect families from both steps, a
-perfect families from both steps, a 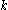 -perfect family of size
-perfect family of size  that maps from
that maps from  to
to 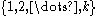 can be obtained.
can be obtained.
In the case of derandomizing well-coloring, where each vertex on the subgraph is colored consecutively, a
 -perfect family of hash functions from
-perfect family of hash functions from 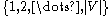 to
to 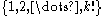 is needed. A sufficient
is needed. A sufficient 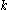 -perfect family which maps from
-perfect family which maps from 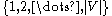 to
to  can be constructed in a way similar to the approach 3 above (the first step). In particular, it is done by using
can be constructed in a way similar to the approach 3 above (the first step). In particular, it is done by using 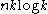 random bits that are almost
random bits that are almost 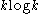 independent, and the size of the resulting
independent, and the size of the resulting 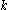 -perfect family will be
-perfect family will be 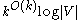 .
.The derandomization of color-coding method can be easily parallelized, yielding efficient NC
NC (complexity)
In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
algorithms.
Applications
Recently, color coding has attracted much attention in the field of bioinformatics. One example is the detection of signaling pathwaysWnt signaling pathway
The Wnt signaling pathway is a network of proteins best known for their roles in embryogenesis and cancer, but also involved in normal physiological processes in adult animals.-Discovery:...
in protein-protein interaction
Protein-protein interaction
Protein–protein interactions occur when two or more proteins bind together, often to carry out their biological function. Many of the most important molecular processes in the cell such as DNA replication are carried out by large molecular machines that are built from a large number of protein...
(PPI) networks. Another example is to discover and to count the number of motifs
Structural motif
In a chain-like biological molecule, such as a protein or nucleic acid, a structural motif is a supersecondary structure, which appears also in a variety of other molecules...
in PPI networks. Studying both signaling pathways
Wnt signaling pathway
The Wnt signaling pathway is a network of proteins best known for their roles in embryogenesis and cancer, but also involved in normal physiological processes in adult animals.-Discovery:...
and motifs
Structural motif
In a chain-like biological molecule, such as a protein or nucleic acid, a structural motif is a supersecondary structure, which appears also in a variety of other molecules...
allows a deeper understanding of the similarities and differences of many biological functions, processes, and structures among organisms.
Due to the huge amount of gene data that can be collected, searching for pathways or motifs can be highly time consuming. However, by exploiting the color coding method, the motifs or signaling pathways with
 vertices in a network
vertices in a network 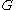 with
with  vertices can be found very efficiently in polynomial time. Thus, this enables us to explore more complex or larger structures in PPI networks. More details can be found in .
vertices can be found very efficiently in polynomial time. Thus, this enables us to explore more complex or larger structures in PPI networks. More details can be found in .

