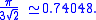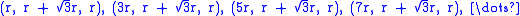Close-packing
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, close-packing of equal sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
). Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a regular lattice arrangement is
The same packing density can also be achieved by alternate stackings of the same close-packed planes of spheres, including structures that are aperiodic in the stacking direction. The Kepler conjecture
Kepler conjecture
The Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
states that this is the highest density that can be achieved by any arrangement of spheres, either regular or irregular. This conjecture is now widely considered proven by T. C. Hales
Thomas Callister Hales
Thomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...
.
Many crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
structures are based on a close-packing of atoms, or of large ions with smaller ions filling the spaces between them. The cubic and hexagonal arrangements are very close to one another in energy, and it may be difficult to predict which form will be preferred from first principles.
fcc and hcp lattices
There are two simple regular lattices that achieve this highest average density. They are called face-centered cubic (fcc) (also called cubicCubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
close packed) and hexagonal close-packed (hcp), based on their symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. Both are based upon sheets of spheres arranged at the vertices of a triangular tiling; they differ in how the sheets are stacked upon one another.
Cannonball problem
The problem of close-packing of spheres was first mathematically analyzed by Thomas HarriotThomas Harriot
Thomas Harriot was an English astronomer, mathematician, ethnographer, and translator. Some sources give his surname as Harriott or Hariot or Heriot. He is sometimes credited with the introduction of the potato to Great Britain and Ireland...
around 1587, after a question on piling cannonballs on ships was posed to him by Sir Walter Raleigh
Walter Raleigh
Sir Walter Raleigh was an English aristocrat, writer, poet, soldier, courtier, spy, and explorer. He is also well known for popularising tobacco in England....
on their expedition to America. Cannonballs were usually piled in a rectangular or triangular wooden frame, forming a three-sided or four-sided pyramid. Both arrangements produce a face-centered cubic lattice – with different orientation to the ground.
Positioning and spacing
In both the fcc and hcp arrangements each sphere has twelve neighbors. For every sphere there is one gap surrounded by six spheres (octahedral) and two smaller gaps surrounded by four spheres (tetrahedral). The distances to the centers of these gaps from the centers of the surrounding spheres is
for the tetrahedral, and 
for the octahedral, when the sphere radius is 1.Relative to a reference layer with positioning A, two more positionings B and C are possible. Every sequence of A, B, and C without immediate repetition of the same one is possible and gives an equally dense packing for spheres of a given radius.
The most regular ones are:
- fcc = ABCABCA (every third layer is the same)
- hcp = ABABABA (every other layer is the same)
In close-packing, the center-to-center spacing of spheres in the x–y plane is a simple honeycomb-like tessellation with a pitch (distance between sphere centers) of one sphere diameter. The distance between sphere centers, projected on the z (vertical) axis, is:
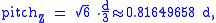
where d is the diameter of a sphere; this follows from the tetrahedral arrangement of close-packed spheres.
The coordination number
Coordination number
In chemistry and crystallography, the coordination number of a central atom in a molecule or crystal is the number of its nearest neighbours. This number is determined somewhat differently for molecules and for crystals....
of hcp and fcc is 12 and its atomic packing factor
Atomic packing factor
In crystallography, atomic packing factor or packing fraction is the fraction of volume in a crystal structure that is occupied by atoms. It is dimensionless and always less than unity. For practical purposes, the APF of a crystal structure is determined by assuming that atoms are rigid spheres...
(APF) is the number mentioned above, 0.74.
| Comparison between hcp and fcc | ||
|---|---|---|
 |
 |
|
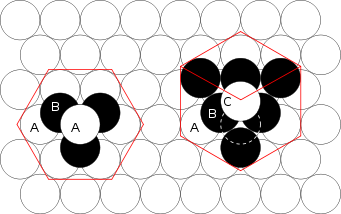
| Figure 1 – The hcp lattice (left) and the fcc lattice (right). The outline of each respective Bravais lattice is shown in red. The letters indicate which layers are the same. There are two "A" layers in the hcp matrix, where all the spheres are in the same position. All three layers in the fcc stack are different. Note the fcc stacking may be converted to the hcp stacking by translation of the upper-most sphere, as shown by the dashed outline. | Figure 2 – Thomas Harriot Thomas Harriot Thomas Harriot was an English astronomer, mathematician, ethnographer, and translator. Some sources give his surname as Harriott or Hariot or Heriot. He is sometimes credited with the introduction of the potato to Great Britain and Ireland... , circa 1585, first pondered the mathematics of the cannonball arrangement or cannonball stack, which has an fcc lattice. Note how adjacent balls along each edge of the regular tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... enclosing the stack are all in direct contact with one another. This does not occur in an hcp lattice, as shown in Fig. 3. |
Figure 3 – Shown here is a stack of eleven spheres of the hcp lattice illustrated in Fig. 1. The hcp stack differs from the top 3 tiers of the fcc stack shown in Fig. 2 only in the lowest tier; it can be modified to fcc by an appropriate rotation or translation. |
Lattice generation
When forming any sphere-packing lattice, the first fact to notice is that whenever two spheres touch a straight line may be drawn from the center of one sphere to the center of the other intersecting the point of contact. The distance between the centers along the shortest path namely that straight line will therefore be r1 + r2 where r1 is the radius of the first sphere and r2 is the radius of the second. In close packing all of the spheres share a common radius, r. Therefore two centers would simply have a distance 2r.Simple hcp lattice
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
.
First form a row of spheres. The centers will all lie on a straight line. Their x-coordinate will vary by 2r since the distance between each center if the spheres are touching is 2r. The y-coordinate and z-coordinate will be the same. For simplicity, say that the balls are the first row and that their y- and z-coordinates are simply r, so that their surfaces rest on the zero-planes. Coordinates of the centers of the first row will look like (2r, r, r), (4r, r, r), (6r ,r, r), (8r ,r, r), ... . The sphere centered at x = 0 is immediately omitted because part of the sphere would lie outside.
Now, form the next row of spheres. Again, the centers will all lie on a straight line with x-coordinate differences of 2r, but there will be a shift of distance r in the x-direction so that the center of every sphere in this row aligns with the x-coordinate of where two spheres touch in the first row. This allows the spheres of the new row to slide in closer to the first row until all spheres in the new row are touching two spheres of the first row. Since the new spheres touch two spheres, their centers form an equilateral triangle with those two neighbors' centers. The side lengths are all 2r, so the height or y-coordinate difference between the rows is
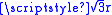. Thus, this row will have coordinates like this:
The first sphere of this row only touches one sphere in the original row, but its location follows suit with the rest of the row.
The next row follows this pattern of shifting the x-coordinate by r and the y-coordinate by
. Add rows until reaching the x and y maximum borders of the box.In an A-B-A-B-... stacking pattern, the odd numbered planes of spheres will have exactly the same coordinates save for a pitch difference in the z-coordinates and the even numbered planes of spheres will share the same x- and y-coordinates. Both types of planes are formed using the pattern mentioned above, but the starting place for the first row's first sphere will be different.
Using the plane described precisely above as plane #1, the A plane, place a sphere on top of this plane so that it lies touching three spheres in the A-plane. The three spheres are all already touching each other, forming an equilateral triangle, and since they all touch the new sphere, the four centers form a regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. All of the sides are equal to 2r because all of the sides are formed by two spheres touching. The height of which or the z-coordinate difference between the two "planes" is
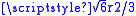. This, combined with the offsets in the x and y-coordinates gives the centers of the first row in the B plane:
The second row's coordinates follow the pattern first described above and are:
The difference to the next plane, the A plane, is again
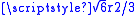in the z-direction and a shift in the x and y to match those x- and y-coordinates of the first A plane.Miller indices
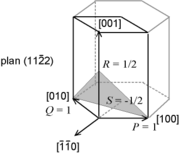
Miller index
Miller indices form a notation system in crystallography for planes and directions in crystal lattices.In particular, a family of lattice planes is determined by three integers h, k, and ℓ, the Miller indices. They are written , and each index denotes a plane orthogonal to a direction in the...
notation ( hkil ) in which the third index i denotes a convenient but degenerate component which is equal to −h − k. The h, i and k index directions are separated by 120°, and are thus not orthogonal; the l component is mutually perpendicular to the h, i and k index directions.
See also
- Sphere packingSphere packingIn geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
- Cubic crystal systemCubic crystal systemIn crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
- Honeycomb (geometry)Honeycomb (geometry)In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
- Hermite constant