Miller index
Encyclopedia
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
for planes and directions in crystal (Bravais) lattices.
In particular, a family of lattice plane
Lattice plane
In crystallography, a lattice plane of a given Bravais lattice is a plane whose intersections with the lattice are periodic and intersect the Bravais lattice; equivalently, a lattice plane is any plane containing at least three noncollinear Bravais lattice points...
s is determined by three integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s h, k, and ℓ, the Miller indices. They are written (hkℓ), and each index denotes a plane orthogonal to a direction (h, k, ℓ) in the basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
vectors. By convention, negative integers are written with a bar, as in for −3. The integers are usually written in lowest terms, i.e. their greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
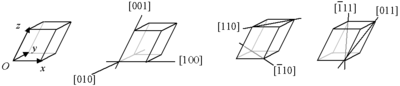
should be 1. Miller index 100 represents a plane orthogonal to direction h; index 010 represents a plane orthogonal to direction k, and index 001 represents a plane orthogonal to ℓ.
There are also several related notations:
- the notation {hkℓ} denotes the set of all planes that are equivalent to (hkℓ) by the symmetry of the lattice.
In the context of crystal directions (not planes), the corresponding notations are:
- [hkℓ], with square instead of round brackets, denotes a direction in the basis of the direct lattice vectors instead of the reciprocal lattice; and
- similarly, the notation 〈hkℓ〉 denotes the set of all directions that are equivalent to [hkℓ] by symmetry.
Miller indices were introduced in 1839 by the British mineralogist William Hallowes Miller
William Hallowes Miller
William Hallowes Miller FRS , British mineralogist and crystallographer.- Life and work :Miller was born in 1801 at Velindre near Llandovery, Carmarthenshire. He was educated at St John's College, Cambridge, where he graduated in 1826 as fifth wrangler. He became a Fellow there in 1829...
. The method was also historically known as the Millerian system, and the indices as Millerian, although this is now rare.
The precise meaning of this notation depends upon a choice of lattice vectors for the crystal, as described below. Usually, three primitive lattice vectors are used. However, for cubic crystal systems, the cubic lattice vectors are used even when they are not primitive (e.g., as in body-centered and face-centered crystals).
Definition
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
, or as the inverse intercepts along the lattice vectors. Both definitions are given below. In either case, one needs to choose the three lattice vectors a1, a2, and a3 that define the unit cell (note that the conventional unit cell may be larger than the primitive cell of the Bravais lattice, as the examples below illustrate). Given these, the three primitive reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
vectors are also determined (denoted b1, b2, and b3).
Then, given the three Miller indices h, k, ℓ, (hkℓ) denotes planes orthogonal to the reciprocal lattice vector:
That is, (hkℓ) simply indicates a normal to the planes in the basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the primitive reciprocal lattice vectors. Because the coordinates are integers, this normal is itself always a reciprocal lattice vector. The requirement of lowest terms means that it is the shortest reciprocal lattice vector in the given direction.
Equivalently, (hkℓ) denotes a plane that intercepts the three points a1/h, a2/k, and a3/ℓ, or some multiple thereof. That is, the Miller indices are proportional to the inverses of the intercepts of the plane, in the basis of the lattice vectors. If one of the indices is zero, it means that the planes do not intersect that axis (the intercept is "at infinity").
Considering only (hkℓ) planes intersecting one or more lattice points (the lattice planes), the perpendicular distance d between adjacent lattice planes is related to the (shortest) reciprocal lattice vector orthogonal to the planes by the formula:
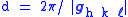.The related notation [hkℓ] denotes the direction:
That is, it uses the direct lattice basis instead of the reciprocal lattice. Note that [hkℓ] is not generally normal to the (hkℓ) planes, except in a cubic lattice as described below.
Case of cubic structures
For the special case of simple cubic crystals, the lattice vectors are orthogonal and of equal length (usually denoted a); similar to the reciprocal lattice. Thus, in this common case, the Miller indices (hkℓ) and [hkℓ] both simply denote normals/directions in Cartesian coordinates.For cubic crystals with lattice constant
Lattice constant
The lattice constant [or lattice parameter] refers to the constant distance between unit cells in a crystal lattice. Lattices in three dimensions generally have three lattice constants, referred to as a, b, and c. However, in the special case of cubic crystal structures, all of the constants are...
a, the spacing d between adjacent (hkℓ) lattice planes is (from above):
-
.
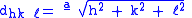Because of the symmetry of cubic crystals, it is possible to change the place and sign of the integers and have equivalent directions and planes:
- Coordinates in angle brackets such as 〈100〉 denote a family of directions which are equivalent due to symmetry operations, such as [100], [010], [001] or the negative of any of those directions.
- Coordinates in curly brackets or braces such as {100} denote a family of plane normals which are equivalent due to symmetry operations, much the way angle brackets denote a family of directions.
For face-centered cubic and body-centered cubic lattices, the primitive lattice vectors are not orthogonal. However, in these cases the Miller indices are conventionally defined relative to the lattice vectors of the cubic supercell
Supercell (crystal)
In solid-state physics and crystallography, when describing crystal structure, a supercell is a repeating unit cell of the crystal that contains several primitive cells...
and hence are again simply the Cartesian directions.
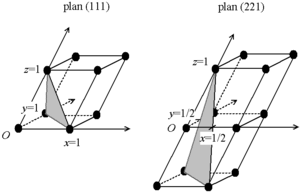
Case of hexagonal and rhombohedral structures
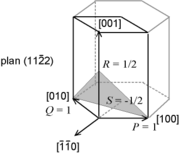
- i = −(h + k).
Here h, k and l are identical to the Miller index, and i is a redundant index.
This four-index scheme for labeling planes in a hexagonal lattice makes permutation symmetries apparent. For example, the similarity between (110) ≡ (110) and (10) ≡ (110) is more obvious when the redundant index is shown.
In the figure at right, the (001) plane has a 3-fold symmetry: it remains unchanged by a rotation of 1/3 (2π/3 rad, 120°). The [100], [010] and the [0] directions are really similar. If S is the intercept of the plane with the [0] axis, then
- i = 1/S.
There are also ad hoc
Ad hoc
Ad hoc is a Latin phrase meaning "for this". It generally signifies a solution designed for a specific problem or task, non-generalizable, and not intended to be able to be adapted to other purposes. Compare A priori....
schemes (e.g. in the transmission electron microscopy
Transmission electron microscopy
Transmission electron microscopy is a microscopy technique whereby a beam of electrons is transmitted through an ultra thin specimen, interacting with the specimen as it passes through...
literature) for indexing hexagonal lattice vectors (rather than reciprocal lattice vectors or planes) with four indices. However they don't operate by similarly adding a redundant index to the regular three-index set.
For example, the reciprocal lattice vector (hkℓ) as suggested above can be written as ha*+kb*+lc*if the reciprocal-lattice basis-vectors are a*, b*, and c*. For hexagonal crystals this may be expressed in terms of direct-lattice basis-vectors a, b and c as
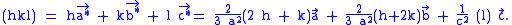
Hence zone indices of the direction perpendicular to plane (hkℓ) are, in suitably normalized triplet form, simply [2h+k,h+2k,l(3/2)(a/c)2]. When four indices are used for the zone normal to plane (hkℓ), however, the literature often uses [h,k,-h-k,l(3/2)(a/c)2] instead. Thus as you can see, four-index zone indices in square or angle brackets sometimes mix a single direct-lattice index on the right with reciprocal-lattice indices (normally in round or curly brackets) on the left.
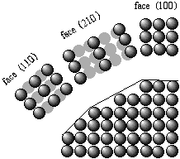
The crystallographic planes and directions
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
linking nodes (atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s, ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s or molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s) of a crystal. Similarly, the crystallographic planes
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
are fictitious planes linking nodes. Some directions and planes have a higher density of nodes; these dense planes have an influence on the behaviour of the crystal:
- optical propertiesOpticsOptics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
: in condensed matter, the lightLightLight or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
"jumps" from one atom to the other with the Rayleigh scatteringRayleigh scatteringRayleigh scattering, named after the British physicist Lord Rayleigh, is the elastic scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of the light. The particles may be individual atoms or molecules. It can occur when light travels through...
; the velocity of light thus varies according to the directions, whether the atoms are close or far; this gives the birefringenceBirefringenceBirefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite... - adsorptionAdsorptionAdsorption is the adhesion of atoms, ions, biomolecules or molecules of gas, liquid, or dissolved solids to a surface. This process creates a film of the adsorbate on the surface of the adsorbent. It differs from absorption, in which a fluid permeates or is dissolved by a liquid or solid...
and reactivity: the adsorption and the chemical reactions occur on atoms or molecules, these phenomena are thus sensitive to the density of nodes; - surface tensionSurface tensionSurface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
: the condensation of a material means that the atoms, ions or molecules are more stable if they are surrounded by other similar species; the surface tension of an interface thus varies according to the density on the surface- the porePore- Animal biology and microbiology :* Sweat pore, an anatomical structure of the skin of humans used for secretion of sweat* Canal pore, an anatomical structure that is part of the lateral line sense system of some aquatic organisms...
s and crystalliteCrystalliteCrystallites are small, often microscopic crystals that, held together through highly defective boundaries, constitute a polycrystalline solid. Metallurgists often refer to crystallites as grains.- Details :...
s tend to have straight grain boundaries following dense planes - cleavageCleavage (crystal)Cleavage, in mineralogy, is the tendency of crystalline materials to split along definite crystallographic structural planes. These planes of relative weakness are a result of the regular locations of atoms and ions in the crystal, which create smooth repeating surfaces that are visible both in the...
- the pore
- dislocationDislocationIn materials science, a dislocation is a crystallographic defect, or irregularity, within a crystal structure. The presence of dislocations strongly influences many of the properties of materials...
s (plastic deformation)- the dislocation core tends to spread on dense planes (the elastic perturbation is "diluted"); this reduces the frictionFrictionFriction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
(Peierls–Nabarro force), the sliding occurs more frequently on dense planes; - the perturbation carried by the dislocation (Burgers vectorBurgers vectorThe Burgers vector, named after Dutch physicist Jan Burgers, is a vector, often denoted b, that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice....
) is along a dense direction: the shift of one node in a dense direction is a lesser distortion; - the dislocation line tends to follow a dense direction, the dislocation line is often a straight line, a dislocation loop is often a polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
.
- the dislocation core tends to spread on dense planes (the elastic perturbation is "diluted"); this reduces the friction
For all these reasons, it is important to determine the planes and thus to have a notation system.
Integer vs. irrational Miller indices: Lattice planes and quasicrystals
Ordinarily, Miller indices are always integers by definition, and this constraint is physically significant. To understand this, suppose that we allow a plane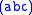
where the Miller "indices" a, b, and c (defined as above) are not necessarily integers.If a, b, and c have rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
ratios, then the same family of planes can be written in terms of integer indices (ℓmn) by scaling a, b, and c appropriately: divide by the largest of the three numbers, and then multiply by the least common denominator. Thus, integer Miller indices implicitly include indices with all rational ratios. The reason why planes where the components (in the reciprocal-lattice basis) have rational ratios are of special interest is that these are the lattice plane
Lattice plane
In crystallography, a lattice plane of a given Bravais lattice is a plane whose intersections with the lattice are periodic and intersect the Bravais lattice; equivalently, a lattice plane is any plane containing at least three noncollinear Bravais lattice points...
s: they are the only planes whose intersections with the crystal are 2d-periodic.
For a plane
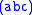where a, b, and c have irrationalIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
ratios, on the other hand, the intersection of the plane with the crystal is not periodic. It forms an aperiodic pattern known as a quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
. In fact, this construction corresponds precisely to the standard "cut-and-project" method of defining a quasicrystal, using a plane with irrational-ratio Miller indices. (Although many quasicrystals, such as the Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
, are formed by "cuts" of periodic lattices in more than three dimensions, involving the intersection of more than one such hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
.)
External links
- Miller index description with diagrams
- Online tutorial about lattice planes and Miller indices.
- MTEX – Free MATLAB toolbox for Texture Analysis
- http://sourceforge.net/projects/orilib – A collection of routines for rotation / orientation manipulation, including special tools for crystal orientations.