
Clebsch-Gordan coefficients
Encyclopedia
In physics
, the Clebsch–Gordan coefficients are sets of numbers that arise in angular momentum coupling
under the laws of quantum mechanics
.
In more mathematical terms, the CG coefficients are used in representation theory
, particularly of compact Lie groups, to perform the explicit direct sum decomposition of the tensor product
of two irreducible representations into irreducible representations, in cases where the numbers and types of irreducible components are already known abstractly. The name derives from the German mathematicians Alfred Clebsch
(1833–1872) and Paul Gordan (1837–1912), who encountered an equivalent problem in invariant theory
.
In terms of classical mathematics, the CG coefficients, or at least those associated to the group SO(3), may be defined much more directly, by means of formulae for the multiplication of spherical harmonic
s. The addition of spins in quantum-mechanical terms can be read directly from this approach. The formulas below use Dirac's
bra-ket notation
.
total angular momentum eigenstates in an
uncoupled tensor product basis.
Below, this definition is made precise by defining angular momentum
operators, angular momentum eigenstates, and tensor products of these states.
From the formal definition of angular momentum, recursion relations for the Clebsch–Gordan coefficients
can be found. To find numerical values for the coefficients a phase convention
must be adopted. Below the Condon–Shortley phase convention is chosen.
s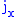 ,
, 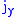 ,
,
and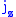 that satisfy the commutation relations
that satisfy the commutation relations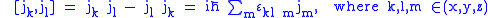
where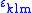 is the Levi-Civita symbol. Together the three operators define a "vector operator":
is the Levi-Civita symbol. Together the three operators define a "vector operator":

By developing this concept further, one can define an operator as an "inner product" of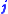 with itself:
with itself:
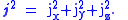
It is an example of a Casimir operator.
We also define raising (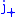 ) and lowering (
) and lowering (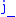 ) operators:
) operators:
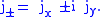
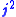 commutes with
commutes with  ,
, 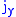
and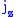

When two Hermitian operators commute a common set of eigenfunctions exists.
Conventionally and
and 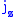 are chosen.
are chosen.
From the commutation relations the possible eigenvalues can be found.
The result is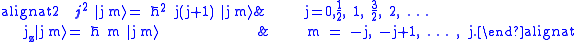
The raising and lowering operators change the value of
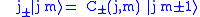
with
A (complex) phase factor could be included in the definition of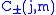
The choice made here is in agreement with the Condon and Shortley phase conventions.
The angular momentum states must be orthogonal (because their eigenvalues with
respect to a Hermitian operator are distinct) and they are assumed to be normalized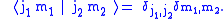
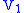 be the
be the 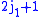 dimensional
dimensional
vector space spanned by the states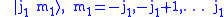
and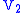 the
the  dimensional
dimensional
vector space spanned by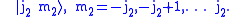
The tensor product of these spaces,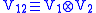 ,
,
has a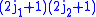 dimensional uncoupled basis
dimensional uncoupled basis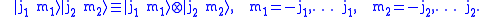
Angular momentum operators acting on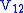 can be defined by
can be defined by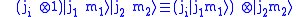
and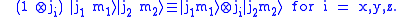
Total angular momentum operators are defined by
The total angular momentum operators satisfy the required commutation relations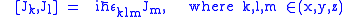
and hence total angular momentum eigenstates exist
It can be derived that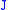 must satisfy the triangular condition
must satisfy the triangular condition
The total number of total angular momentum eigenstates is equal to the dimension
of
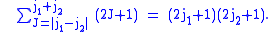
The total angular momentum states form an orthonormal basis of
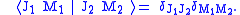
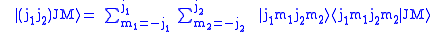
The expansion coefficients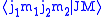
are called Clebsch–Gordan coefficients.
Applying the operator
to both sides of the defining equation shows that the Clebsch–Gordan coefficients
can only be nonzero when
Applying the total angular momentum raising and lowering operators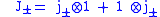
to the left hand side of the defining equation gives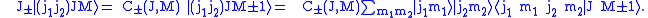
Applying the same operators to the right hand side gives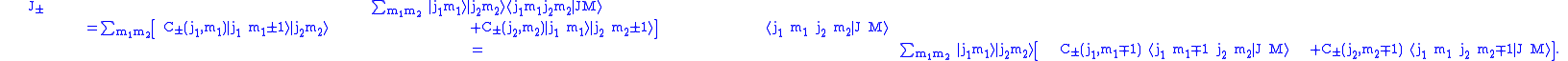
where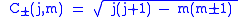
Combining these results gives recursion relations for the Clebsch–Gordan
coefficients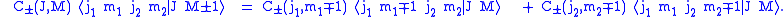
Taking the upper sign with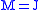 gives
gives
In the Condon and Shortley phase convention the coefficient
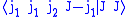 is taken
is taken
real and positive. With the last equation all other
Clebsch–Gordan coefficients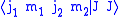
can be found. The normalization is fixed by the requirement that
the sum of the squares, which corresponds to the norm of the
state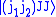 must be one.
must be one.
The lower sign in the recursion relation can be used to find
all the Clebsch–Gordan coefficients with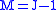 .
.
Repeated use of that equation gives all coefficients.
This procedure to find the Clebsch–Gordan coefficients shows that
they are all real (in the Condon and Shortley phase convention).
and tables with numerical values, see
table of Clebsch–Gordan coefficients.
alternative notation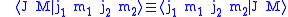
The first orthogonality relation is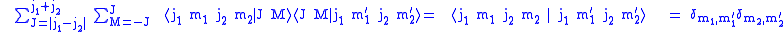
(using the completeness relation that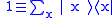 )and the second
)and the second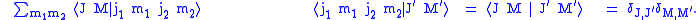
 the Clebsch–Gordan coefficients are given by
the Clebsch–Gordan coefficients are given by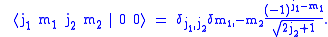
For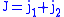 and
and  we have
we have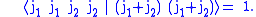
For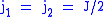 and
and 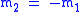 we have
we have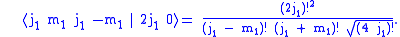
For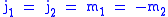 we have
we have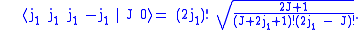
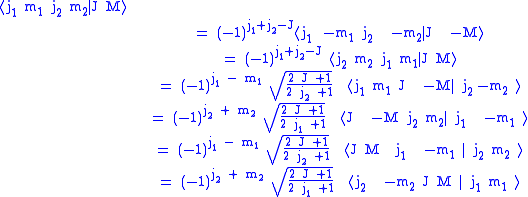
A convenient way to derive these relations is by converting
the Clebsch–Gordan coefficients to 3-jm symbols using the equation
given below. The symmetry properties of 3-jm symbols are much simpler.
Care is needed when simplifying phase factors, because the
quantum numbers can be integer or half integer, e.g.,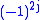
is equal to 1 for integer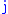 and
and
equal to −1 for half-integer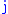 . The
. The
following relations, however, are valid in either case: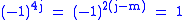
and for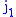 ,
, 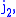 and
and 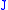 appearing in the
appearing in the
same Clebsch–Gordan coefficient: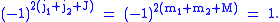
more convenient symmetry relations.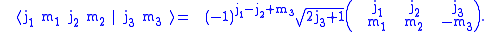
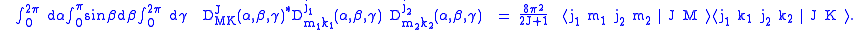
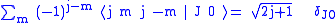
are known. A web interface for tabulating SU(N) Clebsch–Gordan coefficients is readily available.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Clebsch–Gordan coefficients are sets of numbers that arise in angular momentum coupling
Angular momentum coupling
In quantum mechanics, the procedure of constructing eigenstates of total angular momentum out of eigenstates of separate angular momenta is called angular momentum coupling. For instance, the orbit and spin of a single particle can interact through spin-orbit interaction, in which case the...
under the laws of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
In more mathematical terms, the CG coefficients are used in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, particularly of compact Lie groups, to perform the explicit direct sum decomposition of the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of two irreducible representations into irreducible representations, in cases where the numbers and types of irreducible components are already known abstractly. The name derives from the German mathematicians Alfred Clebsch
Alfred Clebsch
Rudolf Friedrich Alfred Clebsch was a German mathematician who made important contributions to algebraic geometry and invariant theory. He attended the University of Königsberg and was habilitated at Berlin. He subsequently taught in Berlin and Karlsruhe...
(1833–1872) and Paul Gordan (1837–1912), who encountered an equivalent problem in invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
.
In terms of classical mathematics, the CG coefficients, or at least those associated to the group SO(3), may be defined much more directly, by means of formulae for the multiplication of spherical harmonic
Spherical Harmonic
Spherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
s. The addition of spins in quantum-mechanical terms can be read directly from this approach. The formulas below use Dirac's
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
.
Clebsch–Gordan coefficients
Clebsch–Gordan coefficients are the expansion coefficients oftotal angular momentum eigenstates in an
uncoupled tensor product basis.
Below, this definition is made precise by defining angular momentum
operators, angular momentum eigenstates, and tensor products of these states.
From the formal definition of angular momentum, recursion relations for the Clebsch–Gordan coefficients
can be found. To find numerical values for the coefficients a phase convention
must be adopted. Below the Condon–Shortley phase convention is chosen.
Angular momentum operators
Angular momentum operators are self-adjoint operatorSelf-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s
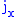 ,
, 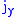 ,
,and
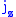 that satisfy the commutation relations
that satisfy the commutation relations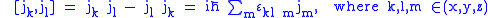
where
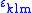 is the Levi-Civita symbol. Together the three operators define a "vector operator":
is the Levi-Civita symbol. Together the three operators define a "vector operator":
By developing this concept further, one can define an operator as an "inner product" of
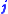 with itself:
with itself: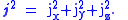
It is an example of a Casimir operator.
We also define raising (
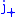 ) and lowering (
) and lowering (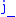 ) operators:
) operators: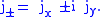
Angular momentum states
It can be shown from the above definitions that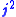 commutes with
commutes with  ,
, 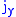
and
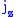

When two Hermitian operators commute a common set of eigenfunctions exists.
Conventionally
 and
and 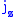 are chosen.
are chosen.From the commutation relations the possible eigenvalues can be found.
The result is
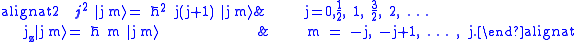
The raising and lowering operators change the value of

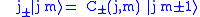
with

A (complex) phase factor could be included in the definition of
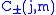
The choice made here is in agreement with the Condon and Shortley phase conventions.
The angular momentum states must be orthogonal (because their eigenvalues with
respect to a Hermitian operator are distinct) and they are assumed to be normalized
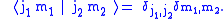
Tensor product space
Let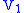 be the
be the 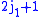 dimensional
dimensionalvector space spanned by the states
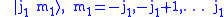
and
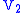 the
the  dimensional
dimensionalvector space spanned by
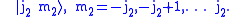
The tensor product of these spaces,
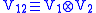 ,
,has a
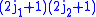 dimensional uncoupled basis
dimensional uncoupled basis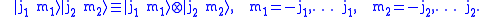
Angular momentum operators acting on
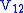 can be defined by
can be defined by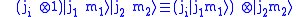
and
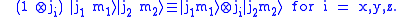
Total angular momentum operators are defined by

The total angular momentum operators satisfy the required commutation relations
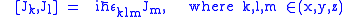
and hence total angular momentum eigenstates exist

It can be derived that
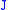 must satisfy the triangular condition
must satisfy the triangular condition
The total number of total angular momentum eigenstates is equal to the dimension
of

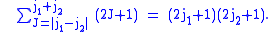
The total angular momentum states form an orthonormal basis of

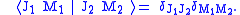
Formal definition of Clebsch–Gordan coefficients
The total angular momentum states can be expanded with the use of the completeness relation in the uncoupled basis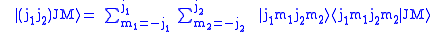
The expansion coefficients
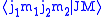
are called Clebsch–Gordan coefficients.
Applying the operator

to both sides of the defining equation shows that the Clebsch–Gordan coefficients
can only be nonzero when
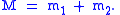
Recursion relations
The recursion relations were discovered by the physicist Giulio Racah.Applying the total angular momentum raising and lowering operators
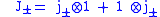
to the left hand side of the defining equation gives
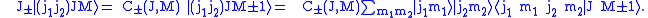
Applying the same operators to the right hand side gives
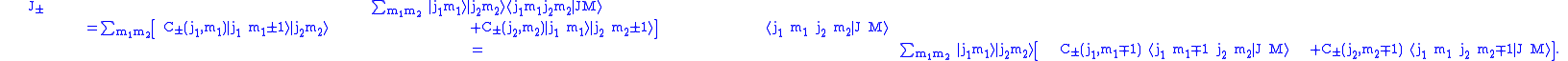
where
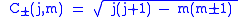
Combining these results gives recursion relations for the Clebsch–Gordan
coefficients
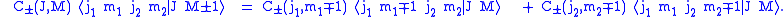
Taking the upper sign with
 gives
gives
In the Condon and Shortley phase convention the coefficient
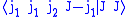 is taken
is takenreal and positive. With the last equation all other
Clebsch–Gordan coefficients
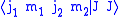
can be found. The normalization is fixed by the requirement that
the sum of the squares, which corresponds to the norm of the
state
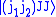 must be one.
must be one.The lower sign in the recursion relation can be used to find
all the Clebsch–Gordan coefficients with
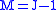 .
.Repeated use of that equation gives all coefficients.
This procedure to find the Clebsch–Gordan coefficients shows that
they are all real (in the Condon and Shortley phase convention).
Explicit expression
For an explicit expression of the Clebsch–Gordan coefficientsand tables with numerical values, see
table of Clebsch–Gordan coefficients.
Orthogonality relations
These are most clearly written down by introducing thealternative notation
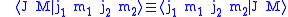
The first orthogonality relation is
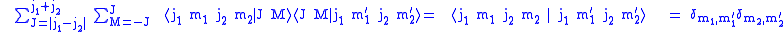
(using the completeness relation that
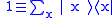 )and the second
)and the second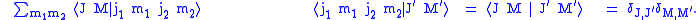
Special cases
For the Clebsch–Gordan coefficients are given by
the Clebsch–Gordan coefficients are given by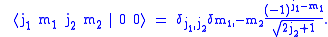
For
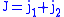 and
and  we have
we have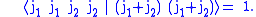
For
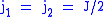 and
and 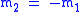 we have
we have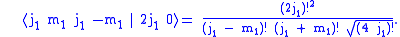
For
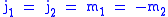 we have
we have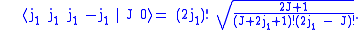
Symmetry properties
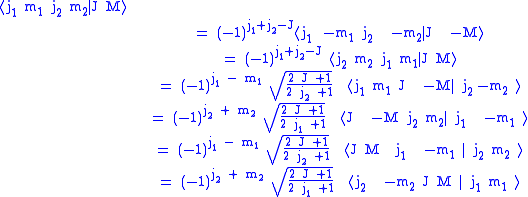
A convenient way to derive these relations is by converting
the Clebsch–Gordan coefficients to 3-jm symbols using the equation
given below. The symmetry properties of 3-jm symbols are much simpler.
Care is needed when simplifying phase factors, because the
quantum numbers can be integer or half integer, e.g.,
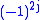
is equal to 1 for integer
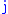 and
andequal to −1 for half-integer
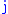 . The
. Thefollowing relations, however, are valid in either case:
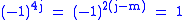
and for
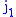 ,
, 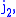 and
and 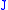 appearing in the
appearing in thesame Clebsch–Gordan coefficient:
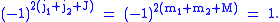
Relation to 3-jm symbols
Clebsch–Gordan coefficients are related to 3-jm symbols which havemore convenient symmetry relations.
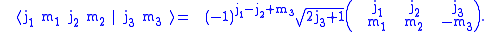
Relation to Wigner D-matrices
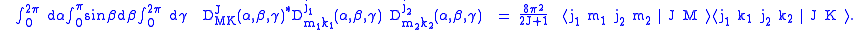
Other Properties
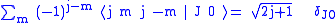
SU(N) Clebsch–Gordan coefficients
For arbitrary groups and their representations, Clebsch–Gordan coefficients are not known in general. However, algorithms to produce Clebsch–Gordan coefficients for the Special unitary groupSpecial unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
are known. A web interface for tabulating SU(N) Clebsch–Gordan coefficients is readily available.

