Classification of electromagnetic fields
Encyclopedia
In differential geometry and theoretical physics
, the classification of electromagnetic fields is a pointwise classification of bivector
s at each point of a Lorentzian manifold.
It is used in the study of solutions of Maxwell's equations
and has applications in Einstein's theory of general relativity
, but the theorem is a purely mathematical one.
, ra → Fabrb. Here, the vector space is the tangent space at the given event, and thus isomorphic as a (real) inner product space to E1,3. That is, it has the same notion of vector magnitude
and angle
(or inner product) as Minkowski spacetime.
In the remainder of this section (and in the next section), we'll assume our spacetime is Minkowski spacetime. This simplifies the mathematics (but tends to blur the distinction between the tangent space at an event and the underlying manifold). Fortunately, nothing will be lost by this apparently drastic specialization, for reasons we discuss as the end of the article.
In studying any linear operator, we confront the eigenvalue problem, that is, the problem of finding eigenvalues λ and eigenvectors r which satisfy the eigenvalue equation
The skew-symmetry of the operator we are interested in now implies that one of the following must hold:
The linearly independent null eigenspaces are called the principal null directions of the bivector.
The classification theorem characterizes the possible principal null directions of a bivector. It states that one of the following must hold for any nonzero bivector:
Furthermore, for any non-null bivector, the two eigenvalues associated with the two distinct principal null directions have the same magnitude but opposite sign, λ = ±ν, so we have three subclasses of non-null bivectors:
where the rank refers to the rank
of the linear operator F. Every nonsimple bivector can be written as a sum of at most two simple ones.
is represented by a skew-symmetric second rank tensor (the electromagnetic field tensor) so we immediately obtain an algebraic classification of electromagnetic fields.
Recall that for in a cartesian chart on Minkowski spacetime, the electromagnetic field tensor has components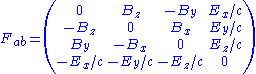
where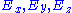
and 
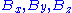denote respectively the components of the electric and magnetic fields, as measured by an inertial observer (at rest in our coordinates). As usual in relativistic physics, we will find it convenient to work with geometrised units
in which
. In the "tensor gymanastics" formalism of special relativity, the Minkowski metric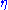 
is used to raise and lower indices.
.
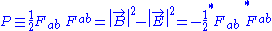
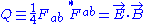(Fundamental means that every other invariant can be expressed in terms of these two.)
A null electromagnetic field is characterised by
. In this case, the invariants reveal that the electric and magnetic fields are perpendicular and that they are of the same magnitude (in geometrised units). An example of a null field is a plane electromagnetic wave
in Minkowski space
.
A non-null field is characterised by
. If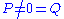 
, there exists an inertial frame for which either the electric or magnetic field vanishes. (These correspond respectively to magnetostatic and electrostatic fields.) If 
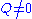, there exists an inertial frame in which electric and magnetic fields are proportional.
, everything works out exactly the same way on curved manifolds.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the classification of electromagnetic fields is a pointwise classification of bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s at each point of a Lorentzian manifold.
It is used in the study of solutions of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and has applications in Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, but the theorem is a purely mathematical one.
The classification theorem
A (real) bivector field may be viewed, at any given event in a spacetime, as a skew-symmetric linear operator on a four-dimensional (real) vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, ra → Fabrb. Here, the vector space is the tangent space at the given event, and thus isomorphic as a (real) inner product space to E1,3. That is, it has the same notion of vector magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
and angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
(or inner product) as Minkowski spacetime.
In the remainder of this section (and in the next section), we'll assume our spacetime is Minkowski spacetime. This simplifies the mathematics (but tends to blur the distinction between the tangent space at an event and the underlying manifold). Fortunately, nothing will be lost by this apparently drastic specialization, for reasons we discuss as the end of the article.
In studying any linear operator, we confront the eigenvalue problem, that is, the problem of finding eigenvalues λ and eigenvectors r which satisfy the eigenvalue equation
The skew-symmetry of the operator we are interested in now implies that one of the following must hold:
- r is a null vector belonging to a nonzero eigenvalue
- r is a nonnull eigenvector belonging to the eigenvalue zero
- r is a null eigenvector belonging to the eigenvalue zero
The linearly independent null eigenspaces are called the principal null directions of the bivector.
The classification theorem characterizes the possible principal null directions of a bivector. It states that one of the following must hold for any nonzero bivector:
- one repeated principal null direction, in this case, the bivector is said to be null,
- two distinct principal null directions, in this case, the bivector is said to be non-null.
Furthermore, for any non-null bivector, the two eigenvalues associated with the two distinct principal null directions have the same magnitude but opposite sign, λ = ±ν, so we have three subclasses of non-null bivectors:
- spacelike: ν = 0
- timelike : ν ≠ 0 and rank F = 2
- non-simple: ν ≠ 0 and rank F = 4
where the rank refers to the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of the linear operator F. Every nonsimple bivector can be written as a sum of at most two simple ones.
Physical interpretation
The algebraic classification of bivectors given above has an important application in relativistic physics: the electromagnetic fieldElectromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
is represented by a skew-symmetric second rank tensor (the electromagnetic field tensor) so we immediately obtain an algebraic classification of electromagnetic fields.
Recall that for in a cartesian chart on Minkowski spacetime, the electromagnetic field tensor has components
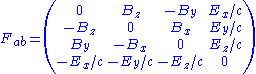
where
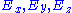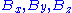and denote respectively the components of the electric and magnetic fields, as measured by an inertial observer (at rest in our coordinates). As usual in relativistic physics, we will find it convenient to work with geometrised unitsGeometrized unit system
A geometrized unit system or geometric unit system is a system of natural units in which the base physical units are chosen so that the speed of light in a vacuum, c, and the gravitational constant, G, are set equal to unity. c = 1 \ G = 1 \...
in which
. In the "tensor gymanastics" formalism of special relativity, the Minkowski metric 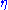is used to raise and lower indices.Invariants
The fundamental invariants of the electromagnetic field are: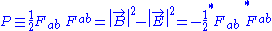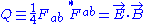.(Fundamental means that every other invariant can be expressed in terms of these two.)
A null electromagnetic field is characterised by
. In this case, the invariants reveal that the electric and magnetic fields are perpendicular and that they are of the same magnitude (in geometrised units). An example of a null field is a plane electromagnetic wavePlane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
A non-null field is characterised by
. If 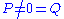, there exists an inertial frame for which either the electric or magnetic field vanishes. (These correspond respectively to magnetostatic and electrostatic fields.) If 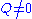, there exists an inertial frame in which electric and magnetic fields are proportional.Curved Lorentzian manifolds
So far we have discussed only flat spacetime, i.e. the Minkowski vacuum. Fortunately, according to the (strong) equivalence principle, if we simply replace "inertial frame" above with a frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
, everything works out exactly the same way on curved manifolds.
See also
- Electromagnetic peeling theorem
- Electrovacuum solutionElectrovacuum solutionIn general relativity, an electrovacuum solution is an exact solution of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field, which must satisfy the source-free Maxwell equations appropriate to the given geometry...
- Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
- Petrov classificationPetrov classificationIn differential geometry and theoretical physics, the Petrov classification describes the possible algebraic symmetries of the Weyl tensor at each event in a Lorentzian manifold....