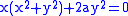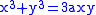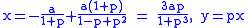Cissoid
Encyclopedia
In geometry
, a cissoid is a curve generated from two given curves C1, C2 and a point O (the pole). Let L be a variable line passing through O and intersecting C1 at P1 and C2 at P2. Let P be the point on L so that OP = P1P2. (There are actually two such points but P is chosen so that P is in the same direction from O as P2 is from P1.) Then the locus of such points P is defined to be the cissoid of the curves C1, C2 relative to O.
Slightly different but essentially equivalent definitions are used by different authors. For example, P may be defined to be the point so that OP = OP1 + OP2. This is equivalent to the other definition if C1 is replaced by its reflection
through O. Or P may be defined as the midpoint of P1 and P2; this produces the curve generated by the previous curve scaled by a factor of 1/2.
The word "cissoid" comes from the Greek
kissoeidēs "ivy
shaped" from kissos "ivy" and -oeidēs "having the likeness of".
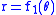and 
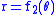respectively, then the equation 
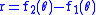describes the cissoid of C1 and C2 relative to the origin. However, because a point may be represented in multiple ways in polar coordinates, there may be other branches of the cissoid which have a different equation. Specifically, C1 is also given by
.
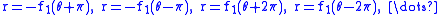So the cissoid is actually the union of the curves given by the equations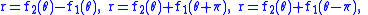
.
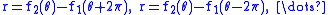It can be determined on an individual basis depending on the periods of f1 and f2, which of these equations can be eliminated due to duplication.
For example, let C1 and C2 both be the ellipse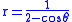
.
The first branch of the cissoid is given by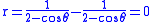
,
which is simply the origin. The ellipse is also given by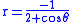
,
so a second branch of the cissoid is given by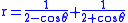
which is an oval shaped curve.
If each C1 and C2 are given by the parametric equations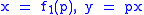
and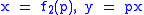
,
then the cissoid relative to the origin is given by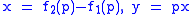
.
of C2.
When C1 and C2 are parallel lines then the cissoid is a third line parallel to the given lines.
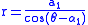
and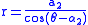
.
By rotation through angle
, we can assume that 
. Then the cissoid of C1 and C2 relative to the origin is given by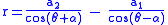
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a cissoid is a curve generated from two given curves C1, C2 and a point O (the pole). Let L be a variable line passing through O and intersecting C1 at P1 and C2 at P2. Let P be the point on L so that OP = P1P2. (There are actually two such points but P is chosen so that P is in the same direction from O as P2 is from P1.) Then the locus of such points P is defined to be the cissoid of the curves C1, C2 relative to O.
Slightly different but essentially equivalent definitions are used by different authors. For example, P may be defined to be the point so that OP = OP1 + OP2. This is equivalent to the other definition if C1 is replaced by its reflection
Point reflection
In geometry, a point reflection or inversion in a point is a type of isometry of Euclidean space...
through O. Or P may be defined as the midpoint of P1 and P2; this produces the curve generated by the previous curve scaled by a factor of 1/2.
The word "cissoid" comes from the Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
kissoeidēs "ivy
Ivy
Ivy, plural ivies is a genus of 12–15 species of evergreen climbing or ground-creeping woody plants in the family Araliaceae, native to western, central and southern Europe, Macaronesia, northwestern Africa and across central-southern Asia east to Japan and Taiwan.-Description:On level ground they...
shaped" from kissos "ivy" and -oeidēs "having the likeness of".
Equations
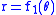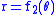If C1 and C2 are given in polar coordinates by and respectively, then the equation 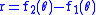describes the cissoid of C1 and C2 relative to the origin. However, because a point may be represented in multiple ways in polar coordinates, there may be other branches of the cissoid which have a different equation. Specifically, C1 is also given by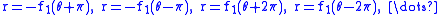.So the cissoid is actually the union of the curves given by the equations
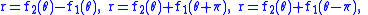
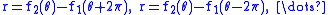.It can be determined on an individual basis depending on the periods of f1 and f2, which of these equations can be eliminated due to duplication.
For example, let C1 and C2 both be the ellipse
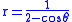.The first branch of the cissoid is given by
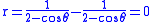,which is simply the origin. The ellipse is also given by
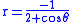,so a second branch of the cissoid is given by
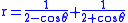
which is an oval shaped curve.
If each C1 and C2 are given by the parametric equations
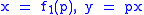
and
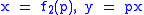,then the cissoid relative to the origin is given by
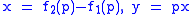.Specific cases
When C1 is a circle with center O then the cissoid is conchoidConchoid (mathematics)
A conchoid is a curve derived from a fixed point O, another curve, and a length d. For every line through O that intersects the given curve at A the two points on the line which are d from A are on the conchoid. The conchoid is, therefore, the cissoid of a circle with center O and the given curve...
of C2.
When C1 and C2 are parallel lines then the cissoid is a third line parallel to the given lines.
Hyperbolas
Let C1 and C2 be two non-parallel lines and let O be the origin. Let the polar equations of C1 and C2 be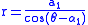and
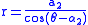.By rotation through angle
, we can assume that . Then the cissoid of C1 and C2 relative to the origin is given by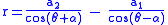
-
.
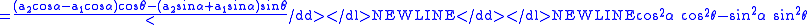Combining constants gives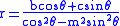
which in Cartesian coordinates is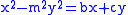
.
This is a hyperbola passing though the origin. So the cissoid of two non-parallel lines is a hyperbola containing the pole. A similar derivation show that, conversely, any hyperbola is the cissoid of two non-parallel lines relative to any point on it.
Cissoids of Zahradnik
A cissoid of Zahradnik (name after Karel ZahradnikKarel ZahradnikKarel Zahradnik was a renowned Czech mathematician at the University of Zagreb. In his 23 years of productive activity in Zagreb he wrote several significant scholarly works, mainly concerned with algebraic curves.-Further reading:...
) is defined as the cissoid of a conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
and a line relative to any point on the conic. This is a broad family of rational cubic curves containing several well known examples. Specifically:- The Trisectrix of MaclaurinTrisectrix of MaclaurinIn geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the...
given by
-
- is the cissoid of the circle
and the line 
relative to the origin.
- The right strophoid
-
- is the cissoid of the circle
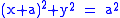and the line 
relative to the origin.
- The cissoid of DioclesCissoid of DioclesIn geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the...
-
- is the cissoid of the circle
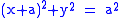and the line 
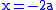relative to the origin. This is, in fact, the curve for which the family is named and some authors refer to this as simply as cissoid.
- The cissoid of the circle
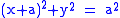and the line 
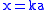, where k is a parameter, is called a Conchoid of de SluzeConchoid of de SluzeThe conchoid of de Sluze is a family of plane curves studied in 1662 by René François Walter, baron de Sluze.The curves are defined by the polar equationr=\sec\theta+a\cos\theta \,....
. (These curves are not actually concoids.) This family includes the previous examples.
- The folium of DescartesFolium of DescartesIn geometry, the Folium of Descartes is an algebraic curve defined by the equationx^3 + y^3 - 3 a x y = 0 \,.It forms a loop in the first quadrant with a double point at the origin and asymptotex + y + a = 0 \,.It is symmetrical about y = x....
-
- is the cissoid of the ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
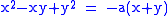and the line 
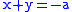relative to the origin. To see this, note that the line can be written
- and the ellipse can written
.
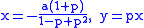- So the cissoid is given by
- which is a parametric form of the folium.
External links
- The Trisectrix of Maclaurin
