Channel state information
Encyclopedia
In wireless communications, channel state information (CSI) refers to known channel properties of a communication link. This information describes how a signal propagates from the transmitter to the receiver and represents the combined effect of, for example, scattering
, fading
, and power decay with distance. The CSI makes it possible to adapt transmissions to current channel conditions, which is crucial for achieving reliable communication with high data rates
in multiantenna systems
.
CSI needs to be estimated at the receiver and usually quantized
and fed back
to the transmitter (although reverse-link estimation is possible in TDD systems). Therefore, the transmitter and receiver can have different CSI. The CSI at the transmitter and the CSI at the receiver are sometimes referred to as CSIT and CSIR, respectively.
Instantaneous CSI (or short-term CSI) means that the current channel conditions are known, which can be viewed as knowing the impulse response
of a digital filter
. This gives an opportunity to adapt the transmitted signal to the impulse response and thereby optimize the received signal for spatial multiplexing
or to achieve low bit error rates.
Statistical CSI (or long-term CSI) means that a statistical characterization of the channel is known. This description can include, for example, the type of fading distribution, the average channel gain, the line-of-sight component
, and the spatial correlation
. As with instantaneous CSI, this information can be used for transmission optimization.
The CSI acquisition is practically limited by how fast the channel conditions are changing. In fast fading systems where channel conditions vary rapidly under the transmission of a single information symbol, only statistical CSI is reasonable. On the other hand, in slow fading systems instantaneous CSI can be estimated with reasonable accuracy and used for transmission adaptation for some time before being outdated.
In practical systems, the available CSI often lies in between these two levels; instantaneous CSI with some estimation/quantization error is combined with statistical information.
flat-fading channel with multiple transmit and receive antennas (MIMO), the system is modeled as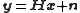
where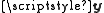
and 
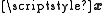are the receive and transmit vectors, respectively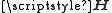, and 
and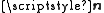 
are the channel matrix and the noise vector, respectively. The noise is often modeled as circular symmetric complex normal
with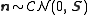
where the mean value is zero and the noise covariance matrix
is known.
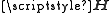is known perfectly. Due to channel estimation errors, the channel information can be represented as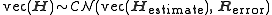
where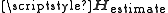
is the channel estimate and 
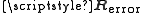is the estimation error covariance matrix. The vectorization
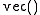was used to achieve the column stacking of 
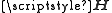, as multivariate random variable
s are usually defined as vectors.
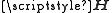are known. In a Rayleigh fading
channel, this corresponds to knowing that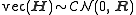
for some known channel covariance matrix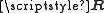
.
on a short-term basis. A popular approach is so-called training sequence (or pilot sequence), where a known signal is transmitted and the channel matrix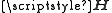
is estimated using the combined knowledge of the transmitted and received signal.
Let the training sequence be denoted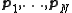
, where the vector 
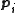is transmitted over the channel as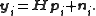
By combining the received training signals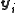
for 
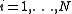, the total training signalling becomes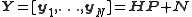
with the training matrix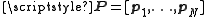
and the noise matrix 
.
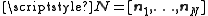With this notation, channel estimation means that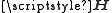
should be recovered from the knowledge of 
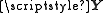and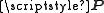 
.
estimator (also known as the minimum-variance unbiased estimator
) is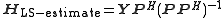
where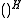
denotes the conjugate transpose
. The estimation Mean Square Error
(MSE) is proportional to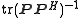
where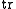
denotes the trace
. The error is minimized when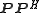
is a scaled identity matrix
. This can only be achieved when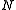
is equal to (or larger than) the number of transmit antennas. The simplest example of an optimal training matrix is to select 
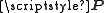as a (scaled) identity matrix of the same size that the number of transmit antennas.
can be exploited to decrease the estimation error. This approach is known as Bayesian estimation and for Rayleigh fading channels it exploits that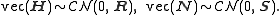
The MMSE estimator is the Bayesian counterpart to the least-square estimator and becomes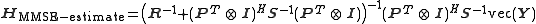
where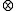
denotes the Kronecker product
and the identity matrix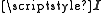
has the dimension of the number of receive antennas. The estimation Mean Square Error
(MSE) is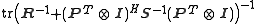
and is minimized by a training matrix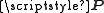
that in general can only be derived through numerical optimization. But there exist heuristic solutions with good performance based on waterfilling. As opposed to least-square estimation, the estimation error for spatially correlated
channels can be minimized even if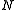
is smaller than the number of transmit antennas. Thus, MMSE estimation can both decrease the estimation error and shorten the required training sequence. It needs however additionally the knowledge of the channel correlation matrix 
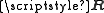and noise correlation matrix 
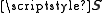. In absence of an accurate knowledge of these correlation matrices, robust choices need to be made to avoid MSE degradation.
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
, fading
Fading
In wireless communications, fading is deviation of the attenuation that a carrier-modulated telecommunication signal experiences over certain propagation media. The fading may vary with time, geographical position and/or radio frequency, and is often modelled as a random process. A fading channel...
, and power decay with distance. The CSI makes it possible to adapt transmissions to current channel conditions, which is crucial for achieving reliable communication with high data rates
Bit rate
In telecommunications and computing, bit rate is the number of bits that are conveyed or processed per unit of time....
in multiantenna systems
MIMO
In radio, multiple-input and multiple-output, or MIMO , is the use of multiple antennas at both the transmitter and receiver to improve communication performance. It is one of several forms of smart antenna technology...
.
CSI needs to be estimated at the receiver and usually quantized
Quantization (signal processing)
Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set – such as rounding values to some unit of precision. A device or algorithmic function that performs quantization is called a quantizer. The error introduced by...
and fed back
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
to the transmitter (although reverse-link estimation is possible in TDD systems). Therefore, the transmitter and receiver can have different CSI. The CSI at the transmitter and the CSI at the receiver are sometimes referred to as CSIT and CSIR, respectively.
Different kinds of channel state information
There are basically two levels of CSI, namely instantaneous CSI and statistical CSI.Instantaneous CSI (or short-term CSI) means that the current channel conditions are known, which can be viewed as knowing the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of a digital filter
Digital filter
In electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
. This gives an opportunity to adapt the transmitted signal to the impulse response and thereby optimize the received signal for spatial multiplexing
Spatial multiplexing
Spatial multiplexing is a transmission technique in MIMO wireless communication to transmit independent and separately encoded data signals, so-called streams, from each of the multiple transmit antennas...
or to achieve low bit error rates.
Statistical CSI (or long-term CSI) means that a statistical characterization of the channel is known. This description can include, for example, the type of fading distribution, the average channel gain, the line-of-sight component
Line-of-sight propagation
Line-of-sight propagation refers to electro-magnetic radiation or acoustic wave propagation. Electromagnetic transmission includes light emissions traveling in a straight line...
, and the spatial correlation
Spatial Correlation
Theoretically, the performance of wireless communication systems can be improved by having multiple antennas at the transmitter and the receiver. The idea is that if the propagation channels between each pair of transmit and receive antennas are statistically independent and identically...
. As with instantaneous CSI, this information can be used for transmission optimization.
The CSI acquisition is practically limited by how fast the channel conditions are changing. In fast fading systems where channel conditions vary rapidly under the transmission of a single information symbol, only statistical CSI is reasonable. On the other hand, in slow fading systems instantaneous CSI can be estimated with reasonable accuracy and used for transmission adaptation for some time before being outdated.
In practical systems, the available CSI often lies in between these two levels; instantaneous CSI with some estimation/quantization error is combined with statistical information.
Mathematical description
In a narrowbandNarrowband
In radio, narrowband describes a channel in which the bandwidth of the message does not significantly exceed the channel's coherence bandwidth. It is a common misconception that narrowband refers to a channel which occupies only a "small" amount of space on the radio spectrum.The opposite of...
flat-fading channel with multiple transmit and receive antennas (MIMO), the system is modeled as
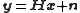
where
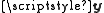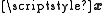and are the receive and transmit vectors, respectively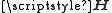, and and 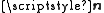are the channel matrix and the noise vector, respectively. The noise is often modeled as circular symmetric complex normalComplex normal distribution
In probability theory, the family of complex normal distributions consists of complex random variables whose real and imaginary parts are jointly normal. The complex normal family has three parameters: location parameter μ, covariance matrix Γ, and the relation matrix C...
with
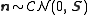
where the mean value is zero and the noise covariance matrix
is known.Instantaneous CSI
Ideally, the channel matrix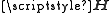 is known perfectly. Due to channel estimation errors, the channel information can be represented as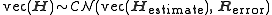where
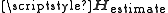is the channel estimate and 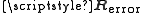is the estimation error covariance matrix. The vectorizationVectorization (mathematics)
In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector...
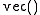was used to achieve the column stacking of 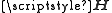, as multivariate random variableMultivariate random variable
In mathematics, probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose values is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value.More formally, a multivariate random...
s are usually defined as vectors.
Statistical CSI
In this case, the statistics of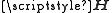 are known. In a Rayleigh fadingRayleigh fading
Rayleigh fading is a statistical model for the effect of a propagation environment on a radio signal, such as that used by wireless devices.Rayleigh fading models assume that the magnitude of a signal that has passed through such a transmission medium will vary randomly, or fade, according to a...
channel, this corresponds to knowing that
for some known channel covariance matrix
.Estimation of CSI
Since the channel conditions vary, instantaneous CSI needs to be estimatedEstimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
on a short-term basis. A popular approach is so-called training sequence (or pilot sequence), where a known signal is transmitted and the channel matrix
is estimated using the combined knowledge of the transmitted and received signal.Let the training sequence be denoted
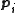, where the vector is transmitted over the channel as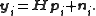By combining the received training signals
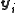for 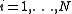, the total training signalling becomes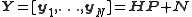with the training matrix
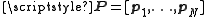and the noise matrix 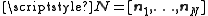.With this notation, channel estimation means that
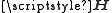should be recovered from the knowledge of 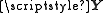and 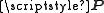.Least-square estimation
If the channel and noise distributions are unknown, then the least-squareLeast squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
estimator (also known as the minimum-variance unbiased estimator
Minimum-variance unbiased estimator
In statistics a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.The question of determining the UMVUE, if one exists, for a particular...
) is
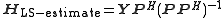
where
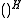denotes the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
. The estimation Mean Square Error
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
(MSE) is proportional to
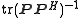
where
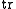denotes the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
. The error is minimized when
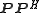is a scaled identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. This can only be achieved when
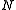is equal to (or larger than) the number of transmit antennas. The simplest example of an optimal training matrix is to select 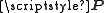as a (scaled) identity matrix of the same size that the number of transmit antennas.MMSE estimation
If the channel and noise distributions are known, then this a priori informationA priori (statistics)
In statistics, a priori knowledge is prior knowledge about a population, rather than that estimated by recent observation. It is common in Bayesian inference to make inferences conditional upon this knowledge, and the integration of a priori knowledge is the central difference between the Bayesian...
can be exploited to decrease the estimation error. This approach is known as Bayesian estimation and for Rayleigh fading channels it exploits that
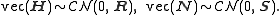
The MMSE estimator is the Bayesian counterpart to the least-square estimator and becomes
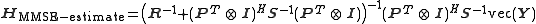
where
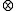denotes the Kronecker productKronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
and the identity matrix
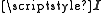has the dimension of the number of receive antennas. The estimation Mean Square ErrorMean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
(MSE) is
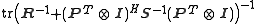
and is minimized by a training matrix
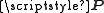that in general can only be derived through numerical optimization. But there exist heuristic solutions with good performance based on waterfilling. As opposed to least-square estimation, the estimation error for spatially correlatedSpatial Correlation
Theoretically, the performance of wireless communication systems can be improved by having multiple antennas at the transmitter and the receiver. The idea is that if the propagation channels between each pair of transmit and receive antennas are statistically independent and identically...
channels can be minimized even if
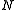is smaller than the number of transmit antennas. Thus, MMSE estimation can both decrease the estimation error and shorten the required training sequence. It needs however additionally the knowledge of the channel correlation matrix 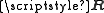and noise correlation matrix 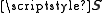. In absence of an accurate knowledge of these correlation matrices, robust choices need to be made to avoid MSE degradation.