This page covers applications of the Cartan formalism. For the general concept see Cartan connection

Cartan connection

In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...

.

The vierbein or tetrad

Tetrad

Tetrad may refer to:* Tetrad , Bivalents or Tetrad of homologous chromosomes consisting of four synapsed chromatids that become visible during the Pachytene stage of meiotic prophase...

theory much used in theoretical physics is a special case of the application of Cartan connection

Cartan connection

In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...

 in four-dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

s. It applies to metrics of any signature. (See Metric (mathematics)

Metric (mathematics)

In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...

.) This section is an approach to tetrads, but written in general terms. In dimensions other than 4, words like triad, pentad, zweibein, fünfbein, elfbein etc. have been used. Vielbein covers all dimensions. (In German, vier stands for four and viel stands for many.)

If you are looking for a basis-dependent index notation, see tetrad (index notation).

The basic ingredients

Suppose we are working on a differential manifold M of dimension n, and have fixed natural numbers p and q with

p + q = n.

Furthermore, we assume that we are given a SO(p, q) principal bundle

Principal bundle

In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...

 B over M and a SO(p, q)-vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

 V associated to B by means of the natural n-dimensional representation of SO(p, q). Equivalently, V is a rank n real vector bundle over M,
equiped with a metric

Metric (mathematics)

In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...

 η with signature

Metric signature

The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...

 (p, q) (aka non degenerate quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

).

The basic ingredient of the Cartan formalism is an invertible linear map 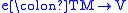, between vector bundle

Vector bundle

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...

s over M where TM is the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

 of M. The invertibility condition on e is sometimes dropped. In particular if B is the trivial bundle, as we can always assume locally,
V has a basis of orthogonal sections
. With respect to this basis
is a constant matrix. For a choice of local coordinates 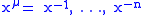on M (the negative indices are only to distinguish them from the indices labeling the 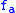) and a corresponding local frame
of the tangent bundle, the map e is determined by the images
of the basis sections
They determine a (non coordinate) basis of the tangent bundle (provided e is invertible and only locally if B is only locally trivialised). The matrix is called the tetrad, vierbein, vielbein etc.

Tetrad

Tetrad may refer to:* Tetrad , Bivalents or Tetrad of homologous chromosomes consisting of four synapsed chromatids that become visible during the Pachytene stage of meiotic prophase...

.
Its interpretation as a local frame crucially depends on the implicit choice of local bases.

Note that an isomorphism
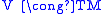gives a reduction  of the frame bundle

Frame bundle

In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...

, the principal bundle of the tangent bundle. In general, such a reduction is impossible for topological
reasons. Thus, in general for continuous maps e, one cannot avoid that e becomes degenerate at some points of M.

Example: general relativity

We can describe geometries in general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

 in terms of a tetrad field instead of the usual metric tensor field. The metric tensor 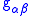gives the inner product in the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

 directly:


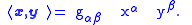
The tetrad may be seen as a (linear) map from the tangent space to Minkowski space which preserves the inner product. This lets us find the inner product in the tangent space by mapping our two vectors into Minkowski space and taking the usual inner product there: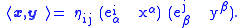


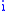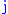Here and range over tangent-space coordinates, while and range over Minkowski coordinates. The tetrad field 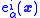defines a metric tensor field via the pullback .

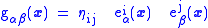Constructions

A (pseudo-

Pseudo-Riemannian manifold

In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...

)Riemannian metric is defined over M as the pullback of η by e. To put it in other words, if we have two sections of TM, X and Y,

g(X,Y) = η(e(X), e(Y)).

A connection

Connection form

In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....

 over V is defined as the unique connection A satisfying these two conditions:

• dη(a,b) = η(d_Aa,b) + η(a,d_Ab) for all differentiable sections a and b of V (i.e. d_Aη = 0) where d_A is the covariant exterior derivative. This implies that A can be extended to a connection
  Connection form
  In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
  
   over the SO(p,q) principal bundle
  Principal bundle
  In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
  
  .
• d_Ae = 0. The quantity on the left hand side is called the torsion
  Torsion
  The word torsion may refer to the following:*In geometry:** Torsion of a curve** Torsion tensor in differential geometry** The closely related concepts of Reidemeister torsion and analytic torsion ** Whitehead torsion*In algebra:** Torsion ** Tor functor* In medicine:** Ovarian...
  
  . This basically states that defined below is torsion-free. This condition is dropped in the Einstein-Cartan theory, but then we cannot define A uniquely anymore.

This is called the spin connection.

Now that we have specified A, we can use it to define a connection ∇ over TM via the isomorphism

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations.  If there exists an isomorphism between two structures, the two structures are said to be isomorphic.  In a certain sense, isomorphic structures are...

 e:

e(∇X) = d_Ae(X) for all differentiable sections X of TM.

Since what we now have here is a SO(p,q) gauge theory

Gauge theory

In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...

, the curvature F defined as 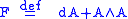is pointwise gauge covariant. This is simply the Riemann curvature tensor in a different form.

An alternate notation writes the connection form

Connection form

In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....

 A as ω, the curvature form

Curvature form

In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...

 F as Ω, the canonical vector-valued 1-form e as θ, and the exterior covariant derivative

Exterior covariant derivative

In mathematics, the exterior covariant derivative, sometimes also covariant exterior derivative, is a very useful notion for calculus on manifolds, which makes it possible to simplify formulas which use a principal connection....

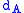  as D.

The Palatini action

In the tetrad formulation of general relativity, the action

Action (physics)

In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...

, as a functional

Functional (mathematics)

In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...

 of the cotetrad e and a connection form

Connection form

In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....

 A over a four-dimensional differential manifold M is given by


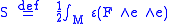
where F is the gauge curvature 2-form and ε is the antisymmetric intertwiner of four "vector" reps of SO(3,1) normalized by η.

Note that in the presence of spinor field

Spinor field

In particle physics, a spinor field of order 2s describes a particle of spin s, where s is an integer or half-integer. Therefore, a spinor of order 2s contains as much information as a tensor of order s...

s, the Palatini action implies that d_Ae is nonzero, that is, have torsion

Torsion

The word torsion may refer to the following:*In geometry:** Torsion of a curve** Torsion tensor in differential geometry** The closely related concepts of Reidemeister torsion and analytic torsion ** Whitehead torsion*In algebra:** Torsion ** Tor functor* In medicine:** Ovarian...

. See Einstein-Cartan theory.