Spinor field
Encyclopedia
In particle physics
, a spinor field of order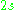
describes a particle of spin
, where 
is an integer or half-integer. Therefore, a spinor
of order
contains as much information as a tensor
of order
. As a result of this, particles of integer spin (bosons) can be described equally well by tensor field
s or spinor fields, whereas particles of half-integer spin (fermions) can be described only by spinor fields.
and possibly one of the neutrinos (a fermion).
If
is the spinor field describing a particle of spin s (where upper case Latin indices are spinor indices which can take the values 0 and 1), then it is symmetric and has 2s indices. If the particle is also of zero rest mass, then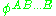 
satisfies the zero rest mass equation
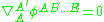
Here, in a Lorentz transformation
, primed spinors transform under the conjugate of the transformation for unprimed ones, Einstein summation is used throughout, and nabla denotes the spinor, which is equivalent to the Levi-Civita connection on Minkowski space
.
has one index for the neutrino, two for the photon, and four for the graviton. For the photon, the equation obtained states the vanishing of the divergence of the field strength tensor. For the graviton, it gives the Bianchi identity for a linearized Weyl tensor
.
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, a spinor field of order
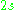describes a particle of spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, where is an integer or half-integer. Therefore, a spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
of order
contains as much information as a tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
of order
. As a result of this, particles of integer spin (bosons) can be described equally well by tensor fieldTensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
s or spinor fields, whereas particles of half-integer spin (fermions) can be described only by spinor fields.
Zero rest mass equation
Spinor fields describing particles of zero rest mass satisfy the so-called zero rest mass equation. Examples of zero rest mass particles include the gauge bosons (as long as gauge symmetry is not violated) such as the photonPhoton
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
and possibly one of the neutrinos (a fermion).
If
is the spinor field describing a particle of spin s (where upper case Latin indices are spinor indices which can take the values 0 and 1), then it is symmetric and has 2s indices. If the particle is also of zero rest mass, then 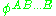satisfies the zero rest mass equation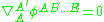Here, in a Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
, primed spinors transform under the conjugate of the transformation for unprimed ones, Einstein summation is used throughout, and nabla denotes the spinor, which is equivalent to the Levi-Civita connection on Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
has one index for the neutrino, two for the photon, and four for the graviton. For the photon, the equation obtained states the vanishing of the divergence of the field strength tensor. For the graviton, it gives the Bianchi identity for a linearized Weyl tensorWeyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
.
Further reading
- R. Sverdlov; A Geometrical Description of Spinor Fields; arXiv:0802.1914