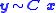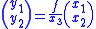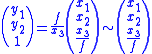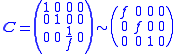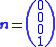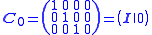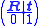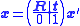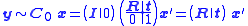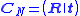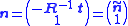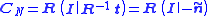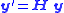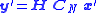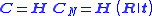Camera matrix
Encyclopedia
In computer vision
a camera matrix or (camera) projection matrix is a
matrix
which describes the mapping of a pinhole camera
from 3D points in the world to 2D points in an image.
Let
be a representation of a 3D point in homogeneous coordinates
(a 4-dimensional vector), and let
be a representation of the image of this point in the pinhole camera (a 3-dimensional vector). Then the following relation holds
where
is the camera matrix and the 
sign implies that the left and right hand sides are equal up to a non-zero scalar multiplication.
Since the camera matrix
is involved in the mapping between elements of two projective space
s, it too can be regarded as a projective element. This means that it has only 11 degrees of freedom since any multiplication by a non-zero scalar results in an equivalent camera matrix.
is given by
where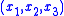
are the 3D coordinates of P relative to a camera centered coordinate system, 
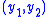are the resulting image coordinates, and f is the camera's focal length for which we assume f > 0. Furthermore, we also assume that x3 > 0.
To derive the camera matrix this expression is rewritten in terms of homogeneous coordinates. Instead of the 2D vector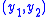
we consider the projective element (a 3D vector) 
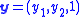and instead of equality we consider equality up to scaling by a non-zero number, denoted 
. First, we write the homogeneous image coordinates as expressions in the usual 3D coordinates.
Finally, also the 3D coordinates are expressed in a homogeneous representation
and this is how the camera matrix appears:
where
is the camera matrix, which here is given by
and the corresponding camera matrix now becomes
The last step is a consequence of
itself being a projective element.
The camera matrix derived here may appear trivial in the sense that it contains very few non-zero elements. This depends to a large extent on the particular coordinate systems which have been chosen for the 3D and 2D points. In practice, however, other forms of camera matrices are common, as will be shown below.
derived in the previous section has a null space
which is spanned by the vector
This is also the homogeneous representation of the 3D point which has coordinates (0,0,0), that is, the camera focal point O. This means that the focal point (and only this point) cannot be mapped to a particular point in the image plane by the camera. This is consistent with the fact that the projection line becomes ambiguous in this case.
where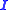
here denotes a 
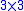identity matrix. Note that 
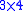matrix 
here is divided into a concatenation of a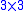 
matrix and a 3-dimensional vector. The camera matrix 
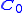is sometimes referred to as a canonical form.
So far all points in the 3D world have been represented in a camera centered coordinate system, that is, a coordinate system which has its origin at the camera focal point. In practice however, the 3D points may be represented in terms of coordinates relative to an arbitrary coordinate system (X1',X2',X3'). Assuming that the camera coordinate axes (X1,X2,X3) and the axes (X1',X2',X3') are of Euclidean type (orthogonal and isotropic), there is a unique Euclidean 3D transformation (rotation and translation) between the two coordinate systems.
The two operations of rotation and translation of 3D coordinates can be represented as the two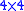
matrices
where
is a 
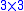rotation matrix and 
is a 3-dimensional translation vector. When the first matrix is multiplied onto the homogeneous representation of a 3D point, the result is the homogeneous representation of the rotated point, and the second matrix performs instead a translation. Performing the two operations in sequence gives a combined rotation and translation matrix
Assuming that
and 
are precisely the rotation and translations which relate the two coordinate system (X1,X2,X3) and (X1',X2',X3') above, this implies that
where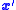
is the homogeneous representation of the point P in the coordinate system (X1',X2',X3').
Assuming also that the camera matrix is given by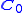
, the mapping from the coordinates in the (X1',X2',X3') system to homogeneous image coordinates becomes
Consequently, the camera matrix which relates points in the coordinate system (X1',X2',X3') to image coordinates is
a concatenation of a 3D rotation matrix and a 3-dimensional translation vector.
This type of camera matrix is referred to as a normalized camera matrix, it assumes focal length = 1 and that image coordinates are measured in a coordinate system where the origin is located at the intersection between axis X3 and the image plane and has the same units as the 3D coordinate system. The resulting image coordinates are referred to as normalized image coordinates.
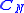described above is spanned by the 4-dimensional vector
This is also, again, the coordinates of the focal point but now relative to the (X1',X2',X3') system. This can be seen by applying first the rotation and then the translation to the 3-dimensional vector
and the result is the homogeneous representation of 3D coordinates (0,0,0).
This implies that the focal point (in its homogeneous representation) lies in the null space of the camera matrix, provided that it is represented in terms of 3D coordinates relative to the same coordinate system as the camera matrix refers to.
The normalized camera matrix
can now be written as
where
is the 3D coordinates of the focal point relative to the (X1',X2',X3') system.
. This includes 2D translations and rotations as well as scaling (isotropic and anisotropic) but also general 2D perspective transformations. Such a transformation can be represented as a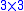
matrix 
which maps the homogeneous normalized image coordinates 
to the homogeneous transformed image coordinates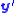 
:
Inserting the above expression for the normalized image coordinates in terms of the 3D coordinates gives
This produces the most general form of camera matrix
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
a camera matrix or (camera) projection matrix is a
matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which describes the mapping of a pinhole camera
Pinhole camera
A pinhole camera is a simple camera without a lens and with a single small aperture – effectively a light-proof box with a small hole in one side. Light from a scene passes through this single point and projects an inverted image on the opposite side of the box...
from 3D points in the world to 2D points in an image.
Let
be a representation of a 3D point in homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
(a 4-dimensional vector), and let
be a representation of the image of this point in the pinhole camera (a 3-dimensional vector). Then the following relation holds
where
is the camera matrix and the sign implies that the left and right hand sides are equal up to a non-zero scalar multiplication.Since the camera matrix
is involved in the mapping between elements of two projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s, it too can be regarded as a projective element. This means that it has only 11 degrees of freedom since any multiplication by a non-zero scalar results in an equivalent camera matrix.
Derivation
The mapping from the coordinates of a 3D point P to the 2D image coordinates of the point's projection onto the image plane, according to the pinhole camera modelPinhole camera model
The pinhole camera model describes the mathematical relationship between the coordinates of a 3D point and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light...
is given by
where
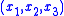are the 3D coordinates of P relative to a camera centered coordinate system, 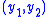are the resulting image coordinates, and f is the camera's focal length for which we assume f > 0. Furthermore, we also assume that x3 > 0.To derive the camera matrix this expression is rewritten in terms of homogeneous coordinates. Instead of the 2D vector
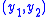we consider the projective element (a 3D vector) 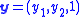and instead of equality we consider equality up to scaling by a non-zero number, denoted . First, we write the homogeneous image coordinates as expressions in the usual 3D coordinates.
Finally, also the 3D coordinates are expressed in a homogeneous representation
and this is how the camera matrix appears:-
or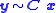 
where
is the camera matrix, which here is given by-
,
and the corresponding camera matrix now becomes
The last step is a consequence of
itself being a projective element.The camera matrix derived here may appear trivial in the sense that it contains very few non-zero elements. This depends to a large extent on the particular coordinate systems which have been chosen for the 3D and 2D points. In practice, however, other forms of camera matrices are common, as will be shown below.
The camera focal point
The camera matrix derived in the previous section has a null spaceNull space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
which is spanned by the vector
This is also the homogeneous representation of the 3D point which has coordinates (0,0,0), that is, the camera focal point O. This means that the focal point (and only this point) cannot be mapped to a particular point in the image plane by the camera. This is consistent with the fact that the projection line becomes ambiguous in this case.
Normalized camera matrix and normalized image coordinates
The camera matrix derived above can be simplified even further if we assume that f = 1:
where
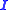here denotes a 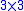identity matrix. Note that 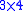matrix here is divided into a concatenation of a 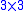matrix and a 3-dimensional vector. The camera matrix 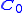is sometimes referred to as a canonical form.So far all points in the 3D world have been represented in a camera centered coordinate system, that is, a coordinate system which has its origin at the camera focal point. In practice however, the 3D points may be represented in terms of coordinates relative to an arbitrary coordinate system (X1',X2',X3'). Assuming that the camera coordinate axes (X1,X2,X3) and the axes (X1',X2',X3') are of Euclidean type (orthogonal and isotropic), there is a unique Euclidean 3D transformation (rotation and translation) between the two coordinate systems.
The two operations of rotation and translation of 3D coordinates can be represented as the two
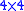matrices-
and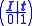 
where
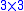is a rotation matrix and is a 3-dimensional translation vector. When the first matrix is multiplied onto the homogeneous representation of a 3D point, the result is the homogeneous representation of the rotated point, and the second matrix performs instead a translation. Performing the two operations in sequence gives a combined rotation and translation matrix
Assuming that
and are precisely the rotation and translations which relate the two coordinate system (X1,X2,X3) and (X1',X2',X3') above, this implies that
where
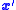is the homogeneous representation of the point P in the coordinate system (X1',X2',X3').Assuming also that the camera matrix is given by
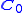, the mapping from the coordinates in the (X1',X2',X3') system to homogeneous image coordinates becomes
Consequently, the camera matrix which relates points in the coordinate system (X1',X2',X3') to image coordinates is
a concatenation of a 3D rotation matrix and a 3-dimensional translation vector.
This type of camera matrix is referred to as a normalized camera matrix, it assumes focal length = 1 and that image coordinates are measured in a coordinate system where the origin is located at the intersection between axis X3 and the image plane and has the same units as the 3D coordinate system. The resulting image coordinates are referred to as normalized image coordinates.
The camera focal point
The null space of the normalized camera matrix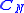 described above is spanned by the 4-dimensional vector
This is also, again, the coordinates of the focal point but now relative to the (X1',X2',X3') system. This can be seen by applying first the rotation and then the translation to the 3-dimensional vector
and the result is the homogeneous representation of 3D coordinates (0,0,0).This implies that the focal point (in its homogeneous representation) lies in the null space of the camera matrix, provided that it is represented in terms of 3D coordinates relative to the same coordinate system as the camera matrix refers to.
The normalized camera matrix
can now be written as
where
is the 3D coordinates of the focal point relative to the (X1',X2',X3') system.General camera matrix
Given the mapping produced by a normalized camera matrix, the resulting normalized image coordinates can be transformed by means of an arbitrary 2D homographyHomography
Homography is a concept in the mathematical science of geometry.A homography is an invertible transformation from a projective space to itself that maps straight lines to straight lines...
. This includes 2D translations and rotations as well as scaling (isotropic and anisotropic) but also general 2D perspective transformations. Such a transformation can be represented as a
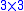matrix which maps the homogeneous normalized image coordinates to the homogeneous transformed image coordinates :
Inserting the above expression for the normalized image coordinates in terms of the 3D coordinates gives
This produces the most general form of camera matrix
