Bromwich integral
Encyclopedia
Mellin's inverse formula
An integral formula for the inverse Laplace transform, called the Bromwich integral, the Fourier–Mellin integral, and Mellin's inverse formula, is given by the line integralLine integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
:
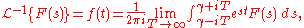
where the integration is done along the vertical line
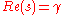in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
such that
is greater than the real part of all singularitiesMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
of F(s). This ensures that the contour path is in the region of convergence.
If all singularities are in the left half-plane, or F(s) is a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
on - ∞ < Re(s) < ∞ (i.e. no singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
), then
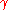can be set to zero and the above inverse integral formula above becomes identical to the inverse Fourier transform.In practice, computing the complex integral can be done by using the Cauchy residue theorem.
It is named after Hjalmar Mellin
Hjalmar Mellin
Robert Hjalmar Mellin was a Finnish mathematician and functional theorist.He studied at the University of Helsinki and later in Berlin under Karl Weierstrass. He is most noted as the developer of the integral transform known as the Mellin transform...
, Joseph Fourier
Joseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
and Thomas John I'Anson Bromwich
Thomas John I'Anson Bromwich
Thomas John I'Anson Bromwich was an English mathematician, and a Fellow of the Royal Society. His third name begins with an uppercase i, as opposed to the lowercase L which would seem more likely.-Life:...
.
Post's inversion formula
An alternative formula for the inverse Laplace transform is given by Post's inversion formulaPost's inversion formula
Post's inversion formula for Laplace transforms, named after Emil Post, is a simple-looking but usually impractical formula for evaluating an inverse Laplace transform....
.
External links
- Tables of Integral Transforms at EqWorld: The World of Mathematical Equations.