Bernstein's theorem
Encyclopedia
In real analysis
, a branch of mathematics
, Bernstein's theorem states that any real-valued
function on the half-line[ 0, ∞) that is totally monotone is a mixture of exponential functions. In one important special case the mixture is a weighted average, or expected value
.
Total monotonicity (sometimes also complete monotonicity) of a function f means that f is continuous on[ 0, ∞) , infinitely differentiable on
( 0, ∞) , and satisfies
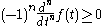
for all nonnegative integers n and for all t > 0. Another convention puts the opposite inequality in the above definition.
The "weighted average" statement can be characterized thus: there is a non-negative finite Borel measure on[ 0, ∞) , with cumulative distribution function
g, such that
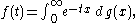
the integral being a Riemann–Stieltjes integral.
Nonnegative functions whose derivative is completely monotone are called Bernstein functions. Any Bernstein function can be written in the following form:
where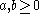
and 
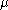is a measure on the positive real half-line such that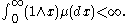
In more abstract language, the theorem characterises Laplace transforms of positive Borel measures on [0,∞). In this form it is known as the Bernstein–Widder theorem, or Hausdorff–Bernstein–Widder theorem. Felix Hausdorff
had earlier characterised completely monotone sequences. These are the sequences occurring in the Hausdorff moment problem.
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Bernstein's theorem states that any real-valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
function on the half-line
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
.
Total monotonicity (sometimes also complete monotonicity) of a function f means that f is continuous on
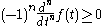
for all nonnegative integers n and for all t > 0. Another convention puts the opposite inequality in the above definition.
The "weighted average" statement can be characterized thus: there is a non-negative finite Borel measure on
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
g, such that
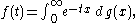
the integral being a Riemann–Stieltjes integral.
Nonnegative functions whose derivative is completely monotone are called Bernstein functions. Any Bernstein function can be written in the following form:
where
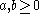and 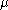is a measure on the positive real half-line such that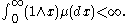In more abstract language, the theorem characterises Laplace transforms of positive Borel measures on [0,∞). In this form it is known as the Bernstein–Widder theorem, or Hausdorff–Bernstein–Widder theorem. Felix Hausdorff
Felix Hausdorff
Felix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
had earlier characterised completely monotone sequences. These are the sequences occurring in the Hausdorff moment problem.