
Bernoulli polynomials
Encyclopedia
In mathematics
, the Bernoulli polynomials occur in the study of many special functions
and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative
operator. Unlike orthogonal polynomials
, the Bernoulli polynomials are remarkable in that the number of crossings of the x-axis in the unit interval
does not go up as the degree of the polynomials goes up. In the limit of large degree, the Bernoulli polynomials, appropriately scaled, approach the sine and cosine functions
.

. Which among them should be taken to be the definition may depend on one's purposes.
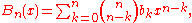
for n ≥ 0, where bk are the Bernoulli number
s.
for the Bernoulli polynomials is
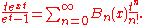
The generating function for the Euler polynomials is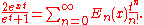
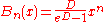
where D = d/dx is differentiation with respect to x and the fraction is expanded as a formal power series
.
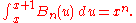
The integral operator
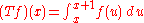
on polynomials f, is the same as
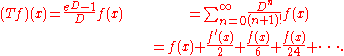
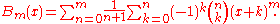
Note the remarkable similarity to the globally convergent series expression for the Hurwitz zeta function. Indeed, one has
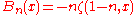
where ζ(s, q) is the Hurwitz zeta; thus, in a certain sense, the Hurwitz zeta generalizes the Bernoulli polynomials to non-integer values of n.
The inner sum may be understood to be the nth forward difference of xm; that is,
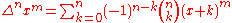
where Δ is the forward difference operator. Thus, one may write

This formula may be derived from an identity appearing above as follows: since the forward difference operator Δ is equal to
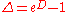
where D is differentiation with respect to x, we have
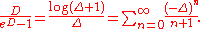
As long as this operates on an mth-degree polynomial such as xm, one may let n go from 0 only up to m.
An integral representation for the Bernoulli polynomials is given by the Nörlund–Rice integral, which follows from the expression as a finite difference.
An explicit formula for the Euler polynomials is given by
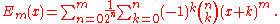
This may also be written in terms of the Euler numbers Ek as
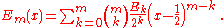

See Faulhaber's formula for more on this.
s are given by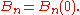
An alternate convention defines the Bernoulli numbers as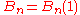 . This definition gives Bn = −nζ(1 − n) where for n = 0 and n = 1 the expression −nζ(1 − n) is to be understood as
. This definition gives Bn = −nζ(1 − n) where for n = 0 and n = 1 the expression −nζ(1 − n) is to be understood as
limx → n −xζ(1 − x).
The two conventions differ only for n = 1 since B1(1) = 1/2 = −B1(0).
The Euler numbers are given by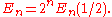


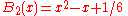
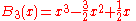
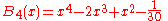

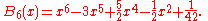
The first few Euler polynomials are

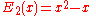
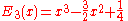
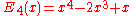
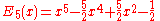
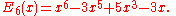
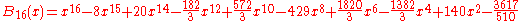
which shows that the value at x = 0 (and at x = 1) is −3617/510 ≈ −7.09, while at x = 1/2, the value is 118518239/3342336 ≈ +7.09. D.H. Lehmer showed that the maximum value of Bn(x) between 0 and 1 obeys
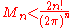
unless n is 2 modulo 4, in which case
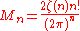
(where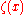 is the Riemann zeta function), while the minimum obeys
is the Riemann zeta function), while the minimum obeys
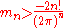
unless n is 0 modulo 4, in which case
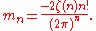
These limits are quite close to the actual maximum and minimum, and Lehmer gives more accurate limits as well.
:
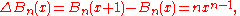
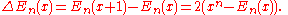
(Δ is the forward difference operator).
These polynomial sequence
s are Appell sequences:

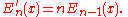
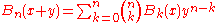
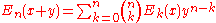
These identities are also equivalent to saying that these polynomial sequences are Appell sequences. (Hermite polynomials
are another example.)
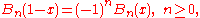
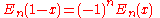
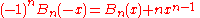
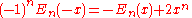
Zhi-Wei Sun
and Hao Pan established the following surprising symmetric relation: If r + s + t = n and x + y + z = 1, then
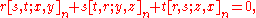
where
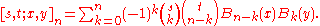
of the Bernoulli polynomials is also a Dirichlet series, given by the expansion
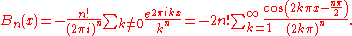
This is a special case of the analogous form for the Hurwitz zeta function

This expansion is valid only for 0 ≤ x ≤ 1 when n ≥ 2 and is valid for 0 < x < 1 when n = 1.
The Fourier series of the Euler polynomials may also be calculated. Defining the functions
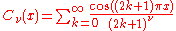
and

for , the Euler polynomial has the Fourier series
, the Euler polynomial has the Fourier series
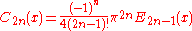
and
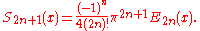
Note that the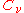 and
and 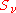 are odd and even, respectively:
are odd and even, respectively:

and
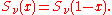
They are related to the Legendre chi function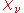 as
as
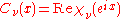
and

in terms of the polynomials. Specifically, one has
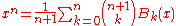
and
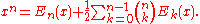
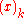 as
as
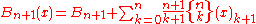
where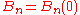 and
and
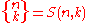
denotes the Stirling number of the second kind. The above may be inverted to express the falling factorial in terms of the Bernoulli polynomials:
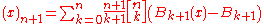
where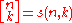
denotes the Stirling number of the first kind.
s were given by Joseph Ludwig Raabe
in 1851:
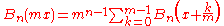
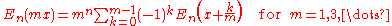

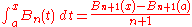
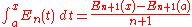
Definite integrals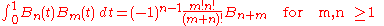
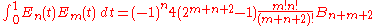
of the argument x. These functions are used to provide the remainder term in the Euler–Maclaurin formula relating sums to integrals. The first polynomial is a sawtooth function
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bernoulli polynomials occur in the study of many special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
operator. Unlike orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
, the Bernoulli polynomials are remarkable in that the number of crossings of the x-axis in the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
does not go up as the degree of the polynomials goes up. In the limit of large degree, the Bernoulli polynomials, appropriately scaled, approach the sine and cosine functions
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
.

Representations
The Bernoulli polynomials Bn admit a variety of different representationsRepresentation (mathematics)
In mathematics, representation is a very general relationship that expresses similarities between objects. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the...
. Which among them should be taken to be the definition may depend on one's purposes.
Explicit formula
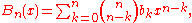
for n ≥ 0, where bk are the Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s.
Generating functions
The generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the Bernoulli polynomials is
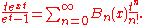
The generating function for the Euler polynomials is
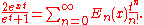
Representation by a differential operator
The Bernoulli polynomials are also given by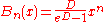
where D = d/dx is differentiation with respect to x and the fraction is expanded as a formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
.
Representation by an integral operator
The Bernoulli polynomials are the unique polynomials determined by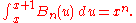
The integral operator
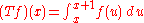
on polynomials f, is the same as
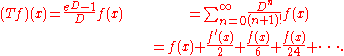
Another explicit formula
An explicit formula for the Bernoulli polynomials is given by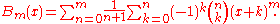
Note the remarkable similarity to the globally convergent series expression for the Hurwitz zeta function. Indeed, one has
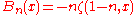
where ζ(s, q) is the Hurwitz zeta; thus, in a certain sense, the Hurwitz zeta generalizes the Bernoulli polynomials to non-integer values of n.
The inner sum may be understood to be the nth forward difference of xm; that is,
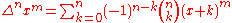
where Δ is the forward difference operator. Thus, one may write

This formula may be derived from an identity appearing above as follows: since the forward difference operator Δ is equal to
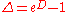
where D is differentiation with respect to x, we have
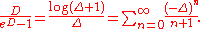
As long as this operates on an mth-degree polynomial such as xm, one may let n go from 0 only up to m.
An integral representation for the Bernoulli polynomials is given by the Nörlund–Rice integral, which follows from the expression as a finite difference.
An explicit formula for the Euler polynomials is given by
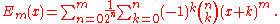
This may also be written in terms of the Euler numbers Ek as
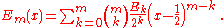
Sums of pth powers
We have
See Faulhaber's formula for more on this.
The Bernoulli and Euler numbers
The Bernoulli numberBernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s are given by
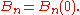
An alternate convention defines the Bernoulli numbers as
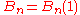 . This definition gives Bn = −nζ(1 − n) where for n = 0 and n = 1 the expression −nζ(1 − n) is to be understood as
. This definition gives Bn = −nζ(1 − n) where for n = 0 and n = 1 the expression −nζ(1 − n) is to be understood aslimx → n −xζ(1 − x).
The two conventions differ only for n = 1 since B1(1) = 1/2 = −B1(0).
The Euler numbers are given by
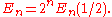
Explicit expressions for low degrees
The first few Bernoulli polynomials are:

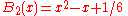
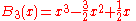
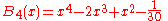

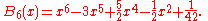
The first few Euler polynomials are


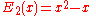
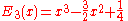
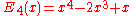
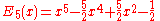
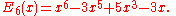
Maximum and minimum
At higher n, the amount of variation in Bn(x) between x = 0 and x = 1 gets large. For instance,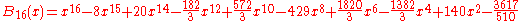
which shows that the value at x = 0 (and at x = 1) is −3617/510 ≈ −7.09, while at x = 1/2, the value is 118518239/3342336 ≈ +7.09. D.H. Lehmer showed that the maximum value of Bn(x) between 0 and 1 obeys
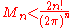
unless n is 2 modulo 4, in which case
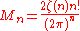
(where
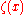 is the Riemann zeta function), while the minimum obeys
is the Riemann zeta function), while the minimum obeys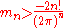
unless n is 0 modulo 4, in which case
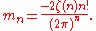
These limits are quite close to the actual maximum and minimum, and Lehmer gives more accurate limits as well.
Differences and derivatives
The Bernoulli and Euler polynomials obey many relations from umbral calculusUmbral calculus
In mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
:
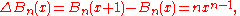
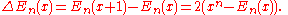
(Δ is the forward difference operator).
These polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
s are Appell sequences:

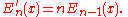
Translations
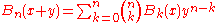
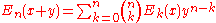
These identities are also equivalent to saying that these polynomial sequences are Appell sequences. (Hermite polynomials
Hermite polynomials
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
are another example.)
Symmetries
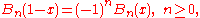
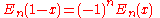
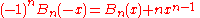
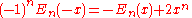
Zhi-Wei Sun
Zhi-Wei Sun
Zhi-Wei Sun is a Chinese mathematician, working primarily on number theory, combinatorics, and group theory. Currently he works as a professor in Nanjing University....
and Hao Pan established the following surprising symmetric relation: If r + s + t = n and x + y + z = 1, then
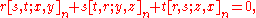
where
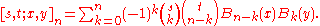
Fourier series
The Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of the Bernoulli polynomials is also a Dirichlet series, given by the expansion
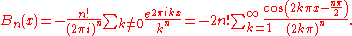
This is a special case of the analogous form for the Hurwitz zeta function

This expansion is valid only for 0 ≤ x ≤ 1 when n ≥ 2 and is valid for 0 < x < 1 when n = 1.
The Fourier series of the Euler polynomials may also be calculated. Defining the functions
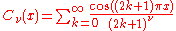
and

for
 , the Euler polynomial has the Fourier series
, the Euler polynomial has the Fourier series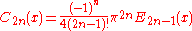
and
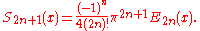
Note that the
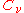 and
and 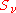 are odd and even, respectively:
are odd and even, respectively:
and
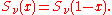
They are related to the Legendre chi function
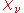 as
as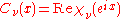
and

Inversion
The Bernoulli and Euler polynomials may be inverted to express the monomialMonomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
in terms of the polynomials. Specifically, one has
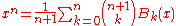
and
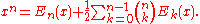
Relation to falling factorial
The Bernoulli polynomials may be expanded in terms of the falling factorial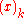 as
as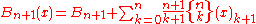
where
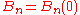 and
and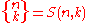
denotes the Stirling number of the second kind. The above may be inverted to express the falling factorial in terms of the Bernoulli polynomials:
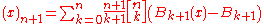
where
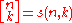
denotes the Stirling number of the first kind.
Multiplication theorems
The multiplication theoremMultiplication theorem
In mathematics, the multiplication theorem is a certain type of identity obeyed by many special functions related to the gamma function. For the explicit case of the gamma function, the identity is a product of values; thus the name...
s were given by Joseph Ludwig Raabe
Joseph Ludwig Raabe
Joseph Ludwig Raabe was a Swiss mathematician.-Life:As his parents were quite poor, Raabe was forced to earn his living from a very early age by giving private lessons. He began to study mathematics in 1820 at the Polytechnicum in Vienna, Austria...
in 1851:
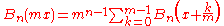
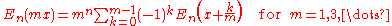

Integrals
Indefinite integrals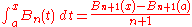
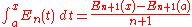
Definite integrals
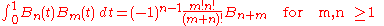
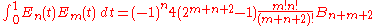
Periodic Bernoulli polynomials
A periodic Bernoulli polynomial Pn(x) is a Bernoulli polynomial evaluated at the fractional partFractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
of the argument x. These functions are used to provide the remainder term in the Euler–Maclaurin formula relating sums to integrals. The first polynomial is a sawtooth function
Sawtooth wave
The sawtooth wave is a kind of non-sinusoidal waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw....
.

