Baum–Connes conjecture
Encyclopedia
In mathematics
, specifically in operator K-theory
, the Baum–Connes conjecture suggests a link between the K-theory
of the C*-algebra of a group
and the K-homology
of the corresponding classifying space of proper actions of that group.
It thus sets up a correspondence between different areas of mathematics, the K-homology being related to geometry, differential operator theory, and homotopy theory, while the K-theory of the reduced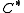
-algebra is a purely analytical object.
The conjecture, if true, would have some older famous conjectures as consequences. For instance, the surjectivity part implies the Kadison-Kaplansky conjecture
for a discrete torsion-free group, and the injectivity is closely related to the Novikov conjecture
.
The conjecture is also closely related to index theory, as the assembly map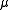
is a sort of index, and it plays a major role in Alain Connes
' noncommutative geometry
program.
The origins of the conjecture go back to Fredholm theory
, the Atiyah-Singer index theorem and the interplay of geometry with operator K-theory as expressed in the works of Brown, Douglas and Fillmore, among many other motivating subjects.
locally compact group
(for instance a countable discrete group
). One can define a morphism
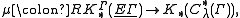
called the assembly map, from the equivariant K-homology with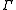
-compact supports of the classifying space of proper actions 
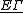to the K-theory of the reduced C*-algebra of Γ. The index * can be 0 or 1.
Paul Baum and Alain Connes
introduced the following conjecture (1982) about this morphism:
As the left hand side tends to be more easily accessible than the right hand side, because there are hardly any general structure theorems of the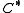
-algebra, one usually views the conjecture as an "explanation" of the right hand side.
The original formulation of the conjecture was somewhat different, as the notion of equivariant K-homology was not yet common in 1982.
In case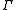
is discrete and torsion-free, the left hand side reduces to the non-equivariant K-homology with compact supports of the ordinary classifying space 
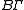of 
.
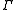There is also more general form of the conjecture, known as Baum-Connes conjecture with coefficients, where both sides have coefficients in the form of a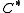
-algebra 
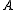on which 
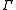acts by 
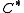-automorphisms. It says in KK-language that the assembly map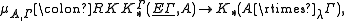
is an isomorphism, containing the case without coefficients as the case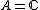
.
However, counterexamples to the conjecture with coefficients were found in 2002 by Nigel Higson, Vincent Lafforgue
and George Skandalis, basing on not universally accepted, as of 2008, results of Gromov on expanders in Cayley graphs. Even provided validity of Higson, Lafforgue & Skandalis, conjecture with coefficients remains an active area of research, since it is, not unlike the classical conjecture, often seen as a statement concerning particular groups or class of groups.
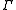be the integers 
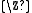. Then the left hand side is the K-homology
of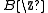
which is the circle. The 
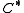-algebra of the integers is by the commutative Gelfand-Naimark-transform, which reduces to the Fourier transform
in this case, isomorphic to the algebra of continuous functions on the circle. So the right hand side is the topological K-theory of the circle. One can then show that the assembly map is KK-theoretic Poincaré duality
as defined by Guennadi Kasparov, which is an isomorphism.
Another simple example is given by compact groups. In this case, both sides identify naturally with the complex representation ring
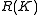of the group in such a way that the assembly map becomes the identity.
The conjecture is proved for the following classes of groups:
Injectivity is known for a much larger class of groups thanks to the Dirac-dual-Dirac method. This goes back to ideas of Michael Atiyah
and was developed in great generality by Gennadi Kasparov in 1987.
Injectivity is known for the following classes:
The simplest example of a group for which it is not known whether it satisfies the conjecture is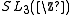
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in operator K-theory
Operator K-theory
In mathematics, operator K-theory is a variant of K-theory on the category of Banach algebras ....
, the Baum–Connes conjecture suggests a link between the K-theory
Operator K-theory
In mathematics, operator K-theory is a variant of K-theory on the category of Banach algebras ....
of the C*-algebra of a group
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and the K-homology
K-homology
In mathematics, K-homology is a homology theory on the category of compact Hausdorff spaces. It classifies the elliptic pseudo-differential operators acting on the vector bundles over a space...
of the corresponding classifying space of proper actions of that group.
It thus sets up a correspondence between different areas of mathematics, the K-homology being related to geometry, differential operator theory, and homotopy theory, while the K-theory of the reduced
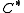-algebra is a purely analytical object.The conjecture, if true, would have some older famous conjectures as consequences. For instance, the surjectivity part implies the Kadison-Kaplansky conjecture
Kaplansky conjecture
The mathematician Irving Kaplansky is notable for proposing numerous conjectures in several branches of mathematics, including a list of ten conjectures on Hopf algebras...
for a discrete torsion-free group, and the injectivity is closely related to the Novikov conjecture
Novikov conjecture
The Novikov conjecture is one of the most important unsolved problems in topology. It is named for Sergei Novikov who originally posed the conjecture in 1965....
.
The conjecture is also closely related to index theory, as the assembly map
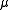is a sort of index, and it plays a major role in Alain ConnesAlain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
' noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
program.
The origins of the conjecture go back to Fredholm theory
Fredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
, the Atiyah-Singer index theorem and the interplay of geometry with operator K-theory as expressed in the works of Brown, Douglas and Fillmore, among many other motivating subjects.
Formulation
Let Γ be a second countableSecond-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
(for instance a countable discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
). One can define a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
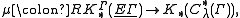
called the assembly map, from the equivariant K-homology with
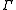-compact supports of the classifying space of proper actions 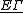to the K-theory of the reduced C*-algebra of Γ. The index * can be 0 or 1.Paul Baum and Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
introduced the following conjecture (1982) about this morphism:
- The assembly map μ is an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
As the left hand side tends to be more easily accessible than the right hand side, because there are hardly any general structure theorems of the
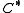-algebra, one usually views the conjecture as an "explanation" of the right hand side.The original formulation of the conjecture was somewhat different, as the notion of equivariant K-homology was not yet common in 1982.
In case
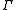is discrete and torsion-free, the left hand side reduces to the non-equivariant K-homology with compact supports of the ordinary classifying space 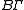of 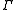.There is also more general form of the conjecture, known as Baum-Connes conjecture with coefficients, where both sides have coefficients in the form of a
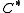-algebra 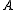on which 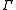acts by 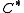-automorphisms. It says in KK-language that the assembly map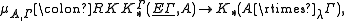is an isomorphism, containing the case without coefficients as the case
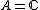.However, counterexamples to the conjecture with coefficients were found in 2002 by Nigel Higson, Vincent Lafforgue
Vincent Lafforgue
Vincent Lafforgue is a French mathematician. He is a "Directeur de Recherches" at the Université d'Orléans since September 1, 2010. Lafforgue was awarded the 2000 EMS Prize for his contribution to the K-theory of operator algebras: the proof of the Baum–Connes conjecture for discrete co-compact...
and George Skandalis, basing on not universally accepted, as of 2008, results of Gromov on expanders in Cayley graphs. Even provided validity of Higson, Lafforgue & Skandalis, conjecture with coefficients remains an active area of research, since it is, not unlike the classical conjecture, often seen as a statement concerning particular groups or class of groups.
Examples
Let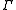 be the integers 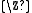. Then the left hand side is the K-homologyK-homology
In mathematics, K-homology is a homology theory on the category of compact Hausdorff spaces. It classifies the elliptic pseudo-differential operators acting on the vector bundles over a space...
of
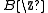which is the circle. The 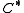-algebra of the integers is by the commutative Gelfand-Naimark-transform, which reduces to the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
in this case, isomorphic to the algebra of continuous functions on the circle. So the right hand side is the topological K-theory of the circle. One can then show that the assembly map is KK-theoretic Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
as defined by Guennadi Kasparov, which is an isomorphism.
Another simple example is given by compact groups. In this case, both sides identify naturally with the complex representation ring
Representation ring
In mathematics, especially in the area of algebra known as representation theory, the representation ring of a group is a ring formed from all the linear representations of the group. For a given group, the ring will depend on the base field of the representations...
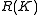of the group in such a way that the assembly map becomes the identity.Results
The conjecture without coefficients is still open, although the field has received great attention since 1982.The conjecture is proved for the following classes of groups:
- Discrete subgroups of
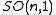and 
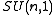. - Groups with the Haagerup propertyHaagerup propertyIn mathematics, the Haagerup property, also known as Gromov's a-T-menability, is a property of groups that is a strong negation of Kazhdan's property...
, sometimes called a-T-menable groups. These are groups that admit an isometric action on an affine Hilbert space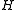
which is proper in the sense that 
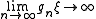for all 
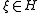and all sequences of group elements 
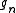with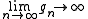 
. Examples of a-T-menable groups are amenable groupsAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
, Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s, groups acting properly on trees, and groups acting properly on simply connected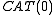
cubical complexes. - Groups that admit a finite presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
with only one relation. - Discrete cocompact subgroups of real Lie groups of real rank 1.
- Cocompact lattices in
,
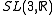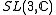or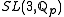 
. It was a long-standing problem since the first days of the conjecture to expose a single infinite property T-group that satisfies it. However, such a group was given by V. Lafforgue in 1998 as he showed that cocompact lattices in 
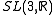have the property of rapid decay and thus satisfy the conjecture. - Gromov hyperbolic groupsHyperbolic groupIn group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
and their subgroups. - Among non-discrete groups, the conjecture has been shown in 2003 by J. Chabert, S. Echterhoff and R. Nest for the vast class of all almost connected groups (i. e. groups having a cocompact connected component), and all groups of
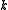-rational points of a linear algebraic groupLinear algebraic groupIn mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
over a local fieldLocal fieldIn mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
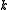of characteristic zero (e.g. 
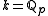). For the important subclass of real reductive groups, the conjecture had already been shown in 1982 by A. Wassermann.
Injectivity is known for a much larger class of groups thanks to the Dirac-dual-Dirac method. This goes back to ideas of Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
and was developed in great generality by Gennadi Kasparov in 1987.
Injectivity is known for the following classes:
- Discrete subgroups of connected Lie groups or virtually connected Lie groups.
- Discrete subgroups of p-adic groupsP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
. - Bolic groups (a certain generalization of hyperbolic groups).
- Groups which admit an amenable action on some compact space.
The simplest example of a group for which it is not known whether it satisfies the conjecture is
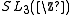.External links
- On the Baum-Connes conjecture by Dmitry Matsnev.