Operator K-theory
Encyclopedia
In mathematics
, operator K-theory is a variant of K-theory
on the category
of Banach algebras (In most applications, these Banach algebras are C*-algebras).
Its basic feature that distinguishes it from algebraic K-theory
is that it has a Bott periodicity. So there are only two K-groups, namely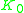
, equal to algebraic 
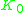, and 
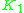. As a consequence of the periodicity theorem, it satisfies excision
. This means that it associates to an extension of C*-algebras to a long exact sequence, which, by Bott periodicity, reduces to an exact cyclic 6-term-sequence.
Operator K-theory is a generalization of topological K-theory
, defined by means of vector bundle
s on locally compact Hausdorff space
s. Here, an n-dimensional vector bundle over a topological space X is associated to a projection in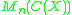
, where 
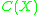is the C* algebra of continuous functions over X. Also, it is known that homotopy equivalence of vector bundles translates to Murray-von Neumann equivalence of the associated projection in K⊗
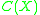, where K is compact operators on a separable Hilbert space.
Hence, the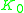
group of a (not necessarily commutative) C* algebra A is defined as Grothendieck group
generated by the Murray-von Neumann equivalence classes of projections in K⊗
. 
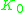is a functor from the category of C* Algebras and *-homomorphisms, to the category of abelian groups and group homomorphisms. The higher K-functors are defined via a C*-version of the suspension:
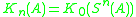where
However, by Bott periodicity, it turns out that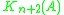
and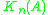 
are isomorphic for each n, and thus the only groups produced by this construction are 
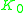and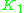 
.
The key reason for the introduction of K-theoretic methods into the study of C*-algebras was the Fredholm index: Given a bounded linear operator on a Hilbert space that has finite dimensional kernel and co-kernel, one can associate to it an integer, which, as it turns out, reflects the 'defect' on the operator - i.e. the extent to which it is not invertible. In analysis on manifolds, this index and its generalizations played a crucial role in the index theory of Atiyah and Singer, where the topological index of the manifold can be expressed via the index of elliptic operators on it. Later on, Brown, Douglas and Fillmore observed that the Fredholm index was the missing ingredient in classifying essentially normal operators up to certain natural equivalence. These ideas, together with Elliott's classification of AF C*-algebras via K-theory led to a great deal of interest in adapting methods such as K-theory from algebraic topology into the study of operator algebras.
This, in turn, led to K-homology
, Kasparov's bivariant KK-Theory
, and, more recently, Connes
and Higson's E-theory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, operator K-theory is a variant of K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
on the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of Banach algebras (In most applications, these Banach algebras are C*-algebras).
Its basic feature that distinguishes it from algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
is that it has a Bott periodicity. So there are only two K-groups, namely
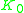, equal to algebraic 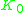, and 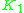. As a consequence of the periodicity theorem, it satisfies excisionExcision
Excision is the alias of Jeff Abel, a dubstep DJ and music boss from British Columbia, Canada. He frequently works with fellow Canadian dubstep producers Datsik and Downlink. As one of the first dubstep producers and DJs in North America, he has played a significant role in the genre's growth in...
. This means that it associates to an extension of C*-algebras to a long exact sequence, which, by Bott periodicity, reduces to an exact cyclic 6-term-sequence.
Operator K-theory is a generalization of topological K-theory
Topological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
, defined by means of vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s on locally compact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s. Here, an n-dimensional vector bundle over a topological space X is associated to a projection in
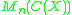, where 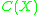is the C* algebra of continuous functions over X. Also, it is known that homotopy equivalence of vector bundles translates to Murray-von Neumann equivalence of the associated projection in K⊗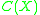, where K is compact operators on a separable Hilbert space.Hence, the
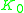group of a (not necessarily commutative) C* algebra A is defined as Grothendieck groupGrothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
generated by the Murray-von Neumann equivalence classes of projections in K⊗
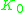. is a functor from the category of C* Algebras and *-homomorphisms, to the category of abelian groups and group homomorphisms. The higher K-functors are defined via a C*-version of the suspension: 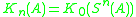whereHowever, by Bott periodicity, it turns out that
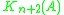and 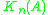are isomorphic for each n, and thus the only groups produced by this construction are 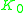and 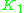.The key reason for the introduction of K-theoretic methods into the study of C*-algebras was the Fredholm index: Given a bounded linear operator on a Hilbert space that has finite dimensional kernel and co-kernel, one can associate to it an integer, which, as it turns out, reflects the 'defect' on the operator - i.e. the extent to which it is not invertible. In analysis on manifolds, this index and its generalizations played a crucial role in the index theory of Atiyah and Singer, where the topological index of the manifold can be expressed via the index of elliptic operators on it. Later on, Brown, Douglas and Fillmore observed that the Fredholm index was the missing ingredient in classifying essentially normal operators up to certain natural equivalence. These ideas, together with Elliott's classification of AF C*-algebras via K-theory led to a great deal of interest in adapting methods such as K-theory from algebraic topology into the study of operator algebras.
This, in turn, led to K-homology
K-homology
In mathematics, K-homology is a homology theory on the category of compact Hausdorff spaces. It classifies the elliptic pseudo-differential operators acting on the vector bundles over a space...
, Kasparov's bivariant KK-Theory
KK-theory
In mathematics, KK-theory is a common generalization both of K-homology and K-theory , as an additive bivariant functor on separable C*-algebras...
, and, more recently, Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and Higson's E-theory.