
Banach limit
Encyclopedia
In mathematical analysis
, a Banach limit is a continuous
linear functional
 defined on the Banach space
defined on the Banach space
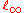 of all bounded complex
of all bounded complex
-valued sequence
s such that for any sequences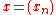 and
and 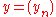 , the following conditions are satisfied:
, the following conditions are satisfied:
 is an extension of the continuous functional
is an extension of the continuous functional

In other words, a Banach limit extends the usual limits, is shift-invariant and positive. However, there exist sequences for which the values of two Banach limits do not agree. We say that the Banach limit is not uniquely determined in this case. However, as a consequence of the above properties, a Banach limit also satisfies:
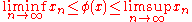
The existence of Banach limits is usually proved using the Hahn–Banach theorem
(analyst's approach) or using ultrafilter
s (this approach is more frequent in set-theoretical expositions). It is worth mentioning, that these proofs use the Axiom of choice (so called non-effective proof).
For example, if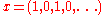 ,
,
then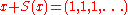 is a constant sequence, and
is a constant sequence, and 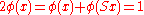 holds. Thus for any Banach limit this sequence has limit
holds. Thus for any Banach limit this sequence has limit  .
.
A sequence with the property, that for every Banach limit
with the property, that for every Banach limit  the value
the value 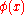 is the same, is called almost convergent.
is the same, is called almost convergent.
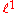 . Thus the Banach limit on
. Thus the Banach limit on 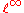 is an example of an element of the continuous dual space
is an example of an element of the continuous dual space 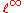 which is not in
which is not in 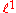 . The dual of
. The dual of 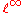 is known as the ba space
is known as the ba space
, and consists of all finitely additive measures on the sigma-algebra of all subsets of the natural numbers.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a Banach limit is a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
 defined on the Banach space
defined on the Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
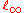 of all bounded complex
of all bounded complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s such that for any sequences
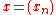 and
and 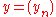 , the following conditions are satisfied:
, the following conditions are satisfied:
-
 (linearity);
(linearity); - if
 for all
for all  , then
, then 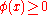 ;
; -
 , where
, where 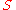 is the shift operatorShift operatorIn mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
is the shift operatorShift operatorIn mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
defined by .
. - If
 is a convergent sequence, then
is a convergent sequence, then  . Hence,
. Hence,
 is an extension of the continuous functional
is an extension of the continuous functional
In other words, a Banach limit extends the usual limits, is shift-invariant and positive. However, there exist sequences for which the values of two Banach limits do not agree. We say that the Banach limit is not uniquely determined in this case. However, as a consequence of the above properties, a Banach limit also satisfies:
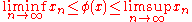
The existence of Banach limits is usually proved using the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
(analyst's approach) or using ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s (this approach is more frequent in set-theoretical expositions). It is worth mentioning, that these proofs use the Axiom of choice (so called non-effective proof).
Almost convergence
There are non-convergent sequences which have uniquely determined Banach limits.For example, if
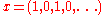 ,
,then
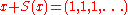 is a constant sequence, and
is a constant sequence, and 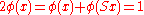 holds. Thus for any Banach limit this sequence has limit
holds. Thus for any Banach limit this sequence has limit  .
.A sequence
 with the property, that for every Banach limit
with the property, that for every Banach limit  the value
the value 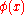 is the same, is called almost convergent.
is the same, is called almost convergent.Ba spaces
Given a sequence in c, the ordinary limit of the sequence does not arise from an element of . Thus the Banach limit on
. Thus the Banach limit on 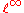 is an example of an element of the continuous dual space
is an example of an element of the continuous dual space 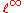 which is not in
which is not in 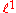 . The dual of
. The dual of 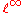 is known as the ba space
is known as the ba spaceBa space
In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|....
, and consists of all finitely additive measures on the sigma-algebra of all subsets of the natural numbers.

