Almost convergent sequence
Encyclopedia
A bounded real
sequence
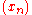is said to be almost convergent to 
if each Banach limit assigns
the same value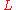
to the sequence 
.
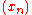Lorentz proved that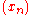
is almost convergent if and only if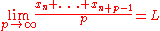
uniformly in
.
The above limit can be rewritten in detail as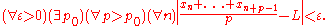
Almost convergence is studied in summability theory. It is an example of a summability method
which cannot be represented as a matrix method.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
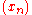is said to be almost convergent to if each Banach limit assignsthe same value
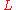to the sequence 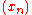.Lorentz proved that
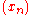is almost convergent if and only if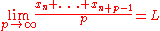uniformly in
.The above limit can be rewritten in detail as
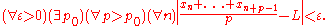
Almost convergence is studied in summability theory. It is an example of a summability method
which cannot be represented as a matrix method.