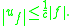Babuška-Lax-Milgram theorem
Encyclopedia
In mathematics
, the Babuška–Lax–Milgram theorem is a generalization of the famous Lax–Milgram theorem, which gives conditions under which a bilinear form can be "inverted" to show the existence and uniqueness of a weak solution
to a given boundary value problem
. The result is named after the mathematician
s Ivo Babuška
, Peter Lax
and Arthur Milgram
.
approach to the study of partial differential equations, one does not attempt to solve a given partial differential equation directly, but by using the structure of the vector space
of possible solutions, e.g. a Sobolev space
Wk,p. Abstractly, consider two real
normed spaces U and V with their continuous dual spaces U∗ and V∗ respectively. In many applications, U is the space of possible solutions; given some partial differential operator Λ : U → V∗ and a specified element f ∈ V∗, the objective is to find a u ∈ U such that
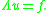
However, in the weak formulation
, this equation is only required to hold when "tested" against all other possible elements of V. This "testing" is accomplished by means of a bilinear function B : U × V → R which encodes the differential operator Λ; a weak solution to the problem is to find a u ∈ U such that
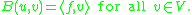
The achievement of Lax and Milgram in their 1954 result was to specify sufficient conditions for this weak formulation to have a unique solution that depends continuously
upon the specified datum f ∈ V∗: it suffices that U = V is a Hilbert space
, that B is continuous, and that B is strongly coercive
, i.e.
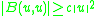
for some constant c > 0 and all u ∈ U.
For example, in the solution of the Poisson equation on a bounded
, open
domain Ω ⊂ Rn,
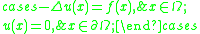
the space U could be taken to be the Sobolev space H01(Ω) with dual H−1(Ω); the former is a subspace of the Lp space
V = L2(Ω); the bilinear form B associated to −Δ is the L2(Ω) inner product of the derivatives:
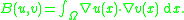
Hence, the weak formulation of the Poisson equation, given f ∈ L2(Ω), is to find uf such that
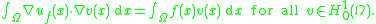
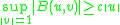
and, for 0 ≠ v ∈ V,
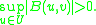
Then, for all f ∈ V∗, there exists a unique solution u = uf ∈ U to the weak problem
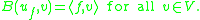
Moreover, the solution depends continuously on the given datum:
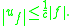
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Babuška–Lax–Milgram theorem is a generalization of the famous Lax–Milgram theorem, which gives conditions under which a bilinear form can be "inverted" to show the existence and uniqueness of a weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
to a given boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
. The result is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Ivo Babuška
Ivo Babuška
Ivo M. Babuška is a Czech-American mathematician, noted for his studies of the finite element method and the proof of the Babuška-Lax-Milgram theorem in partial differential equations. One of the celebrated result in the finite elements is the so-called Babuska-Brezzi condition, which provides...
, Peter Lax
Peter Lax
Peter David Lax is a mathematician working in the areas of pure and applied mathematics. He has made important contributions to integrable systems, fluid dynamics and shock waves, solitonic physics, hyperbolic conservation laws, and mathematical and scientific computing, among other fields...
and Arthur Milgram
Arthur Milgram
Arthur Norton Milgram was an American mathematician. He made contributions in functional analysis, combinatorics, differential geometry, topology, partial differential equations, and Galois theory...
.
Background
In the modern, functional-analyticFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
approach to the study of partial differential equations, one does not attempt to solve a given partial differential equation directly, but by using the structure of the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of possible solutions, e.g. a Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
Wk,p. Abstractly, consider two real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
normed spaces U and V with their continuous dual spaces U∗ and V∗ respectively. In many applications, U is the space of possible solutions; given some partial differential operator Λ : U → V∗ and a specified element f ∈ V∗, the objective is to find a u ∈ U such that
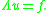
However, in the weak formulation
Weak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
, this equation is only required to hold when "tested" against all other possible elements of V. This "testing" is accomplished by means of a bilinear function B : U × V → R which encodes the differential operator Λ; a weak solution to the problem is to find a u ∈ U such that
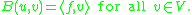
The achievement of Lax and Milgram in their 1954 result was to specify sufficient conditions for this weak formulation to have a unique solution that depends continuously
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
upon the specified datum f ∈ V∗: it suffices that U = V is a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, that B is continuous, and that B is strongly coercive
Coercive function
In mathematics, a coercive function is a function that "grows rapidly" at the extremes of the space on which it is defined. More precisely, a function f : Rn → Rn is called coercive if...
, i.e.
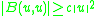
for some constant c > 0 and all u ∈ U.
For example, in the solution of the Poisson equation on a bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
domain Ω ⊂ Rn,
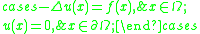
the space U could be taken to be the Sobolev space H01(Ω) with dual H−1(Ω); the former is a subspace of the Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
V = L2(Ω); the bilinear form B associated to −Δ is the L2(Ω) inner product of the derivatives:
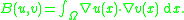
Hence, the weak formulation of the Poisson equation, given f ∈ L2(Ω), is to find uf such that
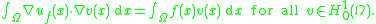
Statement of the theorem
In 1971, Babuška provided the following generalization of Lax and Milgram's earlier result, which begins by dispensing with the requirement that U and V be the same space. Let U and V be two real Hilbert spaces and let B : U × V → R be a continuous bilinear function. Suppose also that B is weakly coercive: for some constant c > 0 and all u ∈ U,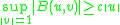
and, for 0 ≠ v ∈ V,
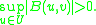
Then, for all f ∈ V∗, there exists a unique solution u = uf ∈ U to the weak problem
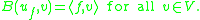
Moreover, the solution depends continuously on the given datum: