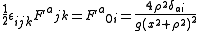BPST instanton
Encyclopedia
The BPST instanton is the instanton
with winding number
1 found by Alexander Belavin
, Alexander Polyakov, Albert Schwarz
and Yu. S. Tyupkin. It is a classical solution to the equations of motion of SU(2) Yang-Mills theory in Euclidean space-time (i.e. after Wick rotation
), meaning it describes a transition between two different vacua
of the theory. It was originally hoped to open the path to solving the problem of confinement, especially since Polyakov had proven in 1987 that instantons are the cause of confinement in three-dimensional compact-QED. This hope was not realized, however.
The BPST instanton is an essentially non-perturbative classical solution of the Yang-Mills field equations. It is found when minimizing the Yang-Mills SU(2) Lagrangian
:
with Fμνa = ∂μAνa – ∂νAμa + gεabcAμbAνc the field strength
. The instanton is a solution with finite action, so that Fμν must go to zero at space-time infinity, meaning that Aμ goes to a pure gauge configuration. Space-time infinity of our four-dimensional world is S3. The gauge group SU(2) has exactly the same structure, so the solutions with Aμ pure gauge at infinity are mappings from S3 onto itself. These mappings can be labelled by an integer number q, the Pontryagin index (or winding number
). Instantons have q = 1 and thus correspond (at infinity) to gauge transformations which cannot be continuously deformed to unity. The BPST solution is thus topologically stable.
It can be shown that self-dual configurations obeying the relation Fμνa = ± ½ εμναβ Fαβa minimize the action. Solutions with a plus sign are called instantons, those with the minus sign are anti-instantons.
Instantons and anti-instantons can be shown to minimise the action locally as follows:
The first term is minimised by self-dual or anti-self-dual configurations, whereas the last term is a total derivative and therefore depends only on the boundary (i.e.
) of the solution; it is therefore a topological invariant and can be shown to be an integer number times some constant (the constant here is 
). The integer is called instanton number (see Homotopy group
).
Explicitly the instanton solution is given by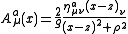
with zμ the center and ρ the scale of the instanton. ηaμν is the 't Hooft symbol
:
For large x2, ρ becomes negligible and the gauge field approaches that of the pure gauge transformation:
. Indeed, the field strength is:
and approaches zero as fast as r-4 at infinity.
An anti-instanton is described by a similar expression, but with the 't Hooft symbol replaced by the anti-'t Hooft symbol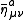
, which is equal to the ordinary 't Hooft symbol, except that the components with one of the Lorentz indices equal to four have opposite sign.
The BPST solution has many symmetries. Translation
s and dilation
s transform a solution into other solutions. Coordinate inversion (xμ → xμ/x2) transforms an instanton of size ρ into an anti-instanton with size 1/ρ and vice versa. Rotation
s in Euclidean four-space and special conformal transformations leave the solution invariant (up to a gauge transformation).
The classical action of an instanton equals
Since this quantity comes in an exponential in the path integral formalism
this is an essentially non-perturbative effect, as the function e–1/x has no Taylor series
.
In singular gauge, the expression has a singularity in the center of the instanton, but goes to zero more swiftly for x to infinity.
When working in other gauges than the Landau gauge, similar expressions can be found in the literature.
.
The above is valid for a Yang-Mills theory with SU(2) as gauge group. It can readily be generalized to an arbitrary non-Abelian group. The instantons are then given by the BPST instanton for some directions in the group space, and by zero in the other directions.
When turning to a Yang-Mills theory with spontaneous symmetry breaking
due to the Higgs mechanism
, one finds that BPST instantons are not exact solutions to the field equations anymore. In order to find approximate solutions, the formalism of constrained instantons can be used.
. Instantons are indeed found in lattice
calculations. The first computations performed with instantons used the dilute gas approximation. The results obtained did not solve the infrared problem of QCD, making many physicists turn away from instanton physics. Later, though, an instanton liquid model
was proposed, turning out to be more promising an approach.
The dilute instanton gas model departs from the supposition that the QCD vacuum consists of a gas of BPST instantons. Although only the solutions with one or few instantons (or anti-instantons) are known exactly, a dilute gas of instantons and anti-instantons can be approximated by considering a superposition of one-instanton solutions at great distances from one another. 't Hooft calculated the effective action for such an ensemble, and he found an infrared divergence
for big instantons, meaning that an infinite amount of infinitely big instantons would populate the vacuum.
Later, an instanton liquid model
was studied. This model starts from the assumption that an ensemble of instantons cannot be described by a mere sum of separate instantons. Various models have been proposed, introducing interactions between instantons or using variational methods (like the "valley approximation") endeavouring to approximate the exact multi-instanton solution as closely as possible. Many phenomenological successes have been reached. Confinement seems to be the biggest issue in Yang-Mills theory for which instantons have no answer whatsoever.
interaction is described by SU(2), so that instantons can be expected to play a role there as well. If so, they would induce baryon number violation. Due to the Higgs mechanism
, instantons are not exact solutions anymore, but approximations can be used instead. One of the conclusions is that the presence of a gauge boson mass suppresses large instantons, so that the instanton gas approximation is consistent.
Due to the non-perturbative nature of instantons, all their effects are suppressed by a factor of e–16π²/g², which, in electroweak theory, is of the order 10–179.
Solutions which are not self-dual also exist. These are not local minima of the action, but instead they correspond to saddle points.
Instantons are also closely related to meron
s, singular non-dual solutions of the Euclidian Yang-Mills field equations of topological charge 1/2. Instantons are thought to be composed of two merons.
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
with winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
1 found by Alexander Belavin
Alexander Belavin
Alexander "Sasha" Abramovich Belavin is a Russian physicist, known for his contributions to string theory.He is a professor at the Independent University of Moscow and is researcher at the Landau Institute of Theoretical Physics....
, Alexander Polyakov, Albert Schwarz
Albert Schwarz
Albert S. Schwarz is a mathematician and a theoretical physicist educated in Soviet Union and now a Professor at the University of California-Davis. He is one of the pioneers of Morse theory and brought up the first example of a topological quantum field theory. Schwarz worked on some examples in...
and Yu. S. Tyupkin. It is a classical solution to the equations of motion of SU(2) Yang-Mills theory in Euclidean space-time (i.e. after Wick rotation
Wick rotation
In physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable...
), meaning it describes a transition between two different vacua
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
of the theory. It was originally hoped to open the path to solving the problem of confinement, especially since Polyakov had proven in 1987 that instantons are the cause of confinement in three-dimensional compact-QED. This hope was not realized, however.
The instanton
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
:
with Fμνa = ∂μAνa – ∂νAμa + gεabcAμbAνc the field strength
Field strength
In physics, the field strength of a field is the magnitude of its vector value.In theoretical physics, field strength is another name for the curvature form...
. The instanton is a solution with finite action, so that Fμν must go to zero at space-time infinity, meaning that Aμ goes to a pure gauge configuration. Space-time infinity of our four-dimensional world is S3. The gauge group SU(2) has exactly the same structure, so the solutions with Aμ pure gauge at infinity are mappings from S3 onto itself. These mappings can be labelled by an integer number q, the Pontryagin index (or winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
). Instantons have q = 1 and thus correspond (at infinity) to gauge transformations which cannot be continuously deformed to unity. The BPST solution is thus topologically stable.
It can be shown that self-dual configurations obeying the relation Fμνa = ± ½ εμναβ Fαβa minimize the action. Solutions with a plus sign are called instantons, those with the minus sign are anti-instantons.
Instantons and anti-instantons can be shown to minimise the action locally as follows:
-
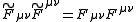, where 
.
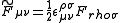The first term is minimised by self-dual or anti-self-dual configurations, whereas the last term is a total derivative and therefore depends only on the boundary (i.e.
) of the solution; it is therefore a topological invariant and can be shown to be an integer number times some constant (the constant here is ). The integer is called instanton number (see Homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
).
Explicitly the instanton solution is given by
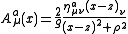
with zμ the center and ρ the scale of the instanton. ηaμν is the 't Hooft symbol
't Hooft symbol
The t Hooft η symbol is a symbol which allows one to express the generators of the SU Lie algebra in terms of the generators of Lorentz algebra. The symbol is a blend between the Kronecker delta and the Levi-Civita symbol. It was introduced by Gerard 't Hooft...
:
For large x2, ρ becomes negligible and the gauge field approaches that of the pure gauge transformation:
. Indeed, the field strength is:
and approaches zero as fast as r-4 at infinity.
An anti-instanton is described by a similar expression, but with the 't Hooft symbol replaced by the anti-'t Hooft symbol
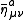, which is equal to the ordinary 't Hooft symbol, except that the components with one of the Lorentz indices equal to four have opposite sign.The BPST solution has many symmetries. Translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s and dilation
Dilation (mathematics)
In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
s transform a solution into other solutions. Coordinate inversion (xμ → xμ/x2) transforms an instanton of size ρ into an anti-instanton with size 1/ρ and vice versa. Rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s in Euclidean four-space and special conformal transformations leave the solution invariant (up to a gauge transformation).
The classical action of an instanton equals
Since this quantity comes in an exponential in the path integral formalism
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
this is an essentially non-perturbative effect, as the function e–1/x has no Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
.
Other gauges
The expression for the BPST instanton given above is in the so-called regular Landau gauge. Another form exists, which is gauge-equivalent with the expression given above, in the singular Landau gauge. In both these gauges, the expression satisfies ∂μAμ = 0. In singular gauge the instanton isIn singular gauge, the expression has a singularity in the center of the instanton, but goes to zero more swiftly for x to infinity.
When working in other gauges than the Landau gauge, similar expressions can be found in the literature.
Generalization and embedding in other theories
At finite temperature the BPST instanton generalizes to what is called a caloronCaloron
In mathematical physics, a caloron is the finite temperature generalization of an instanton.-Finite temperature and instantons:At zero temperature, instantons are the name given to solutions of the classical equations of motion of the Euclidean version of the theory under consideration, and which...
.
The above is valid for a Yang-Mills theory with SU(2) as gauge group. It can readily be generalized to an arbitrary non-Abelian group. The instantons are then given by the BPST instanton for some directions in the group space, and by zero in the other directions.
When turning to a Yang-Mills theory with spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
due to the Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
, one finds that BPST instantons are not exact solutions to the field equations anymore. In order to find approximate solutions, the formalism of constrained instantons can be used.
In QCD
It is expected that BPST-like instantons play an important role in the vacuum structure of QCDQCD vacuum
The QCD vacuum is the vacuum state of quantum chromodynamics . It is an example of a non-perturbative vacuum state, characterized by many non-vanishing condensates such as the gluon condensate or the quark condensate...
. Instantons are indeed found in lattice
Lattice QCD
Lattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time....
calculations. The first computations performed with instantons used the dilute gas approximation. The results obtained did not solve the infrared problem of QCD, making many physicists turn away from instanton physics. Later, though, an instanton liquid model
Instanton fluid
In quantum chromodynamics, the instanton fluid model is a model of Wick rotated Euclidean quantum chromodynamics. If we examine the path integral of the action, we find that it has infinitely many local minima, corresponding to varying instanton numbers...
was proposed, turning out to be more promising an approach.
The dilute instanton gas model departs from the supposition that the QCD vacuum consists of a gas of BPST instantons. Although only the solutions with one or few instantons (or anti-instantons) are known exactly, a dilute gas of instantons and anti-instantons can be approximated by considering a superposition of one-instanton solutions at great distances from one another. 't Hooft calculated the effective action for such an ensemble, and he found an infrared divergence
Infrared divergence
In physics, an infrared divergence or infrared catastrophe is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very small energy approaching zero, or, equivalently, because of physical phenomena at very long distances.The infrared ...
for big instantons, meaning that an infinite amount of infinitely big instantons would populate the vacuum.
Later, an instanton liquid model
Instanton fluid
In quantum chromodynamics, the instanton fluid model is a model of Wick rotated Euclidean quantum chromodynamics. If we examine the path integral of the action, we find that it has infinitely many local minima, corresponding to varying instanton numbers...
was studied. This model starts from the assumption that an ensemble of instantons cannot be described by a mere sum of separate instantons. Various models have been proposed, introducing interactions between instantons or using variational methods (like the "valley approximation") endeavouring to approximate the exact multi-instanton solution as closely as possible. Many phenomenological successes have been reached. Confinement seems to be the biggest issue in Yang-Mills theory for which instantons have no answer whatsoever.
In electroweak theory
The weak interactionWeak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
interaction is described by SU(2), so that instantons can be expected to play a role there as well. If so, they would induce baryon number violation. Due to the Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
, instantons are not exact solutions anymore, but approximations can be used instead. One of the conclusions is that the presence of a gauge boson mass suppresses large instantons, so that the instanton gas approximation is consistent.
Due to the non-perturbative nature of instantons, all their effects are suppressed by a factor of e–16π²/g², which, in electroweak theory, is of the order 10–179.
Other solutions to the field equations
The instanton and anti-instantons are not the only solutions of the Wick-rotated Yang-Mills field equations. Multi-instanton solutions have been found for q equal to two and three, and partial solutions exist for higher q as well. General multi-instanton solutions can only be approximated using the valley approximation — one starts from a certain ansatz (usually the sum of the required number of instantons) and one minimizes numerically the action under a given constraint (keeping the number of instantons and the sizes of the instantons constant).Solutions which are not self-dual also exist. These are not local minima of the action, but instead they correspond to saddle points.
Instantons are also closely related to meron
Meron
A meron or half-instanton is a Euclidean space-time solution of the Yang-Mills field equations. It is a singular non-self-dual solution of topological charge 1/2. The instanton is believed to be composed of two merons....
s, singular non-dual solutions of the Euclidian Yang-Mills field equations of topological charge 1/2. Instantons are thought to be composed of two merons.