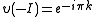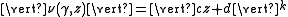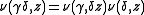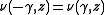Automorphic factor
Encyclopedia
In mathematics
, an automorphic factor is a certain type of analytic function
, defined on subgroup
s of SL(2,R), appearing in the theory of modular form
s. The general case, for general groups, is reviewed in the article 'factor of automorphy
'.
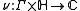
satisfying the four properties given below. Here, the notation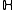 and
and 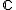 refer to the upper half-plane and the complex plane
refer to the upper half-plane and the complex plane
, respectively. The notation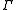 is a subgroup of SL(2,R), such as, for example, a Fuchsian group
is a subgroup of SL(2,R), such as, for example, a Fuchsian group
. An element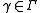 is a 2x2 matrix
is a 2x2 matrix
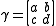
with a, b, c, d real numbers, satisfying ad−bc=1.
An automorphic factor must satisfy:
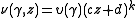
with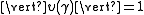
The function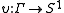 is called a multiplier system. Clearly,
is called a multiplier system. Clearly,
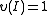 ,
,
while, if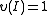 , then
, then
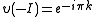
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an automorphic factor is a certain type of analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, defined on subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of SL(2,R), appearing in the theory of modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s. The general case, for general groups, is reviewed in the article 'factor of automorphy
Factor of automorphy
In mathematics, the notion of factor of automorphy arises for a group acting on a complex-analytic manifold. Suppose a group G acts on a complex-analytic manifold X. Then, G also acts on the space of holomorphic functions from X to the complex numbers. A function f is termed an automorphic form if...
'.
Definition
An automorphic factor of weight k is a function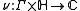
satisfying the four properties given below. Here, the notation
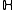 and
and 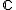 refer to the upper half-plane and the complex plane
refer to the upper half-plane and the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, respectively. The notation
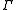 is a subgroup of SL(2,R), such as, for example, a Fuchsian group
is a subgroup of SL(2,R), such as, for example, a Fuchsian groupFuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
. An element
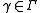 is a 2x2 matrix
is a 2x2 matrix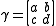
with a, b, c, d real numbers, satisfying ad−bc=1.
An automorphic factor must satisfy:
- 1. For a fixed
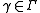 , the function
, the function 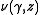 is a holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
is a holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
of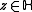 .
.
- 2. For all
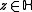 and
and 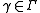 , one has
, one has
- for a fixed real number k.
- 3. For all
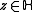 and
and 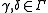 , one has
, one has
- Here,
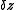 is the fractional linear transform of
is the fractional linear transform of  by
by 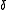 .
.
- 4.If
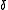 , then for all
, then for all 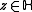 and
and 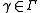 , one has
, one has
- Here, I denotes the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
Properties
Every automorphic factor may be written as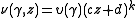
with
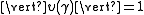
The function
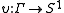 is called a multiplier system. Clearly,
is called a multiplier system. Clearly,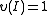 ,
,while, if
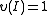 , then
, then