
Arthur–Selberg trace formula
Encyclopedia
In mathematics, the Arthur–Selberg trace formula is a generalization of the Selberg trace formula
from the group SL2 to arbitrary reductive group
s over global fields, developed by James Arthur
in a long series of papers from 1974 to 2003.
It describes the character of the representation of G(A) on the discrete part L(G(F)∖G(A)) of L2(G(F)∖G(A)) in terms of geometric data, where G is a reductive algebraic group defined over a global field F and A is the ring of adeles
of F.
There are several different versions of the trace formula. The first version was the unrefined trace formula, whose terms depend on truncation operators and have the disadvantage that they are not invariant. Arthur later found the invariant trace formula and the stable trace formula which are more suitable for applications. The simple trace formula is less general but easier to prove. The local trace formula
is an analogue over local fields.
Jacquet's relative trace formula is a generalization where one integrates the kernel function over non-diagonal subgroups.
.
In the compact case, which is essentially due to Selberg, the groups G(F) and G(A) can be replaced by any
discrete subgroup Γof a locally compact group G with Γ\G compact. The group G acts on the space of functions on
Γ∖G by the right regular representation R, and this extends to an action of the group ring of G, considered as the ring of functions f on G. The character of this representation is given by a generalization of the Frobenius formula as follows.
The action of a function f on a function φ on Γ∖G is given by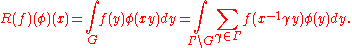
In other words R(f) is an integral operator on L2(Γ∖G) (the space of functions on Γ∖G) with kernel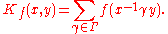
Therefore the trace of R(f) is given by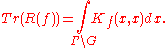
The kernel K can be written as
where O is the set of conjugacy classes in Γ, and
where γ is an element of the conjugacy class o, and Γγ is its centralizer in Γ.
On the other hand, the trace is also given by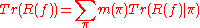
where m(π) is the multiplicity of the irreducible unitary representation π of G in L2(Γ∖G).
Arthur dealt with these problems by truncating the kernel at cusps in such a way that the truncated kernel is integrable over the diagonal. This truncation process causes many problems; for example, the truncated terms are no longer invariant under conjugation. By manipulating the terms further, Arthur was able to produce an invariant trace formula whose terms are invariant.
The original Selberg trace formula studied a discrete subgroup Γ of a real Lie group G(R) (usually SL2(R)).
In higher rank it is more convenient to replace the Lie group with an adelic group G(A). One reason for this that the discrete group can be taken as the group of points G(F) for F a (global) field, which is easier to work with
than discrete subgroups of Lie groups. It also makes Hecke operator
s easier to work with.

The left hand side is the geometric side of the trace formula, and is a sum over equivalence classes in the group of rational points G(F) of G, while the right hand side is the spectral side of the trace formula and is a sum over certain representations of subgroups of G(A).
The invariant trace formula states
where
Two elements of a group G(F) are called stably conjugate if they are conjugate over
the algebraic closure of the field F. The point is that when one compares elements in two different groups, related for example by inner twisting, one does not usually get a good correspondence between conjugacy classes, but only between stable conjugacy classes. So to compare the geometric terms in the trace formulas for two different groups, one would like the terms to be not just invariant under conjugacy, but also to be well behaved on stable conjugacy classes; these are called stable distributions.
The stable trace formula writes the terms in the trace formula of a group G in terms of stable distributions. However these stable distributions are not distributions on the group G, but are distributions on a family of quasisplit groups called the endoscopic group
s of G. Unstable orbital integrals on the group G correspond to stable orbital integrals on its endoscopic groups H.
For example, if the functions f are cuspidal, which means that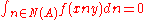
for any unipotent radical N of a proper parabolic subgroup (defined over F) and any x, y in G(A), then the operator R(f) has image in the space of cusp forms so is compact.
some groups.
used the Arthur–Selberg trace formula to prove the Weil conjecture on Tamagawa numbers
.
described how the trace formula is used in his proof of the Langlands conjecture for general linear groups over function fields.
Selberg trace formula
In mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
from the group SL2 to arbitrary reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
s over global fields, developed by James Arthur
James Arthur (mathematician)
James Greig Arthur , is a Canadian mathematician and former President of the American Mathematical Society. He is currently in the Mathematics Departmentof the University of Toronto....
in a long series of papers from 1974 to 2003.
It describes the character of the representation of G(A) on the discrete part L(G(F)∖G(A)) of L2(G(F)∖G(A)) in terms of geometric data, where G is a reductive algebraic group defined over a global field F and A is the ring of adeles
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
of F.
There are several different versions of the trace formula. The first version was the unrefined trace formula, whose terms depend on truncation operators and have the disadvantage that they are not invariant. Arthur later found the invariant trace formula and the stable trace formula which are more suitable for applications. The simple trace formula is less general but easier to prove. The local trace formula
Local trace formula
In mathematics, the local trace formula is a local analogue of the Arthur–Selberg trace formula that describes the character of the representation of G on the discrete part of L2, for G a reductive algebraic group over a local field F.-References: | year=1991 | journal=Publications Mathématiques...
is an analogue over local fields.
Jacquet's relative trace formula is a generalization where one integrates the kernel function over non-diagonal subgroups.
Notation
- A is the ring of adeles of F.
- F is a global fieldGlobal fieldIn mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
, such as the field of rational numbers. - G is a reductive algebraic group defined over F.
The compact case
In the (rare) case when G(F)∖G(A) is compact the representation splits as a direct sum of irreducible representations, and the trace formula is similar to the Frobenius formula for the character of the representation induced from the trivial representation of a subgroup of finite indexIndex of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
.
In the compact case, which is essentially due to Selberg, the groups G(F) and G(A) can be replaced by any
discrete subgroup Γof a locally compact group G with Γ\G compact. The group G acts on the space of functions on
Γ∖G by the right regular representation R, and this extends to an action of the group ring of G, considered as the ring of functions f on G. The character of this representation is given by a generalization of the Frobenius formula as follows.
The action of a function f on a function φ on Γ∖G is given by
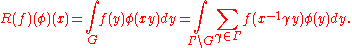
In other words R(f) is an integral operator on L2(Γ∖G) (the space of functions on Γ∖G) with kernel
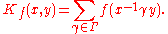
Therefore the trace of R(f) is given by
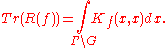
The kernel K can be written as

where O is the set of conjugacy classes in Γ, and

where γ is an element of the conjugacy class o, and Γγ is its centralizer in Γ.
On the other hand, the trace is also given by
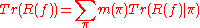
where m(π) is the multiplicity of the irreducible unitary representation π of G in L2(Γ∖G).
Examples
- If Γ and G are both finite, the trace formula is equivalent to the Frobenius formula for the character of an induced representation.
- If G is the group R of real numbers and Γ the subgroup Z of integers, then the trace formula becomes the Poisson summation formulaPoisson summation formulaIn mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...
.
Difficulties in the non-compact case
In most cases of the Arthur–Selberg trace formula, the quotient G(F)∖G(A) is not compact, which causes the following (closely related) problems:- The representation on L2(G(F)∖G(A)) contains not only discrete components, but also continuous components.
- The kernel is no longer integrable over the diagonal, and the operators R(f) are no longer of trace class.
Arthur dealt with these problems by truncating the kernel at cusps in such a way that the truncated kernel is integrable over the diagonal. This truncation process causes many problems; for example, the truncated terms are no longer invariant under conjugation. By manipulating the terms further, Arthur was able to produce an invariant trace formula whose terms are invariant.
The original Selberg trace formula studied a discrete subgroup Γ of a real Lie group G(R) (usually SL2(R)).
In higher rank it is more convenient to replace the Lie group with an adelic group G(A). One reason for this that the discrete group can be taken as the group of points G(F) for F a (global) field, which is easier to work with
than discrete subgroups of Lie groups. It also makes Hecke operator
Hecke operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations....
s easier to work with.
The trace formula in the non-compact case
One version of the trace formula asserts the equality of two distributions on G(A):
The left hand side is the geometric side of the trace formula, and is a sum over equivalence classes in the group of rational points G(F) of G, while the right hand side is the spectral side of the trace formula and is a sum over certain representations of subgroups of G(A).
The invariant trace formula
The version of the trace formula above is not particularly easy to use in practice, one of the problems being that the terms in it are not invariant under conjugation. found a modification in which the terms are invariant.The invariant trace formula states

where
- f is a test function on G(A)
- M ranges over a finite set of rational Levi subgroups of G
- (M(Q)) is the set of conjugacy classes of M(Q)
- Π(M) is the set of irreducible unitary representations of M(A)
- aM(γ) is related to the volume of M(Q,γ)\M(A,γ)
- aM(π) is related to the multiplicity of the irreducible representation π in L2(M(Q)\M(A))
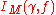 is related to
is related to 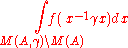
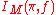 is related to trace
is related to trace 
- W0(M) is the Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of M.
Stable trace formula
suggested the possibility a stable refinement of the trace formula that can be used to compare the trace formula for two different groups. Such a stable trace formula was found and proved by .Two elements of a group G(F) are called stably conjugate if they are conjugate over
the algebraic closure of the field F. The point is that when one compares elements in two different groups, related for example by inner twisting, one does not usually get a good correspondence between conjugacy classes, but only between stable conjugacy classes. So to compare the geometric terms in the trace formulas for two different groups, one would like the terms to be not just invariant under conjugacy, but also to be well behaved on stable conjugacy classes; these are called stable distributions.
The stable trace formula writes the terms in the trace formula of a group G in terms of stable distributions. However these stable distributions are not distributions on the group G, but are distributions on a family of quasisplit groups called the endoscopic group
Endoscopic group
In mathematics, endoscopic groups of reductive algebraic groups were introduced by in his work on the stable trace formula.Roughly speaking, an endoscopic group H of G is a quasi-split group whose L-group is the connected component of the centralizer of a semisimple element of the L-group of G.In...
s of G. Unstable orbital integrals on the group G correspond to stable orbital integrals on its endoscopic groups H.
Simple trace formula
There are several simple forms of the trace formula, which restrict the compactly supported test functions f in some way . The advantage of this is that the trace formula and its proof become much easier, and the disadvantage is that the resulting formula is less powerful.For example, if the functions f are cuspidal, which means that
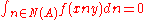
for any unipotent radical N of a proper parabolic subgroup (defined over F) and any x, y in G(A), then the operator R(f) has image in the space of cusp forms so is compact.
Applications
used the Selberg trace formula to prove the Jacquet-Langlands correspondence between automorphic forms on GL2 and its twisted forms. The Arthur–Selberg trace formula can be used to study similar correspondences on higher rank groups. It can also be used to prove several other special cases of Langlands functoriality, such as base change, forsome groups.
used the Arthur–Selberg trace formula to prove the Weil conjecture on Tamagawa numbers
Weil conjecture on Tamagawa numbers
In mathematics, the Weil conjecture on Tamagawa numbers is a result about algebraic groups formulated by André Weil in the late 1950s and proved in 1989...
.
described how the trace formula is used in his proof of the Langlands conjecture for general linear groups over function fields.

