
Difference set
Encyclopedia
In combinatorics
, a difference set is a subset
difference set is a subset
 of a group
of a group
 such that the order of
such that the order of  is
is  , the size of
, the size of  is
is 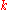 , and every nonidentity element of
, and every nonidentity element of  can be expressed as a product
can be expressed as a product 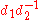 of elements of
of elements of  in exactly
in exactly 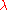 ways.
ways.
 and not dividing v, then the group automorphism defined by
and not dividing v, then the group automorphism defined by  fixes some translate of D. It is known to be true for
fixes some translate of D. It is known to be true for  , and this is known as the First Multiplier Theorem. A more general known result, the Second Multiplier Theorem, first says to choose a divisor
, and this is known as the First Multiplier Theorem. A more general known result, the Second Multiplier Theorem, first says to choose a divisor  of
of  . Then
. Then  , with coprime t and v, fixes some translate of
, with coprime t and v, fixes some translate of  if for every prime p dividing m, there exists an integer i such that
if for every prime p dividing m, there exists an integer i such that  , where
, where 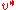 is the exponent (the least common multiple
is the exponent (the least common multiple
of the orders of every element) of the group.
For example, 2 is a multiplier of the (7,3,1)-difference set mentioned above.
 difference family is a set of subsets
difference family is a set of subsets 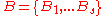 of a group
of a group
 such that the order of
such that the order of  is
is  , the size of
, the size of 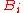 is
is 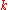 for all
for all 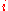 , and every nonidentity element of
, and every nonidentity element of  can be expressed as a product
can be expressed as a product 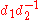 of elements of
of elements of  for some
for some  (i.e. both
(i.e. both 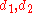 come from the same
come from the same 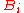 ) in exactly
) in exactly 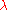 ways.
ways.
A difference set is a difference family with . The parameter equation above generalises to
. The parameter equation above generalises to 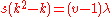 .
.
The development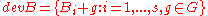 of a difference family is a 2-design.
of a difference family is a 2-design.
Every 2-design with a regular automorphism group is for some difference family
for some difference family 
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a
 difference set is a subset
difference set is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
 of a group
of a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
 such that the order of
such that the order of  is
is  , the size of
, the size of  is
is 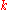 , and every nonidentity element of
, and every nonidentity element of  can be expressed as a product
can be expressed as a product 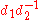 of elements of
of elements of  in exactly
in exactly 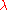 ways.
ways.Basic facts
- A simple counting argument shows that there are exactly
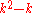 pairs of elements from
pairs of elements from  that will yield nonidentity elements, so every difference set must satisfy the equation
that will yield nonidentity elements, so every difference set must satisfy the equation 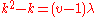 .
. - If
 is a difference set, and
is a difference set, and 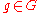 , then
, then 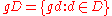 is also a difference set, and is called a translate of
is also a difference set, and is called a translate of  .
. - The set of all translates of a difference set
 forms a symmetric designSymmetric designIn combinatorial mathematics, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points . They are also known as projective designs....
forms a symmetric designSymmetric designIn combinatorial mathematics, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points . They are also known as projective designs....
. In such a design there are elements (mostly called points) and
elements (mostly called points) and  blocks. Each block of the design consists of
blocks. Each block of the design consists of  points, each point is contained in
points, each point is contained in  blocks. Any two blocks have exactly
blocks. Any two blocks have exactly 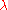 elements in common and any two points are "joined" by
elements in common and any two points are "joined" by 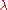 blocks. The group
blocks. The group  then acts as an automorphism group of the design. It is sharply transitive on points and blocks.
then acts as an automorphism group of the design. It is sharply transitive on points and blocks.
- In particular, if
 , then the difference set gives rise to a projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
, then the difference set gives rise to a projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. An example of a (7,3,1) difference set in the group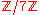 is the subset
is the subset  . The translates of this difference set gives the Fano planeFano planeIn finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
. The translates of this difference set gives the Fano planeFano planeIn finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
.
- In particular, if
- Since every difference set gives a symmetric designSymmetric designIn combinatorial mathematics, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points . They are also known as projective designs....
, the parameter set must satisfy the Bruck–Chowla–Ryser theoremBruck–Chowla–Ryser theoremThe Bruck–Ryser–Chowla theorem is a result on the combinatorics of block designs. It states that if a -design exists with v = b , then:* if v is even, then k − λ is a square;...
. - Not every symmetric designSymmetric designIn combinatorial mathematics, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points . They are also known as projective designs....
gives a difference set.
Multipliers
It has been conjectured that if p is a prime dividing and not dividing v, then the group automorphism defined by
and not dividing v, then the group automorphism defined by  fixes some translate of D. It is known to be true for
fixes some translate of D. It is known to be true for  , and this is known as the First Multiplier Theorem. A more general known result, the Second Multiplier Theorem, first says to choose a divisor
, and this is known as the First Multiplier Theorem. A more general known result, the Second Multiplier Theorem, first says to choose a divisor  of
of  . Then
. Then  , with coprime t and v, fixes some translate of
, with coprime t and v, fixes some translate of  if for every prime p dividing m, there exists an integer i such that
if for every prime p dividing m, there exists an integer i such that  , where
, where 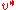 is the exponent (the least common multiple
is the exponent (the least common multipleLeast common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
of the orders of every element) of the group.
For example, 2 is a multiplier of the (7,3,1)-difference set mentioned above.
Parameters
Every difference set known to mankind to this day has one of the following parameters or their complements: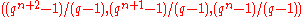 -difference set for some prime power
-difference set for some prime power 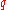 and some positive integer
and some positive integer  .
.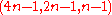 -difference set for some positive integer
-difference set for some positive integer  .
.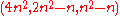 -difference set for some positive integer
-difference set for some positive integer  .
.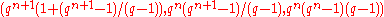 -difference set for some prime power
-difference set for some prime power 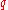 and some positive integer
and some positive integer  .
. -difference set for some positive integer
-difference set for some positive integer  .
.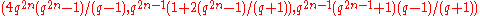 -difference set for some prime power
-difference set for some prime power  and some positive integer
and some positive integer  .
.
Known difference sets
- Singer
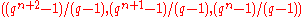 -difference set:
-difference set:
- Let
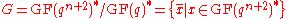 , where
, where 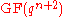 and
and 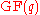 are Galois fields of order
are Galois fields of order 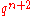 and
and 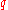 respectively and
respectively and 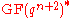 and
and 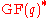 are their respective multiplicative groups of non-zero elements. Then the set
are their respective multiplicative groups of non-zero elements. Then the set 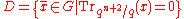 is a
is a 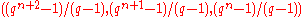 -difference set, where
-difference set, where 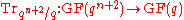 is the trace function
is the trace function  .
.
- Let
Application
It is found by Xia, Zhou and Giannakis that, difference sets can be used to construct a complex vector codebook that achieves the difficult Welch bound on maximum cross correlation amplitude. The so-constructed codebook also forms the so-called Grassmannian manifold.Generalisations
A difference family is a set of subsets
difference family is a set of subsets 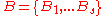 of a group
of a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
 such that the order of
such that the order of  is
is  , the size of
, the size of 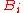 is
is 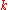 for all
for all 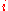 , and every nonidentity element of
, and every nonidentity element of  can be expressed as a product
can be expressed as a product 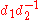 of elements of
of elements of 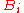 for some
for some 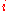 (i.e. both
(i.e. both 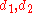 come from the same
come from the same 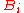 ) in exactly
) in exactly 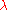 ways.
ways.A difference set is a difference family with
 . The parameter equation above generalises to
. The parameter equation above generalises to 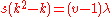 .
.The development
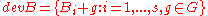 of a difference family is a 2-design.
of a difference family is a 2-design.Every 2-design with a regular automorphism group is
 for some difference family
for some difference family 

