
Arbitrarily varying channel
Encyclopedia
An arbitrarily varying channel (AVC) is a communication channel model used in coding theory
, and was first introduced by Blackwell, Breiman, and Thomasian. This particular channel has unknown parameters that can change over time and these changes may not have a uniform pattern during the transmission of a codeword. uses of this channel can be described using a stochastic matrix
uses of this channel can be described using a stochastic matrix
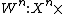
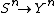 , where
, where  is the input alphabet,
is the input alphabet, 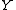 is the output alphabet, and
is the output alphabet, and 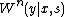 is the probability over a given set of states
is the probability over a given set of states 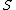 , that the transmitted input
, that the transmitted input  is equal to the received output
is equal to the received output 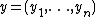 . The state
. The state 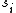 in set
in set 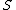 can vary arbitrarily at each time unit
can vary arbitrarily at each time unit 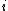 . This channel was developed as an alternative to Shannon's Binary Symmetric Channel
. This channel was developed as an alternative to Shannon's Binary Symmetric Channel
(BSC), where the entire nature of the channel is known, to be more realistic to actual network channel situations.
can vary depending on the certain parameters.
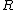 is an achievable rate for a deterministic AVC code if it is larger than
is an achievable rate for a deterministic AVC code if it is larger than  , and if for every positive
, and if for every positive  and
and 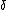 , and very large
, and very large  , length-
, length- block code
block code
s exist that satisfy the following equations: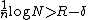 and
and 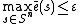 , where
, where 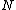 is the highest value in
is the highest value in 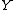 and where
and where  is the average probability of error for a state sequence
is the average probability of error for a state sequence  . The largest rate
. The largest rate 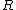 represents the capacity
represents the capacity
of the AVC, denoted by .
.
As you can see, the only useful situations are when the capacity
of the AVC is greater than , because then the channel can transmit a guaranteed amount of data
, because then the channel can transmit a guaranteed amount of data 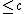 without errors. So we start out with a theorem
without errors. So we start out with a theorem
that shows when is positive in a AVC and the theorem
is positive in a AVC and the theorem
s discussed afterward will narrow down the range
of for different circumstances.
for different circumstances.
Before stating Theorem 1, a few definitions need to be addressed:
Theorem 1: if and only if the AVC is not symmetric. If
if and only if the AVC is not symmetric. If 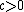 , then
, then 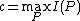 .
.
Proof of 1st part for symmetry: If we can prove that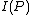 is positive when the AVC is not symmetric, and then prove that
is positive when the AVC is not symmetric, and then prove that 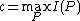 , we will be able to prove Theorem 1. Assume
, we will be able to prove Theorem 1. Assume 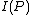 were equal to
were equal to 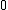 . From the definition of
. From the definition of  , this would make
, this would make 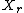 and
and 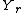 independent random variable
independent random variable
s, for some , because this would mean that neither random variable
, because this would mean that neither random variable
's entropy
would rely on the other random variable
's value. By using equation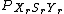 , (and remembering
, (and remembering 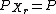 ,) we can get,
,) we can get,
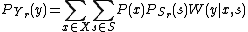
 since
since 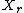 and
and 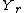 are independent random variable
are independent random variable
s,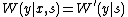 for some
for some 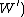
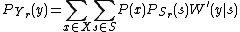
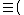 because only
because only 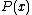 depends on
depends on  now
now
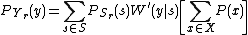
 because
because 
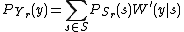
So now we have a probability distribution
on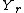 that is independent of
that is independent of 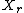 . So now the definition of a symmetric AVC can be rewritten as follows:
. So now the definition of a symmetric AVC can be rewritten as follows: 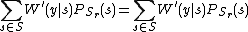 since
since  and
and 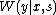 are both functions based on
are both functions based on  , they have been replaced with functions based on
, they have been replaced with functions based on  and
and 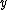 only. As you can see, both sides are now equal to the
only. As you can see, both sides are now equal to the  we calculated earlier, so the AVC is indeed symmetric when
we calculated earlier, so the AVC is indeed symmetric when 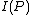 is equal to
is equal to  . Therefore
. Therefore 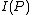 can only be positive if the AVC is not symmetric.
can only be positive if the AVC is not symmetric.
Proof of second part for capacity: See the paper "The capacity of the arbitrarily varying channel revisited: positivity, constraints," referenced below for full proof.
will deal with the capacity
for AVCs with input and/or state constraints. These constraints help to decrease the very large range
of possibilities for transmission and error on an AVC, making it a bit easier to see how the AVC behaves.
Before we go on to Theorem 2, we need to define a few definitions and lemmas
:
For such AVCs, there exists:
Assume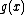 is a given non-negative-valued function on
is a given non-negative-valued function on 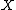 and
and 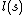 is a given non-negative-valued function on
is a given non-negative-valued function on  and that the minimum values for both is
and that the minimum values for both is 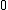 . In the literature I have read on this subject, the exact definitions of both
. In the literature I have read on this subject, the exact definitions of both  and
and 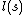 (for one variable
(for one variable 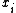 ,) is never described formally. The usefulness of the input constraint
,) is never described formally. The usefulness of the input constraint 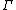 and the state constraint
and the state constraint  will be based on these equations.
will be based on these equations.
For AVCs with input and/or state constraints, the rate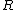 is now limited to codewords of format
is now limited to codewords of format 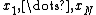 that satisfy
that satisfy 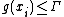 , and now the state
, and now the state  is limited to all states that satisfy
is limited to all states that satisfy 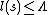 . The largest rate is still considered the capacity
. The largest rate is still considered the capacity
of the AVC, and is now denoted as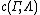 .
.
Lemma 1: Any codes where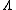 is greater than
is greater than 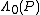 cannot be considered "good" codes, because those kinds of codes have a maximum average probability of error greater than or equal to
cannot be considered "good" codes, because those kinds of codes have a maximum average probability of error greater than or equal to  , where
, where 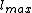 is the maximum value of
is the maximum value of 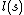 . This isn't a good maximum average error probability because it is fairly large,
. This isn't a good maximum average error probability because it is fairly large, 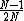 is close to
is close to 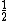 , and the other part of the equation will be very small since the
, and the other part of the equation will be very small since the 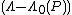 value is squared, and
value is squared, and 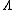 is set to be larger than
is set to be larger than 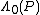 . Therefore it would be very unlikely to receive a codeword without error. This is why the
. Therefore it would be very unlikely to receive a codeword without error. This is why the  condition is present in Theorem 2.
condition is present in Theorem 2.
Theorem 2: Given a positive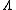 and arbitrarily small
and arbitrarily small 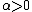 ,
, 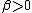 ,
, 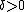 , for any block length
, for any block length 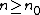 and for any type
and for any type 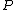 with conditions
with conditions 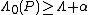 and
and  , and where
, and where 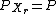 , there exists a code with codewords
, there exists a code with codewords 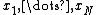 , each of type
, each of type 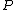 , that satisfy the following equations:
, that satisfy the following equations: 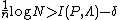 ,
, 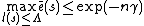 , and where positive
, and where positive 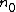 and
and 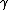 depend only on
depend only on  ,
, 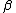 ,
, 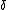 , and the given AVC.
, and the given AVC.
Proof of Theorem 2: See the paper "The capacity of the arbitrarily varying channel revisited: positivity, constraints," referenced below for full proof.
will be for AVCs with randomized
code. For such AVCs the code is a random variable
with values from a family of length-n block code
s, and these codes are not allowed to depend/rely on the actual value of the codeword. These codes have the same maximum and average error probability value for any channel because of its random nature. These types of codes also help to make certain properties of the AVC more clear.
Before we go on to Theorem 3, we need to define a couple important terms first:
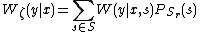
 is very similar to the
is very similar to the 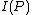 equation mentioned previously,
equation mentioned previously, 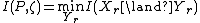 , but now the pmf
, but now the pmf 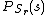 is added to the equation, making the minimum of
is added to the equation, making the minimum of 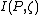 based a new form of
based a new form of 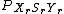 , where
, where  replaces
replaces 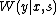 .
.
Theorem 3: The capacity
for randomized
codes of the AVC is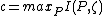 .
.
Proof of Theorem 3: See paper "The Capacities of Certain Channel Classes Under Random Coding" referenced below for full proof.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, and was first introduced by Blackwell, Breiman, and Thomasian. This particular channel has unknown parameters that can change over time and these changes may not have a uniform pattern during the transmission of a codeword.
 uses of this channel can be described using a stochastic matrix
uses of this channel can be described using a stochastic matrixStochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
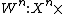
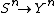 , where
, where  is the input alphabet,
is the input alphabet, 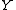 is the output alphabet, and
is the output alphabet, and 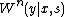 is the probability over a given set of states
is the probability over a given set of states 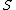 , that the transmitted input
, that the transmitted input  is equal to the received output
is equal to the received output 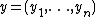 . The state
. The state 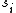 in set
in set 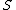 can vary arbitrarily at each time unit
can vary arbitrarily at each time unit 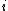 . This channel was developed as an alternative to Shannon's Binary Symmetric Channel
. This channel was developed as an alternative to Shannon's Binary Symmetric ChannelBinary symmetric channel
A binary symmetric channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter wishes to send a bit , and the receiver receives a bit. It is assumed that the bit is usually transmitted correctly, but that it will be "flipped" with a...
(BSC), where the entire nature of the channel is known, to be more realistic to actual network channel situations.
Capacity of deterministic AVCs
An AVC's capacityChannel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
can vary depending on the certain parameters.
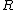 is an achievable rate for a deterministic AVC code if it is larger than
is an achievable rate for a deterministic AVC code if it is larger than  , and if for every positive
, and if for every positive  and
and 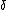 , and very large
, and very large  , length-
, length- block code
block codeBlock code
In coding theory, block codes refers to the large and important family of error-correcting codes that encode data in blocks.There is a vast number of examples for block codes, many of which have a wide range of practical applications...
s exist that satisfy the following equations:
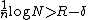 and
and 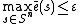 , where
, where 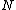 is the highest value in
is the highest value in 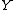 and where
and where  is the average probability of error for a state sequence
is the average probability of error for a state sequence  . The largest rate
. The largest rate 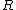 represents the capacity
represents the capacityChannel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
of the AVC, denoted by
 .
.As you can see, the only useful situations are when the capacity
Channel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
of the AVC is greater than
 , because then the channel can transmit a guaranteed amount of data
, because then the channel can transmit a guaranteed amount of data 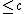 without errors. So we start out with a theorem
without errors. So we start out with a theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
that shows when
 is positive in a AVC and the theorem
is positive in a AVC and the theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s discussed afterward will narrow down the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of
 for different circumstances.
for different circumstances.Before stating Theorem 1, a few definitions need to be addressed:
- An AVC is symmetric if
 for every
for every 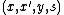 , where
, where 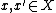 ,
, 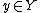 , and
, and 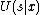 is a channel function
is a channel function 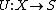 .
. -
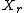 ,
, 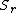 , and
, and 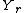 are all random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
are all random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s in sets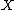 ,
, 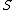 , and
, and 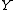 respectively.
respectively. -
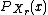 is equal to the probability that the random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is equal to the probability that the random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
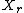 is equal to
is equal to  .
. -
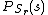 is equal to the probability that the random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is equal to the probability that the random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
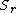 is equal to
is equal to  .
. -
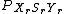 is the combined probability mass functionProbability mass functionIn probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
is the combined probability mass functionProbability mass functionIn probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
(pmf) of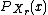 ,
, 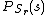 , and
, and 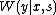 .
. 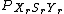 is defined formally as
is defined formally as 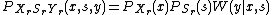 .
. -
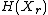 is the entropyInformation entropyIn information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
is the entropyInformation entropyIn information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
of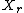 .
. -
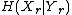 is equal to the average probability that
is equal to the average probability that  will be a certain value based on all the values
will be a certain value based on all the values 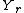 could possibly be equal to.
could possibly be equal to. -
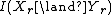 is the mutual informationConditional entropyIn information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
is the mutual informationConditional entropyIn information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
of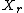 and
and 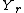 , and is equal to
, and is equal to 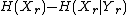 .
. -
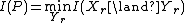 , where the minimum is over all random variables
, where the minimum is over all random variables 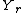 such that
such that 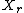 ,
, 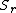 , and
, and  are distributed in the form of
are distributed in the form of 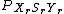 .
.
Theorem 1:
 if and only if the AVC is not symmetric. If
if and only if the AVC is not symmetric. If 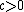 , then
, then 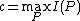 .
.Proof of 1st part for symmetry: If we can prove that
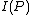 is positive when the AVC is not symmetric, and then prove that
is positive when the AVC is not symmetric, and then prove that 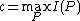 , we will be able to prove Theorem 1. Assume
, we will be able to prove Theorem 1. Assume 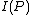 were equal to
were equal to 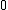 . From the definition of
. From the definition of 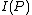 , this would make
, this would make 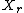 and
and 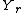 independent random variable
independent random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, for some
 , because this would mean that neither random variable
, because this would mean that neither random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
's entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
would rely on the other random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
's value. By using equation
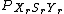 , (and remembering
, (and remembering 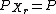 ,) we can get,
,) we can get,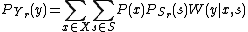
 since
since 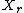 and
and 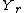 are independent random variable
are independent random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s,
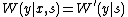 for some
for some 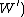
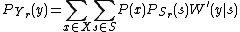
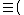 because only
because only 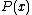 depends on
depends on  now
now
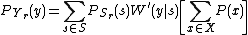
 because
because 
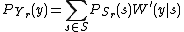
So now we have a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on
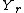 that is independent of
that is independent of 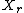 . So now the definition of a symmetric AVC can be rewritten as follows:
. So now the definition of a symmetric AVC can be rewritten as follows: 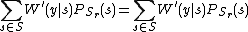 since
since  and
and 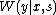 are both functions based on
are both functions based on  , they have been replaced with functions based on
, they have been replaced with functions based on  and
and 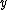 only. As you can see, both sides are now equal to the
only. As you can see, both sides are now equal to the  we calculated earlier, so the AVC is indeed symmetric when
we calculated earlier, so the AVC is indeed symmetric when 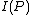 is equal to
is equal to  . Therefore
. Therefore 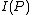 can only be positive if the AVC is not symmetric.
can only be positive if the AVC is not symmetric.Proof of second part for capacity: See the paper "The capacity of the arbitrarily varying channel revisited: positivity, constraints," referenced below for full proof.
Capacity of AVCs with input and state constraints
The next theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
will deal with the capacity
Channel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
for AVCs with input and/or state constraints. These constraints help to decrease the very large range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of possibilities for transmission and error on an AVC, making it a bit easier to see how the AVC behaves.
Before we go on to Theorem 2, we need to define a few definitions and lemmas
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
:
For such AVCs, there exists:
- - An input constraint
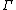 based on the equation
based on the equation 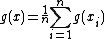 , where
, where  and
and 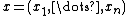 .
. - - A state constraint
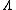 , based on the equation
, based on the equation 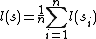 , where
, where 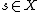 and
and 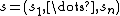 .
. - -
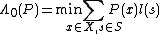
- -
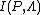 is very similar to
is very similar to 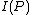 equation mentioned previously,
equation mentioned previously, 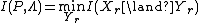 , but now any state
, but now any state  or
or  in the equation must follow the
in the equation must follow the 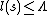 state restriction.
state restriction.
Assume
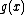 is a given non-negative-valued function on
is a given non-negative-valued function on 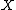 and
and 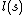 is a given non-negative-valued function on
is a given non-negative-valued function on  and that the minimum values for both is
and that the minimum values for both is 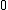 . In the literature I have read on this subject, the exact definitions of both
. In the literature I have read on this subject, the exact definitions of both  and
and 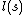 (for one variable
(for one variable 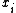 ,) is never described formally. The usefulness of the input constraint
,) is never described formally. The usefulness of the input constraint 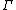 and the state constraint
and the state constraint  will be based on these equations.
will be based on these equations.For AVCs with input and/or state constraints, the rate
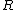 is now limited to codewords of format
is now limited to codewords of format 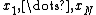 that satisfy
that satisfy 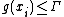 , and now the state
, and now the state  is limited to all states that satisfy
is limited to all states that satisfy 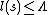 . The largest rate is still considered the capacity
. The largest rate is still considered the capacityChannel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
of the AVC, and is now denoted as
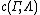 .
.Lemma 1: Any codes where
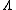 is greater than
is greater than 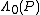 cannot be considered "good" codes, because those kinds of codes have a maximum average probability of error greater than or equal to
cannot be considered "good" codes, because those kinds of codes have a maximum average probability of error greater than or equal to  , where
, where 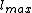 is the maximum value of
is the maximum value of 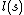 . This isn't a good maximum average error probability because it is fairly large,
. This isn't a good maximum average error probability because it is fairly large, 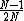 is close to
is close to 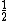 , and the other part of the equation will be very small since the
, and the other part of the equation will be very small since the 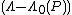 value is squared, and
value is squared, and 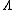 is set to be larger than
is set to be larger than 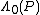 . Therefore it would be very unlikely to receive a codeword without error. This is why the
. Therefore it would be very unlikely to receive a codeword without error. This is why the  condition is present in Theorem 2.
condition is present in Theorem 2.Theorem 2: Given a positive
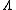 and arbitrarily small
and arbitrarily small 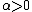 ,
, 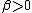 ,
, 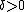 , for any block length
, for any block length 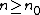 and for any type
and for any type 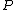 with conditions
with conditions 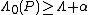 and
and  , and where
, and where 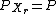 , there exists a code with codewords
, there exists a code with codewords 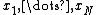 , each of type
, each of type 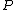 , that satisfy the following equations:
, that satisfy the following equations: 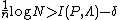 ,
, 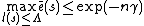 , and where positive
, and where positive 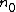 and
and 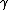 depend only on
depend only on  ,
, 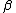 ,
, 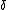 , and the given AVC.
, and the given AVC.Proof of Theorem 2: See the paper "The capacity of the arbitrarily varying channel revisited: positivity, constraints," referenced below for full proof.
Capacity of randomized AVCs
The next theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
will be for AVCs with randomized
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
code. For such AVCs the code is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with values from a family of length-n block code
Block code
In coding theory, block codes refers to the large and important family of error-correcting codes that encode data in blocks.There is a vast number of examples for block codes, many of which have a wide range of practical applications...
s, and these codes are not allowed to depend/rely on the actual value of the codeword. These codes have the same maximum and average error probability value for any channel because of its random nature. These types of codes also help to make certain properties of the AVC more clear.
Before we go on to Theorem 3, we need to define a couple important terms first:
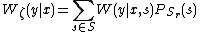
 is very similar to the
is very similar to the 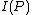 equation mentioned previously,
equation mentioned previously, 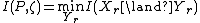 , but now the pmf
, but now the pmf 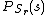 is added to the equation, making the minimum of
is added to the equation, making the minimum of 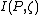 based a new form of
based a new form of 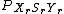 , where
, where  replaces
replaces 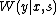 .
.Theorem 3: The capacity
Channel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
for randomized
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
codes of the AVC is
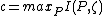 .
.Proof of Theorem 3: See paper "The Capacities of Certain Channel Classes Under Random Coding" referenced below for full proof.
See also
- Binary symmetric channelBinary symmetric channelA binary symmetric channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter wishes to send a bit , and the receiver receives a bit. It is assumed that the bit is usually transmitted correctly, but that it will be "flipped" with a...
- Binary erasure channelBinary erasure channelA binary erasure channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter sends a bit , and the receiver either receives the bit or it receives a message that the bit was not received...
- Z-channel (information theory)Z-channel (information theory)A Z-channel is a communications channel used in coding theory and information theory to model the behaviour of some data storage systems.- Definition :...
- Channel model
- Information theoryInformation theoryInformation theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
- Coding theoryCoding theoryCoding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...

