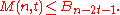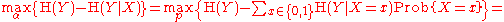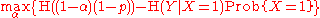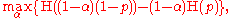Z-channel (information theory)
Encyclopedia
A Z-channel is a communications channel used in coding theory
and information theory
to model the behaviour of some data storage systems.
s describing the probability distributions of the input and the output of the channel, respectively, then the crossovers of the channel are characterized by the conditional probabilities
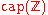of the Z-channel 
with the crossover 1 → 0 probability p, when the input random variable X is distributed according to the geometric distribution with probability α for the occurrence of 0, is calculated as follows.
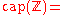
where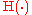
is the binary entropy function.
The maximum is attained for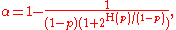
yielding the following value of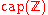
as a function of p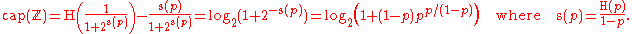
For small p, the capacity is approximated by
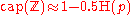
as compared to the capacity
of the binary symmetric channel
with crossover probability p.
on the words 
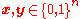of length n transmitted via a Z-channel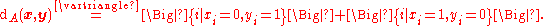
Define the sphere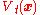
of radius t around a word 
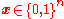of length n as the set of all the words at distance t or less from 
, in other words,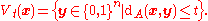
A code
of length n is said to be t-asymmetric-error-correcting if for any two codewords 
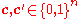, one has 
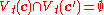. Denote by 
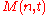the maximum size of a t-asymmetric-error-correcting code of length n.
The Varshamov bound.
For n≥1 and t≥1,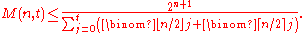
Let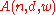
denote the maximal number of binary vectors of length n of weight w and with Hamming distance at least d apart.
The constant-weight code bound.
For n > 2t ≥ 2, let the sequence B0, B1, ..., Bn-2t-1 be defined as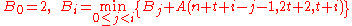
for 
.
Then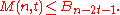
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
to model the behaviour of some data storage systems.
Definition
A Z-channel (or a binary asymmetric channel) is a channel with binary input and binary output where the crossover 1 → 0 occurs with nonnegative probability p whereas the crossover 0 ← 1 never occurs. In other words, if X and Y are the random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s describing the probability distributions of the input and the output of the channel, respectively, then the crossovers of the channel are characterized by the conditional probabilities
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
- Prob{Y = 0 | X = 0} = 1
- Prob{Y = 0 | X = 1} = p
- Prob{Y = 1 | X = 0} = 0
- Prob{Y = 1 | X = 1} = 1−p
Capacity
The capacityChannel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
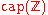of the Z-channel with the crossover 1 → 0 probability p, when the input random variable X is distributed according to the geometric distribution with probability α for the occurrence of 0, is calculated as follows.
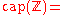
where
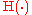is the binary entropy function.The maximum is attained for
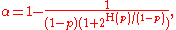
yielding the following value of
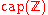as a function of p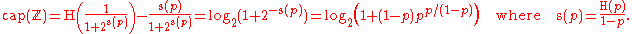For small p, the capacity is approximated by
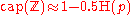
as compared to the capacity
of the binary symmetric channelBinary symmetric channel
A binary symmetric channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter wishes to send a bit , and the receiver receives a bit. It is assumed that the bit is usually transmitted correctly, but that it will be "flipped" with a...
with crossover probability p.
Bounds on the size of an asymmetric-error-correcting code
Define the following distance function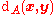 on the words 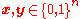of length n transmitted via a Z-channel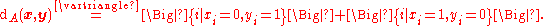Define the sphere
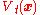of radius t around a word 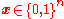of length n as the set of all the words at distance t or less from , in other words,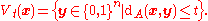A code
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
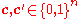of length n is said to be t-asymmetric-error-correcting if for any two codewords , one has 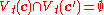. Denote by 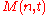the maximum size of a t-asymmetric-error-correcting code of length n.The Varshamov bound.
For n≥1 and t≥1,
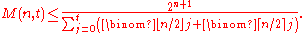
Let
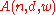denote the maximal number of binary vectors of length n of weight w and with Hamming distance at least d apart.The constant-weight code bound.
For n > 2t ≥ 2, let the sequence B0, B1, ..., Bn-2t-1 be defined as
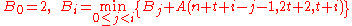for .Then