Binary symmetric channel
Encyclopedia
A binary symmetric channel (or BSC) is a common communications channel model used in coding theory
and information theory
. In this model, a transmitter wishes to send a bit
(a zero or a one), and the receiver receives a bit. It is assumed that the bit is usually transmitted
correctly, but that it will be "flipped" with a small probability
(the "crossover probability"). This channel is used frequently in information theory because it is one of the simplest channels to analyze.
This channel is often used by theorists because it is one of the simplest noisy channels to analyze. Many problems in communication theory
can be reduced
to a BSC. Conversely, being able to transmit effectively over the BSC can give rise to solutions for more complicated channels.
, is a channel with binary input and binary output and probability of error p; that is, if X is the transmitted random variable
and Y the received variable, then the channel is characterized by the conditional probabilities
It is assumed that 0 ≤ p ≤ 1/2. If p > 1/2, then the receiver can swap the output (interpret 1 when it sees 0, and vice versa) and obtain an equivalent channel with crossover probability 1 − p ≤ 1/2.
is 1 − H(p), where H(p) is the binary entropy function.
The converse can be shown by a sphere packing
argument. Given a codeword, there are roughly 2n H(p) typical
output sequences. There are 2n total possible outputs, and the input chooses from a codebook
of size 2nR. Therefore, the receiver would choose to partition
the space into "spheres" with 2n / 2nR = 2n(1 − R) potential outputs each. If R > 1 − H(p), then the spheres will be packed too tightly asymptotically
and the receiver will not be able to identify the correct codeword with vanishing probability.
from 
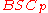as "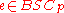
". The noise 
is essentially a random variable
with each of its indexes being a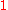
with probability 
and a 
with probability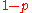 
.
Theorem 1
For al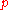l
< 
and all 
such that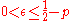 
, there exists a pair of encoding
and decoding
functions
: 
and 
: 
respectively, and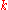 
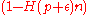
such that every message 
has the following property: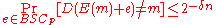 
for a sufficient large integer 
.
What this theorem actually implies is, a message when picked from
, encoded with a random encoding function 
, and send across a noisy 
, there is a very high probability of recovering the original message by decoding, if 
or in effect the rate of the channel is bounded by the quantity stated in the theorem. The decoding error probability is exponentially small.
We shall now prove Theorem 1 .
Proof
We shall first describe the encoding function
and the decoding function 
used in the theorem. Its good to state here that we would be using the probabilistic method
to prove this theorem. Shannon's theorem was one of the earliest applications of this method.
Encoding function
: The encoding function 
: 
is selected at random. This means, given any message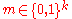 
, we choose 
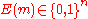uniformly and independently at random.
Decoding function
: The decoding function 
: 
is given any received codeword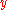 
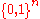, we find the message 
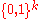such that 
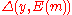is minimum (with ties broken arbitrarily). This kind of a decoding function is called a maximum likelihood decoding (MLD) function.
Now first we show, for a fixe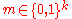d
and 
chosen randomly, the probability of failure over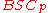 
noise is exponentially small. At this point, the proof works for a fixed message 
. Next we extend this result to work for all 
. We achieve this by eliminating half of the codewords from the code with the argument that the proof for the decoding error probability holds for at least half of the codewords. The latter method is called expurgation. This gives the total process the name random coding with expurgation.
A high level proof: Given a fixed message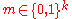
, we need to estimate the expected value
of the probability
of the received codeword along with the noise does not give back
on decoding. That is to say, we need to estimate: 
.
Let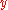
be the received codeword. In order for the decoded codeword 
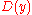not to be equal to the message 
, one of the following events must occur:
We can apply Chernoff bound
to ensure the non occurrence of the first event. By applying Chernoff bound
we have,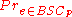
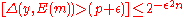. Thus, for any 
, we can pick 
to be large enough to make the above probability exponentially small.
As for the second event, we note that the probability that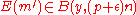
is 
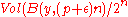where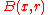 
is the Hamming ball of radius 
centered at vector 
and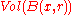 
is its volume. Using approximation to estimate the number of codewords in the Hamming ball, we have 
. Hence the above probability amounts to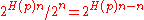 
. Now using union bound, we can upper bound the existence of such an 
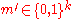by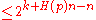 
which is 
, as desired by the choice of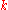 
.
A detailed proof: From the above analysis, we calculate the probability of the event that the decoded codeword plus the channel noise is not the same as the original message sent. We shall introduce some symbols here. Let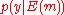
denote the probability of receiving codeword 
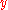given that codeword 
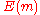was sent. Denote 
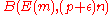by 
.
We get the last inequality by our analysis using the Chernoff bound
above. Now taking expectation on both sides we have,
[
[
] 
.
.
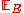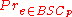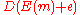
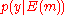Now we have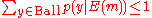
. This just says, that the quantity 
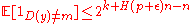, again from the analysis in the higher level proof above. Hence, taking everything together we have
, by appropriately choosing the value of 
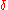. Since the above bound holds for each message, we have 
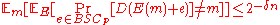. Now we can change the order of summation in the expectation with respect to the message and the choice of the encoding function 
, without loss of generality. Hence we have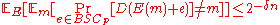 
. Hence in conclusion, by probabilistic method, we have some encoding function 
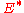and a corresponding decoding function 
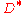such that 
.
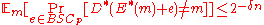At this point, the proof works for a fixed message
. But we need to make sure that the above bound holds for all the messages 
simultaneously. For that, let us sort the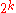 
messages by their decoding error probabilities. Now by applying Markov's inequality
, we can show the decoding error probability for the first
messages to be at most 
. Thus in order to confirm that the above bound to hold for every message 
, we could just trim off the last 
messages from the sorted order. This essentially gives us another encoding function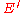 
with a corresponding decoding function 
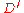with a decoding error probability of at most 
with the same rate. Taking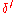 
to be equal to 
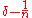we bound the decoding error probability to 
. This expurgation process completes the proof of Theorem 1.
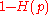is the best rate one can achieve over a binary symmetric channel. Formally the theorem states:
Theorem 2
If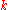
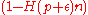
then the following is true for every encoding
and decoding
function
: 
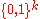
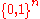and 
: 
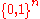
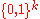respectively: 
[
.
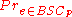For a detailed proof of this theorem, the reader is asked to refer to the bibliography. The intuition behind the proof is however showing the number of errors to grow rapidly as the rate grows beyond the channel capacity. The idea is the sender generates messages of dimension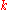
, while the channel 
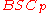introduces transmission errors. When the capacity of the channel is 
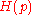, the number of errors is typically 
for a code of block length 
. The maximum number of messages is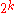 
. The output of the channel on the other hand has 
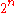possible values. If there is any confusion between any two messages, it is likely that 
. Hence we would have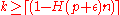 
, a case we would like to avoid to keep the decoding error probability exponentially small.
The approach behind the design of codes which meet the channel capacities of
, 
have been to correct a lesser number of errors with a high probability, and to achieve the highest possible rate. Shannon’s theorem gives us the best rate which could be achieved over a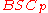 
, but it does not give us an idea of any explicit codes which achieve that rate. In fact such codes are typically constructed to correct only a small fraction of errors with a high probability, but achieve a very good rate. The first such code was due to George D. Forney in 1966. The code is a concatenated code by concatenating two different kinds of codes. We shall discuss the construction Forney's code for the Binary Symmetric Channel and analyze its rate and decoding error probability briefly here. Various explicit codes for achieving the capacity of the binary erasure channel
have also come up recently.
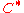
to achieve the capacity of Theorem 1 for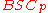 
. In his code,
For the outer code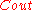
, a Reed-Solomon code would have been the first code to have come in mind. However, we would see that the construction of such a code cannot be done in polynomial time. This is why a binary linear code is used for 
.
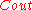For the inner code code
we find a linear code
by exhaustively searching from the linear code
of block length
and dimension 
, whose rate meets the capacity of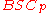 
, by Theorem 1.
The rate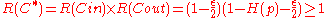
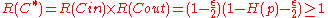
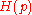
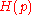
which almost meets the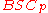 
capacity. We further note that the encoding and decoding of 
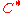can be done in polynomial time with respect to 
. As a matter of fact, encoding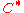 
takes time 
. Further, the decoding algorithm described takes time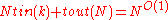 
as long as 
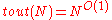; and 
.
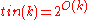is to:
Note that each block of code for
is considered a symbol for 
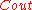. Now since the probability of error at any index 
for 
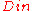is at most 
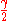and the errors in 
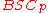are independent, the expected number of errors for 
is at most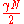 
by linearity of expectation. Now applying Chernoff bound
, we have bound error probability of more than
errors occurring to be 
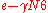. Since the outer code 
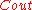can correct at most 
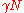errors, this is the decoding
error probability of
. This when expressed in asymptotic terms, gives us an error probability of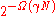 
. Thus the achieved decoding error probability of 
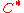is exponentially small as Theorem 1.
We have given a general technique to construct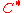
. For more detailed descriptions on 
and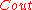 
please read the following references. Recently a few other codes have also being constructed for achieving the capacities. Its worth mentioning that LDPC codes are now being considered for this purpose for their faster decoding time. Please refer to the book by Richardson and Urbanke cited in the reference to know more about such codes.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. In this model, a transmitter wishes to send a bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
(a zero or a one), and the receiver receives a bit. It is assumed that the bit is usually transmitted
Data transmission
Data transmission, digital transmission, or digital communications is the physical transfer of data over a point-to-point or point-to-multipoint communication channel. Examples of such channels are copper wires, optical fibres, wireless communication channels, and storage media...
correctly, but that it will be "flipped" with a small probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
(the "crossover probability"). This channel is used frequently in information theory because it is one of the simplest channels to analyze.
Description
The BSC is a binary channel; that is, it can transmit only one of two symbols (usually called 0 and 1). (A non-binary channel would be capable of transmitting more than 2 symbols, possibly even an infinite number of choices.) The transmission is not perfect, and occasionally the receiver gets the wrong bit.This channel is often used by theorists because it is one of the simplest noisy channels to analyze. Many problems in communication theory
Communication theory
Communication theory is a field of information and mathematics that studies the technical process of information and the human process of human communication.- History :- Origins :...
can be reduced
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
to a BSC. Conversely, being able to transmit effectively over the BSC can give rise to solutions for more complicated channels.
Definition
A binary symmetric channel with crossover probability p denoted by, is a channel with binary input and binary output and probability of error p; that is, if X is the transmitted random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
and Y the received variable, then the channel is characterized by the conditional probabilities
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
- Pr( Y = 0 | X = 0 ) = 1 − p
- Pr( Y = 0 | X = 1) = p
- Pr( Y = 1 | X = 0 ) = p
- Pr( Y = 1 | X = 1 ) = 1 − p
It is assumed that 0 ≤ p ≤ 1/2. If p > 1/2, then the receiver can swap the output (interpret 1 when it sees 0, and vice versa) and obtain an equivalent channel with crossover probability 1 − p ≤ 1/2.
Capacity of BSCp
The capacity of the channelChannel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
is 1 − H(p), where H(p) is the binary entropy function.
The converse can be shown by a sphere packing
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
argument. Given a codeword, there are roughly 2n H(p) typical
Typical set
In information theory, the typical set is a set of sequences whose probability is close to two raised to the negative power of the entropy of their source distribution. That this set has total probability close to one is a consequence of the asymptotic equipartition property which is a kind of law...
output sequences. There are 2n total possible outputs, and the input chooses from a codebook
Codebook
A codebook is a type of document used for gathering and storing codes. Originally codebooks were often literally books, but today codebook is a byword for the complete record of a series of codes, regardless of physical format.-Cryptography:...
of size 2nR. Therefore, the receiver would choose to partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
the space into "spheres" with 2n / 2nR = 2n(1 − R) potential outputs each. If R > 1 − H(p), then the spheres will be packed too tightly asymptotically
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
and the receiver will not be able to identify the correct codeword with vanishing probability.
Shannon's channel capacity theorem for BSCp
Shannon's noisy coding theorem is general for all kinds of channels. We consider a special case of this theorem for a binary symmetric channel with an error probability p.Noisy coding theorem for BSCp
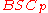We denote (and would continue to denote) noise from as "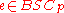". The noise is essentially a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with each of its indexes being a
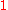with probability and a with probability 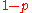.Theorem 1
For all
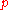< and all such that 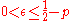, there exists a pair of encodingCode
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
and decoding
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
functions
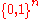
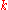
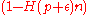
: and : respectively, and such that every message has the following property: 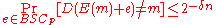for a sufficient large integer .What this theorem actually implies is, a message when picked from
, encoded with a random encoding function , and send across a noisy , there is a very high probability of recovering the original message by decoding, if or in effect the rate of the channel is bounded by the quantity stated in the theorem. The decoding error probability is exponentially small.We shall now prove Theorem 1 .
Proof
We shall first describe the encoding function
and the decoding function used in the theorem. Its good to state here that we would be using the probabilistic methodProbabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
to prove this theorem. Shannon's theorem was one of the earliest applications of this method.
Encoding function
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
: The encoding function : is selected at random. This means, given any message 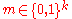, we choose 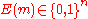uniformly and independently at random.Decoding function
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
: The decoding function : is given any received codeword 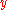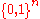, we find the message 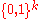such that 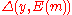is minimum (with ties broken arbitrarily). This kind of a decoding function is called a maximum likelihood decoding (MLD) function.Now first we show, for a fixed
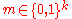and chosen randomly, the probability of failure over 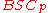noise is exponentially small. At this point, the proof works for a fixed message . Next we extend this result to work for all . We achieve this by eliminating half of the codewords from the code with the argument that the proof for the decoding error probability holds for at least half of the codewords. The latter method is called expurgation. This gives the total process the name random coding with expurgation.A high level proof: Given a fixed message
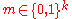, we need to estimate the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of the received codeword along with the noise does not give back
on decoding. That is to say, we need to estimate: .Let
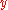be the received codeword. In order for the decoded codeword 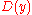not to be equal to the message , one of the following events must occur:-
does not lie within the Hamming ball of radius 
for any 
greater than 
, centered at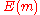 
. This condition is mainly used to make the calculations easier.
- There is another message
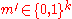such that 
. In other words the errors due to noise take the transmitted codeword closer to another encoded message.
We can apply Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
to ensure the non occurrence of the first event. By applying Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
we have,
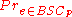
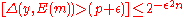. Thus, for any , we can pick to be large enough to make the above probability exponentially small.As for the second event, we note that the probability that
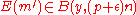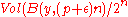is where 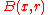is the Hamming ball of radius centered at vector and 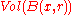is its volume. Using approximation to estimate the number of codewords in the Hamming ball, we have . Hence the above probability amounts to 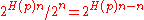. Now using union bound, we can upper bound the existence of such an 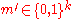by 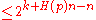which is , as desired by the choice of 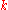.A detailed proof: From the above analysis, we calculate the probability of the event that the decoded codeword plus the channel noise is not the same as the original message sent. We shall introduce some symbols here. Let
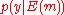denote the probability of receiving codeword 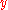given that codeword 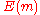was sent. Denote 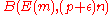by .We get the last inequality by our analysis using the Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
above. Now taking expectation on both sides we have,
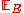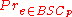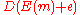
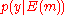[[ ] ..Now we have
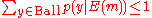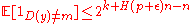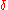. This just says, that the quantity , again from the analysis in the higher level proof above. Hence, taking everything together we have, by appropriately choosing the value of . Since the above bound holds for each message, we have 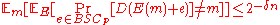. Now we can change the order of summation in the expectation with respect to the message and the choice of the encoding function , without loss of generality. Hence we have 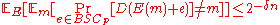. Hence in conclusion, by probabilistic method, we have some encoding function 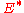and a corresponding decoding function 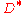such that 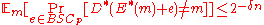.At this point, the proof works for a fixed message
. But we need to make sure that the above bound holds for all the messages simultaneously. For that, let us sort the 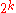messages by their decoding error probabilities. Now by applying Markov's inequalityMarkov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
, we can show the decoding error probability for the first
messages to be at most . Thus in order to confirm that the above bound to hold for every message , we could just trim off the last messages from the sorted order. This essentially gives us another encoding function 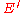with a corresponding decoding function 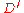with a decoding error probability of at most with the same rate. Taking 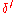to be equal to 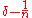we bound the decoding error probability to . This expurgation process completes the proof of Theorem 1.Converse of Shannon's capacity theorem
The converse of the capacity theorem essentially states that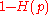 is the best rate one can achieve over a binary symmetric channel. Formally the theorem states:Theorem 2
If
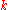
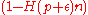
then the following is true for every encodingCode
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
and decoding
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
function
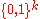
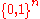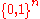
: and : 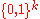respectively: 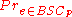[ .For a detailed proof of this theorem, the reader is asked to refer to the bibliography. The intuition behind the proof is however showing the number of errors to grow rapidly as the rate grows beyond the channel capacity. The idea is the sender generates messages of dimension
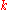, while the channel 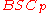introduces transmission errors. When the capacity of the channel is 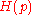, the number of errors is typically for a code of block length . The maximum number of messages is 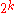. The output of the channel on the other hand has 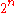possible values. If there is any confusion between any two messages, it is likely that . Hence we would have 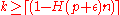, a case we would like to avoid to keep the decoding error probability exponentially small.Codes for BSCp
Very recently, a lot of work has been done and is also being done to design explicit error-correcting codes to achieve the capacities of several standard communication channels. The motivation behind designing such codes is to relate the rate of the code with the fraction of errors which it can correct.The approach behind the design of codes which meet the channel capacities of
, have been to correct a lesser number of errors with a high probability, and to achieve the highest possible rate. Shannon’s theorem gives us the best rate which could be achieved over a 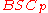, but it does not give us an idea of any explicit codes which achieve that rate. In fact such codes are typically constructed to correct only a small fraction of errors with a high probability, but achieve a very good rate. The first such code was due to George D. Forney in 1966. The code is a concatenated code by concatenating two different kinds of codes. We shall discuss the construction Forney's code for the Binary Symmetric Channel and analyze its rate and decoding error probability briefly here. Various explicit codes for achieving the capacity of the binary erasure channelBinary erasure channel
A binary erasure channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter sends a bit , and the receiver either receives the bit or it receives a message that the bit was not received...
have also come up recently.
Forney's code for BSCp
Forney constructed a concatenated code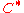 to achieve the capacity of Theorem 1 for 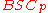. In his code,- The outer code
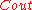is a code of block length 
and rate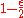 
over the field 
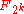, and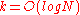 
. Additionally, we have a decodingCodeA code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
algorithm
for 
which can correct up to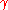 
fraction of worst case errors and runs in 
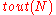time. - The inner code
is a code of block length 
, dimension 
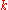, and a rate of 
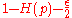. Additionally, we have a decoding algorithm 
for 
with a decodingCodeA code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
error probability of at most
over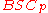 
and runs in 
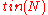time.
For the outer code
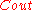, a Reed-Solomon code would have been the first code to have come in mind. However, we would see that the construction of such a code cannot be done in polynomial time. This is why a binary linear code is used for 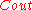.For the inner code code
we find a linear codeLinear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
by exhaustively searching from the linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
of block length
and dimension , whose rate meets the capacity of 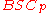, by Theorem 1.The rate
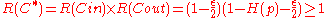
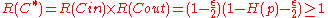
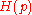
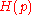
which almost meets the 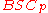capacity. We further note that the encoding and decoding of 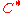can be done in polynomial time with respect to . As a matter of fact, encoding 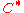takes time . Further, the decoding algorithm described takes time 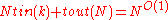as long as 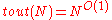; and 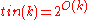.Decoding error probability for C*
A natural decoding algorithm for is to:- Assume
- Execute
on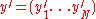 
Note that each block of code for
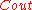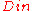is considered a symbol for . Now since the probability of error at any index for is at most 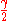and the errors in 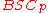are independent, the expected number of errors for is at most 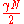by linearity of expectation. Now applying Chernoff boundChernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
, we have bound error probability of more than
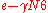errors occurring to be . Since the outer code 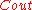can correct at most 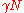errors, this is the decodingCode
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
error probability of
. This when expressed in asymptotic terms, gives us an error probability of 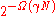. Thus the achieved decoding error probability of 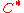is exponentially small as Theorem 1.We have given a general technique to construct
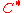. For more detailed descriptions on and 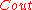please read the following references. Recently a few other codes have also being constructed for achieving the capacities. Its worth mentioning that LDPC codes are now being considered for this purpose for their faster decoding time. Please refer to the book by Richardson and Urbanke cited in the reference to know more about such codes.