
Dirac equation in the algebra of physical space
Encyclopedia
The Dirac equation
, as the relativistic
equation that describes
spin 1/2 particles in quantum mechanics
can be written in terms of the Algebra of physical space
(APS), which is a case of a Clifford algebra
or geometric algebra
that is based in the use of paravectors.
The Dirac equation in APS, including the electromagnetic interaction, reads

Another form of the Dirac equation in terms of the Space time algebra was given earlier by David Hestenes
.
In general, the Dirac equation in the formalism of geometric algebra has the advantage of
providing a direct geometric interpretation.

such that the representation of the spinor in terms of the Pauli matrices is

The standard form of the Dirac equation can be recovered by decomposing the spinor in its right and left-handed
spinor components, which are extracted with the help of the projector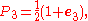
such that

with the following matrix representation

The Dirac equation can be also written as
Without electromagnetic interaction, the following equation is obtained from
the two equivalent forms of the Dirac equation
so that
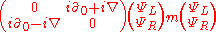
or in matrix representation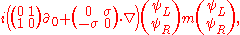
where the second column of the right and left spinors can be dropped by defining the
single column chiral spinors as

The standard relativistic covariant form of the Dirac equation in the Weyl
representation can be easily identified
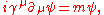
such that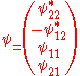
Given two spinors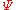 and
and  in APS and
in APS and
their respective spinors in the standard form as and
and
 , one can verify the following identity
, one can verify the following identity ,
,
such that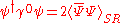
on the Spinor of the type
so that the kinetic term of the Dirac equation transforms as
where we identify the following rotation
The mass term transforms as
so that we can verify the invariance of the form of the Dirac equation.
A more demanding requirement is that the Dirac equation should be
invariant under a local gauge transformation of the type
In this case, the kinetic term transforms as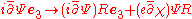 ,
,
so that the left side of the Dirac equation transforms covariantly as
where we identify the need to perform an electromagnetic gauge transformation.
The mass term transforms as in the case with global rotation, so, the form
of the Dirac equation remains invariant.

which satisfies the continuity equation


 and positive energy
and positive energy  is
is

This solution is unimodular
and the current resembles the classical proper velocity
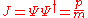
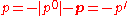 is
is

This solution is anti-unimodular
and the current resembles the classical proper velocity

but with a remarkable feature: "the time runs backwards"
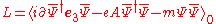
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
, as the relativistic
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
equation that describes
spin 1/2 particles in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
can be written in terms of the Algebra of physical space
Algebra of physical space
In physics, the algebra of physical space is the use of the Clifford or geometric algebra Cℓ3 of the three-dimensional Euclidean space as a model for -dimensional space-time, representing a point in space-time via a paravector .The Clifford algebra Cℓ3 has a faithful representation, generated by...
(APS), which is a case of a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
or geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
that is based in the use of paravectors.
The Dirac equation in APS, including the electromagnetic interaction, reads

Another form of the Dirac equation in terms of the Space time algebra was given earlier by David Hestenes
David Hestenes
David Orlin Hestenes, Ph.D. is a physicist. For more than 30 years, he was employed in the Department of Physics and Astronomy of Arizona State University , where he retired with the rank of Research Professor and is now emeritus....
.
In general, the Dirac equation in the formalism of geometric algebra has the advantage of
providing a direct geometric interpretation.
Relation with the standard form
The spinor can be written in a null basis as
such that the representation of the spinor in terms of the Pauli matrices is


The standard form of the Dirac equation can be recovered by decomposing the spinor in its right and left-handed
spinor components, which are extracted with the help of the projector
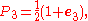
such that


with the following matrix representation


The Dirac equation can be also written as

Without electromagnetic interaction, the following equation is obtained from
the two equivalent forms of the Dirac equation

so that
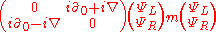
or in matrix representation
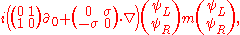
where the second column of the right and left spinors can be dropped by defining the
single column chiral spinors as


The standard relativistic covariant form of the Dirac equation in the Weyl
representation can be easily identified
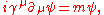
such that
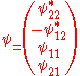
Given two spinors
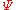 and
and  in APS and
in APS andtheir respective spinors in the standard form as
 and
and , one can verify the following identity
, one can verify the following identity ,
,such that
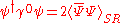
Electromagnetic gauge
The Dirac equation is invariant under a global right rotation appliedon the Spinor of the type

so that the kinetic term of the Dirac equation transforms as

where we identify the following rotation

The mass term transforms as

so that we can verify the invariance of the form of the Dirac equation.
A more demanding requirement is that the Dirac equation should be
invariant under a local gauge transformation of the type

In this case, the kinetic term transforms as
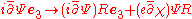 ,
,so that the left side of the Dirac equation transforms covariantly as

where we identify the need to perform an electromagnetic gauge transformation.
The mass term transforms as in the case with global rotation, so, the form
of the Dirac equation remains invariant.
Current
The current is defined as
which satisfies the continuity equation

Second order Dirac equation
An application of the Dirac equation on itself leads to the second order Dirac equation
Positive energy solutions
A solution for the free particle with momentum and positive energy
and positive energy  is
is
This solution is unimodular

and the current resembles the classical proper velocity

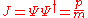
Negative energy solutions
A solution for the free particle with negative energy and momentum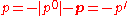 is
is
This solution is anti-unimodular

and the current resembles the classical proper velocity


but with a remarkable feature: "the time runs backwards"

Dirac Lagrangian
The Dirac Lagrangian is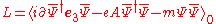
Textbooks
- Baylis, William (2002). Electrodynamics: A Modern Geometric Approach (2nd ed.). Birkhäuser. ISBN 0-8176-4025-8
- W. E. Baylis, editor, Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering, Birkhäuser, Boston 1996.
Articles
- Baylis, William, Classical eigenspinors and the Dirac equation, Phys. Rev. A 45, 4293–4302 (1992)
- HestenesDavid HestenesDavid Orlin Hestenes, Ph.D. is a physicist. For more than 30 years, he was employed in the Department of Physics and Astronomy of Arizona State University , where he retired with the rank of Research Professor and is now emeritus....
D., Observables, operators, and complex numbers in the Dirac theory, J. Math. Phys.Journal of Mathematical PhysicsThe Journal of Mathematical Physics is a peer-reviewed journal published monthly by the American Institute of Physics devoted to the publication of papers in mathematical physics. The journal was first published bimonthly beginning in January 1960; it became a monthly publication in 1963. The...
16, 556 (1975)

