ADM formalism
Encyclopedia
The ADM Formalism developed in 1959 by Richard Arnowitt
, Stanley Deser
and Charles W. Misner
is a Hamiltonian
formulation of general relativity
. This formulation plays an important role both in quantum gravity
and numerical relativity
.
A comprehensive review of this formalism was published by the same authors in "Gravitation: An introduction to current research" Louis Witten
(editor), Wiley NY (1962); chapter 7, pp 227–265. Recently, this has been reprinted in the journal General Relativity and Gravitation
The original papers can be found in Physical Review
archives.
is foliated
into a family of spacelike surfaces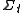
, labeled by their time coordinate 
, and with coordinates on each slice given by 
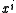. The dynamic variables of this theory are taken to be the metric tensor
of three dimensional spatial slices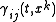
and their conjugate momenta
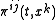. Using these variables it is possible to define a Hamiltonian
, and thereby write the equations of motion for general relativity in the form of Hamilton's equations.
In addition to the twelve variables
and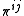 
, there are four Lagrange multipliers
: the lapse function,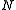
, and components of shift vector field, 
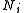. These describe how each of the "leaves" 
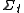of the foliation of spacetime are welded together. The equations of motion for these variables can be freely specified; this freedom corresponds to the freedom to specify how to lay out the coordinate system in space and time.
and the metric tensor for the full four-dimensional spacetime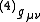 
.
The text here uses Einstein notation
in which summation over repeated indices is assumed.
Two types of derivatives are used: Partial derivative
s are denoted either by the operator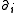
or by subscripts preceded by a comma. Covariant derivative
s are denoted either by the operator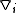
or by subscripts preceded by a semicolon.
The determinant
of the metric tensor is represented by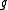
(with no indices). Other tensor symbols written without indices represent the trace of the corresponding tensor such as 
.
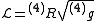
which is a product of the determinant
of the four-dimensional metric tensor
for the full spacetime and its Ricci scalar
. This is the Lagrangian from the Einstein-Hilbert action
.
The desired outcome of the derivation is to define an embedding of three-dimensional spatial slices in the four-dimensional spacetime. The metric of the three-dimensional slices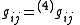
will be the generalized coordinates
for a Hamiltonian formulation. The conjugate momenta can then be computed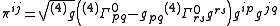
using standard techniques and definitions. The symbols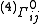
are Christoffel symbols
associated with the metric of the full four-dimensional spacetime. The lapse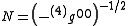
and the shift vector
are the remaining elements of the four-metric tensor.
Having identified the quantities for the formulation, the next step is to rewrite the Lagrangian in terms of these variables. The new expression for the Lagrangian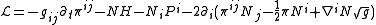
is conveniently written in terms of the two new quantities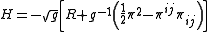
and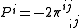
which are known as the Hamiltonian constraint
and the momentum constraint respectively. Note also that the lapse and the shift appear in the Hamiltonian as Lagrange multipliers
.
on three-dimensional spaces embedded in the four-dimensional spacetime
, it is possible and desirable to use the usual procedures from Lagrangian mechanics
to derive "equations of motion" that describe the time evolution of both the metric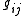
and its conjugate momentum 
. The result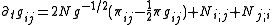
and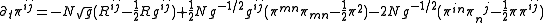
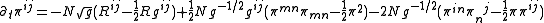
is a non-linear set of partial differential equations.
Taking variations with respect to the lapse and shift provide constraint equations
and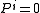
and the lapse and shift themselves can be freely specified, reflecting the fact that coordinate systems can be freely specified in both space and time.
, in the same way that one constructs the Schrödinger equation
corresponding to a given Hamiltonian in quantum mechanics
. That is, replace the canonical momenta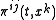
and the spatial metric functions by linear functional differential operators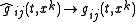
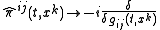
More precisely, the replacing of classical variables by operators is restricted by commutation relations
. The hats represents operators in quantum theory.
This leads to the Wheeler-deWitt equation
.
. In order to find other solutions, there is an active field of study known as numerical relativity
in which supercomputers are used to find approximate solutions to the equations. In order to construct such solutions numerically, most researchers start with a formulation of the Einstein equations closely related to the ADM formulation. The most common approaches start with an initial value problem
based on the ADM formalism.
In Hamiltonian formulations, the basic point is replacement of set of second order equations by another first order set of equations. We may get this second set of equations by Hamiltonian formulation in an easy way. Of course this is very useful for numerical physics, because the reduction of order of differential equations must be done, if we want to prepare equations for a computer.
in general relativity
which is only applicable to some special geometries of spacetime
that asymptotically approach a well-defined metric tensor
at infinity — for example a spacetime that asymptotically approaches Minkowski space
. The ADM energy in these cases is defined as a function of the deviation of the metric tensor from its prescribed asymptotic form. In other words, the ADM energy is computed as the strength of the gravitational field at infinity.
The quantity is also called the ADM Hamiltonian, especially if one finds a different formula than the definition above that however leads to the same result.
If the required asymptotic form is time-independent (such as the Minkowski space itself), then it respects the time-translational symmetry
. Noether's theorem
then implies that the ADM energy is conserved. According to general relativity, the conservation law for the total energy does not hold in more general, time-dependent backgrounds - for example, it is completely violated in physical cosmology
. Cosmic inflation
in particular is able to produce energy (and mass) from "nothing" because the vacuum energy
density is roughly constant, but the volume of the Universe grows exponentially
.
Richard Arnowitt
Richard Lewis Arnowitt is an American physicist known for his contributions to theoretical particle physics and to general relativity.Arnowitt is a Distinguished Professor at Texas A&M University, where he is a member of the Department of Physics....
, Stanley Deser
Stanley Deser
Stanley Deser is an American physicist known for his contributions to general relativity. Currently, he is the Ancell Professor of Physics at Brandeis University in Waltham, Massachusetts....
and Charles W. Misner
Charles W. Misner
Charles W. Misner is an American physicist and one of the authors of Gravitation. His specialties include general relativity and cosmology. His work has also provided early foundations for studies of quantum gravity and numerical relativity....
is a Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
formulation of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. This formulation plays an important role both in quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
and numerical relativity
Numerical relativity
Numerical relativity is one of the branches of general relativity that uses numerical methods and algorithms to solve and analyze problems. To this end, supercomputers are often employed to study black holes, gravitational waves, neutron stars and many other phenomena governed by Einstein's Theory...
.
A comprehensive review of this formalism was published by the same authors in "Gravitation: An introduction to current research" Louis Witten
Louis Witten
Louis Witten is an American theoretical physicist and the father of Edward Witten.Witten's research has centered around classical gravitation, including the discovery of certain exact electrovacuum solutions to the Einstein field equation...
(editor), Wiley NY (1962); chapter 7, pp 227–265. Recently, this has been reprinted in the journal General Relativity and Gravitation
General Relativity and Gravitation
General Relativity and Gravitation is a monthly, peer reviewed scientific journal. It was established in 1970, and is published by Springer on behalf of the International Society on General Relativity and Gravitation. The two editors in chief are G.F.R. Ellis and H. Nicolai...
The original papers can be found in Physical Review
Physical Review
Physical Review is an American scientific journal founded in 1893 by Edward Nichols. It publishes original research and scientific and literature reviews on all aspects of physics. It is published by the American Physical Society. The journal is in its third series, and is split in several...
archives.
Overview
The formalism supposes that spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is foliated
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
into a family of spacelike surfaces
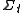, labeled by their time coordinate , and with coordinates on each slice given by 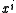. The dynamic variables of this theory are taken to be the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
of three dimensional spatial slices
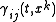and their conjugate momentaCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
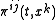. Using these variables it is possible to define a HamiltonianHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, and thereby write the equations of motion for general relativity in the form of Hamilton's equations.
In addition to the twelve variables
and 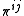, there are four Lagrange multipliersLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
: the lapse function,
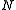, and components of shift vector field, 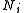. These describe how each of the "leaves" 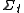of the foliation of spacetime are welded together. The equations of motion for these variables can be freely specified; this freedom corresponds to the freedom to specify how to lay out the coordinate system in space and time.Notation
Most references adopt notation in which four dimensional tensors are written in abstract index notation, and that Greek indices are spacetime indices taking values (0, 1, 2, 3) and Latin indices are spatial indices taking values (1, 2, 3). In the derivation here, a superscript (4) is prepended to quantities that typically have both a three-dimensional and a four-dimensional version, such as the metric tensor for three-dimensional slices and the metric tensor for the full four-dimensional spacetime 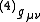.The text here uses Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
in which summation over repeated indices is assumed.
Two types of derivatives are used: Partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s are denoted either by the operator
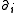or by subscripts preceded by a comma. Covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s are denoted either by the operator
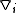or by subscripts preceded by a semicolon.The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the metric tensor is represented by
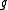(with no indices). Other tensor symbols written without indices represent the trace of the corresponding tensor such as .Lagrangian Formulation
The starting point for the ADM formulation is the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
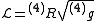
which is a product of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the four-dimensional metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
for the full spacetime and its Ricci scalar
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
. This is the Lagrangian from the Einstein-Hilbert action
Einstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
.
The desired outcome of the derivation is to define an embedding of three-dimensional spatial slices in the four-dimensional spacetime. The metric of the three-dimensional slices
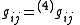
will be the generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
for a Hamiltonian formulation. The conjugate momenta can then be computed
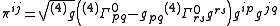
using standard techniques and definitions. The symbols
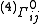are Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
associated with the metric of the full four-dimensional spacetime. The lapse
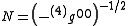
and the shift vector
are the remaining elements of the four-metric tensor.
Having identified the quantities for the formulation, the next step is to rewrite the Lagrangian in terms of these variables. The new expression for the Lagrangian
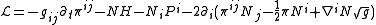
is conveniently written in terms of the two new quantities
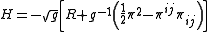
and
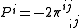
which are known as the Hamiltonian constraint
Hamiltonian constraint
In loop quantum gravity, dynamics such as time-evolutions of fields are controlled by the Hamiltonian constraint. The identity of the Hamiltonian constraint is a major open question in quantum gravity, as is extracting of physical observables from any such specific constraint.The Thiemann operator...
and the momentum constraint respectively. Note also that the lapse and the shift appear in the Hamiltonian as Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
.
Equations of Motion
Although the variables in the Lagrangian represent the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
on three-dimensional spaces embedded in the four-dimensional spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, it is possible and desirable to use the usual procedures from Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
to derive "equations of motion" that describe the time evolution of both the metric
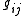and its conjugate momentum . The result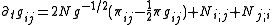and
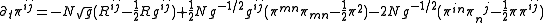
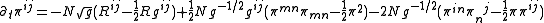
is a non-linear set of partial differential equations.
Taking variations with respect to the lapse and shift provide constraint equations
and
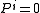
and the lapse and shift themselves can be freely specified, reflecting the fact that coordinate systems can be freely specified in both space and time.
Application to Quantum Gravity
Using the ADM formulation, it is possible to attempt to construct a quantum theory of gravityQuantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
, in the same way that one constructs the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
corresponding to a given Hamiltonian in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. That is, replace the canonical momenta
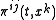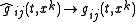
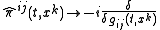
and the spatial metric functions by linear functional differential operatorsMore precisely, the replacing of classical variables by operators is restricted by commutation relations
Canonical commutation relation
In physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...
. The hats represents operators in quantum theory.
This leads to the Wheeler-deWitt equation
Wheeler-deWitt equation
In theoretical physics, the Wheeler–DeWitt equation is a functional differential equation. It is ill defined in the general case, but very important in theoretical physics, especially in quantum gravity. It is a functional differential equation on the space of three dimensional spatial metrics...
.
Application to Numerical Solutions of the Einstein Equations
There are relatively few exact solutions to the Einstein field equationsEinstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
. In order to find other solutions, there is an active field of study known as numerical relativity
Numerical relativity
Numerical relativity is one of the branches of general relativity that uses numerical methods and algorithms to solve and analyze problems. To this end, supercomputers are often employed to study black holes, gravitational waves, neutron stars and many other phenomena governed by Einstein's Theory...
in which supercomputers are used to find approximate solutions to the equations. In order to construct such solutions numerically, most researchers start with a formulation of the Einstein equations closely related to the ADM formulation. The most common approaches start with an initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
based on the ADM formalism.
In Hamiltonian formulations, the basic point is replacement of set of second order equations by another first order set of equations. We may get this second set of equations by Hamiltonian formulation in an easy way. Of course this is very useful for numerical physics, because the reduction of order of differential equations must be done, if we want to prepare equations for a computer.
ADM Energy
ADM energy is a special way to define the energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
which is only applicable to some special geometries of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
that asymptotically approach a well-defined metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
at infinity — for example a spacetime that asymptotically approaches Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. The ADM energy in these cases is defined as a function of the deviation of the metric tensor from its prescribed asymptotic form. In other words, the ADM energy is computed as the strength of the gravitational field at infinity.
The quantity is also called the ADM Hamiltonian, especially if one finds a different formula than the definition above that however leads to the same result.
If the required asymptotic form is time-independent (such as the Minkowski space itself), then it respects the time-translational symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
then implies that the ADM energy is conserved. According to general relativity, the conservation law for the total energy does not hold in more general, time-dependent backgrounds - for example, it is completely violated in physical cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
. Cosmic inflation
Cosmic inflation
In physical cosmology, cosmic inflation, cosmological inflation or just inflation is the theorized extremely rapid exponential expansion of the early universe by a factor of at least 1078 in volume, driven by a negative-pressure vacuum energy density. The inflationary epoch comprises the first part...
in particular is able to produce energy (and mass) from "nothing" because the vacuum energy
Vacuum energy
Vacuum energy is an underlying background energy that exists in space even when the space is devoid of matter . The concept of vacuum energy has been deduced from the concept of virtual particles, which is itself derived from the energy-time uncertainty principle...
density is roughly constant, but the volume of the Universe grows exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
.
See also
- Canonical coordinatesCanonical coordinatesIn mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
- Canonical gravity
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Wheeler-deWitt equationWheeler-deWitt equationIn theoretical physics, the Wheeler–DeWitt equation is a functional differential equation. It is ill defined in the general case, but very important in theoretical physics, especially in quantum gravity. It is a functional differential equation on the space of three dimensional spatial metrics...