Absolute presentation of a group
Encyclopedia
In mathematics
, one method of defining a group
is by an absolute presentation.
Recall that to define a group
by means of a presentation
, one specifies a set
of generators
so that every element of the group can be written as a product of some of these generators, and a set
of relations among those generators. In symbols:
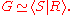
Informally
is the group generated by the set 
such that 
for all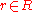 
. But here there is a tacit assumption that 
is the "freest" such group as clearly the relations are satisfied in any homomorphic
image of
. One way of being able to eliminate this tacit assumption is by specifying that certain words in 
should not be equal to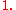 
That is we specify a set 
, called the set of irrelations, such that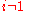 
for all 
.
one specifies a set 
of generators, a set 
of relations among those generators and a set 
of irrelations among those
generators. We then say
has absolute presentation
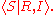
provided that:
A more algebraic, but equivalent, way of stating condition 2 is:
Remark: The concept of an absolute presentation has been fruitful in fields such as algebraically closed group
s and the Grigorchuk topology.
In the literature, in a context where absolute presentations are being discussed, a normal presentation is sometimes referred to as a relative presentation. The term seems rather strange as one may well ask "relative to what?" and the only justification seems to be that relative is habitually used as an antonym
to absolute.
of order 8 has the presentation
But, up to isomorphism there are three more groups that "satisfy" the relation
namely:
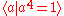
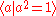and
However none of these satisfy the irrelation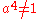
. So an absolute presentation for the cyclic group of order 8 is: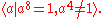
It is part of the definition of an absolute presentation that the irrelations are not satisfied in any proper homomorphic image of the group. Therefore:
Is not an absolute presentation for the cyclic group of order 8 because the irrelation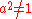
is satisfied in the cyclic group of order 4.
's study of the isomorphism problem
for algebraically closed group
s.
A common strategy for considering whether two groups
and 
are isomorphic is to consider whether a presentation for one might be transformed into a presentation for the other. However algebraically closed groups are neither finitely generated nor recursively presented
and so it is impossible to compare their presentations. Neumann considered the following alternative strategy:
Suppose we know that a group
with finite presentation 
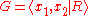can be embedded in the algebraically closed group 
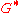then given another algebraically closed group 
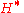, we can ask "Can 
be embedded in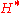 
?"
It soon becomes apparent that a presentation for a group does not contain enough information to make this decision for while there may be a homomorphism
, this homomorphism need not be an embedding. What is needed is a specification for 
that "forces" any homomorphism preserving that specification to be an embedding. An absolute presentation does precisely this.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, one method of defining a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is by an absolute presentation.
Recall that to define a group
by means of a presentationPresentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
, one specifies a set
of generatorsGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
so that every element of the group can be written as a product of some of these generators, and a set
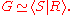
of relations among those generators. In symbols:Informally
is the group generated by the set such that for all 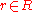. But here there is a tacit assumption that is the "freest" such group as clearly the relations are satisfied in any homomorphicHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
image of
. One way of being able to eliminate this tacit assumption is by specifying that certain words in should not be equal to 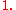That is we specify a set , called the set of irrelations, such that 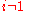for all .Formal Definition
To define an absolute presentation of a group one specifies a set of generators, a set of relations among those generators and a set of irrelations among thosegenerators. We then say
has absolute presentation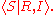provided that:
-
has presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
- Given any homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
such that the irrelations 
are satisfied in 
, 
is isomorphic to 
.
A more algebraic, but equivalent, way of stating condition 2 is:
- 2a. if
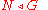is a non-trivial normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of
then 
Remark: The concept of an absolute presentation has been fruitful in fields such as algebraically closed group
Algebraically closed group
In mathematics, in the realm of group theory, a group A\ is algebraically closed if any finite set of equations and inequations that "make sense" in A\ already have a solution in A\...
s and the Grigorchuk topology.
In the literature, in a context where absolute presentations are being discussed, a normal presentation is sometimes referred to as a relative presentation. The term seems rather strange as one may well ask "relative to what?" and the only justification seems to be that relative is habitually used as an antonym
Antonym
In lexical semantics, opposites are words that lie in an inherently incompatible binary relationship as in the opposite pairs male : female, long : short, up : down, and precede : follow. The notion of incompatibility here refers to the fact that one word in an opposite pair entails that it is not...
to absolute.
Example
The cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 8 has the presentation
But, up to isomorphism there are three more groups that "satisfy" the relation
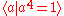
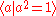namely: andHowever none of these satisfy the irrelation
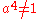. So an absolute presentation for the cyclic group of order 8 is: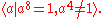It is part of the definition of an absolute presentation that the irrelations are not satisfied in any proper homomorphic image of the group. Therefore:
Is not an absolute presentation for the cyclic group of order 8 because the irrelation
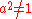is satisfied in the cyclic group of order 4.Background
The notion of an absolute presentation arises from Bernhard NeumannBernhard Neumann
Bernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
's study of the isomorphism problem
Isomorphism problem
Isomorphism problem may refer to:* graph isomorphism problem* group isomorphism problem...
for algebraically closed group
Algebraically closed group
In mathematics, in the realm of group theory, a group A\ is algebraically closed if any finite set of equations and inequations that "make sense" in A\ already have a solution in A\...
s.
A common strategy for considering whether two groups
and are isomorphic is to consider whether a presentation for one might be transformed into a presentation for the other. However algebraically closed groups are neither finitely generated nor recursively presentedPresentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
and so it is impossible to compare their presentations. Neumann considered the following alternative strategy:
Suppose we know that a group
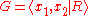with finite presentation can be embedded in the algebraically closed group 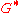then given another algebraically closed group 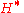, we can ask "Can be embedded in 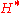?"It soon becomes apparent that a presentation for a group does not contain enough information to make this decision for while there may be a homomorphism
, this homomorphism need not be an embedding. What is needed is a specification for that "forces" any homomorphism preserving that specification to be an embedding. An absolute presentation does precisely this.